A 540 kg car is merging onto the interstate on a banked curve. The curve is banked 7.1o from the horizontal and is rated at 35 mph. The car takes the turn at 52 mph (23 m/s). What sideways frictional force is required between the car and the road in order for the car to stay in its lane? The radius of the curve is 210 m.
-
In this problem, you are asked to relate motion (the car moves in a circle) to force (friction). Force and motion of a single object are always related through Newton’s Second Law, so this is a force or 2nd Law problem.
Even if no forces were mentioned, and you were asked, for example, for the degree to which the curve is banked, you know that it takes a net inward force to make an object move in a circle and so forces are the appropriate interactions to consider.
-
Step 1
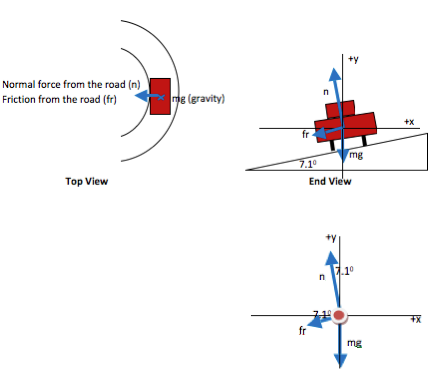
Your FBD is not yet finished, because tension has both x- and y- components. Continue down to step 2 when you are ready to continue.
----------------------------------------------------------------------------------------------
Step 2
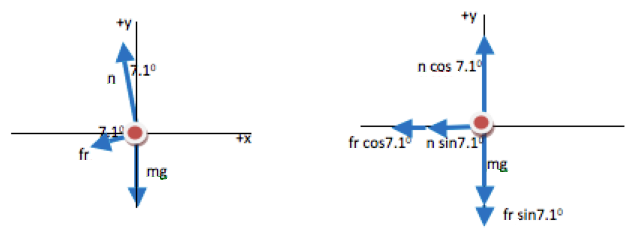
In the final FBD drawn here, all forces are divided into components. The contribution each force makes in the x-direction (in the plane of the circle) is shown explicitly, as is the contribution each force makes in the y-direction. The FBD is now a visual representation of ∑F=ma in each direction.
Can this problem be worked using rotational kinematics?
No. Rotational kinematics is appropriate if you wish to describe the motion around the circle, but it does not provide information about the cause of that motion.
Why isn’t velocity shown on the figure?
The free body diagram is a sketch of the forces on an object, or the causes of motion. Velocity will allow you to calculate the inward acceleration due to those forces and therefore does not show up on the FBD. It will make an appearance in the equation.
Why didn’t you choose the x-axis to be along the incline?
The math to solve a 2nd Law problem is always easier if you pick one axis along the direction of acceleration. That way, one component of a is zero and you generally have fewer linked equations. In order to go in a circle, you know that you need an inward acceleration equal to v2/r. In this case, inward means horizontally in. If acceleration is inward along the incline, the car will slide out of its lane. Therefore, you want to pick a coordinate system with one axis horizontally inward and not along the incline to match the actual direction of a.
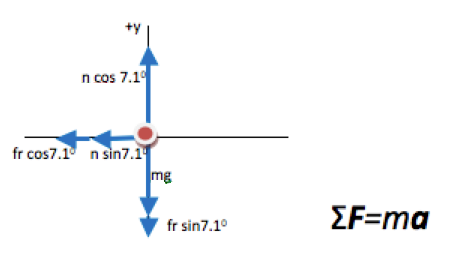
How did you know where to put the 7.1o angle for normal force and friction?
The easiest way to know where to put the 7.1o angles on your FBD is look at the small and large angles on your drawing. In other words, 7.1o is less than half of a right angle, so draw the slope of the incline to be very small. Then you can see that n makes a smaller angle with the +y axis than it does with the -x axis, and the smaller angle is 7.1o. Likewise, fr makes a smaller angle with the –x axis than it does with the –y axis.
How do you divide normal force into its components?
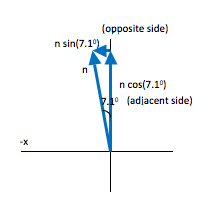
As you can see in the figure, the x- and y-components of a vector make up the sides of a right triangle. The vector itself forms the hypotenuse (h). The side of the triangle opposite the angle that you use is given by h sinθ and the side that touches the angle you use is given by h cosθ (soh cah toa)
In this case, the y-component of n is adjacent to the 7.10angle and so is given by n cos(7.1o) as shown. Likewise, the x-component is opposite to the 7.1o angle and is therefore given by n sin (7.1o).How do you divide friction into its components?
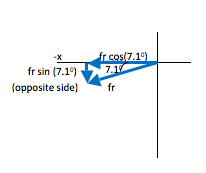
As you can see in the figure, the x- and y-components of a vector make up the sides of a right triangle. The vector itself forms the hypotenuse (h). The side of the triangle opposite the angle that you use is given by h sinθ and the side that touches the angle you use is given by h cosθ (soh cah toa)
In this case, the x-component of fr is adjacent to the 7.1oangle and so is given by fr cos(7.1o) as shown. Likewise, the y-component is opposite to the 7.1o angle and is therefore given by fr sin (7.1o).I don’t get the same answer as you. Are my numbers close enough?
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
Note that in this problem a small difference in truncation makes a very large difference in the answer, so as long as you approached the problem correctly don’t worry too much about the numbers.If a road is banked, or built so that outer side of the lane is higher than the inner, then the normal force between the car and the road (and perpendicular to the road) has a component which pushes inward on the car. Remember than an inward force is required in order to make an object move in a circle. At the “rated speed,” the inward component of normal force is enough to push the car around in a circle—no sideways friction between the tires and the road is required. (It is of course true that most real curves are not exactly circles and so the rated speed isn’t exactly the same throughout, unless the degree to which the road is banked also changes.)
Friction always acts along a surface and opposes sliding motion across the surface. In this case, the car is traveling too fast for the curve. You know from experience that the faster you go the more force you need to turn. This shows up as v in v2/r—a faster speed requires a greater inward acceleration. It can also be understood through inertia—the faster the car moves, the greater its inertia (to continue in a straight line) and so the greater the force needed to cause a given change to its motion. Whichever way you best understand friction in this case, you can see that is must be directed inward along the incline in order to help pull the car inward around the curve and to oppose sliding outward.
The math to solve a 2nd Law problem is always easier if you pick one axis along the direction of acceleration. That way, one component of a is zero and you generally have fewer linked equations. In order to go in a circle, you know that you need an inward acceleration equal to v2/r. In this case, inward means horizontally in. If acceleration is inward along the incline, the car will slide out of its lane. Therefore, you want to pick a coordinate system with one axis horizontally inward and not along the incline to match the actual direction of a.
The easiest way to know where to put the 7.1o angles on your FBD is look at the small and large angles on your drawing. In other words, 7.1o is less than half of a right angle, so draw the slope of the incline to be very small. Then you can see that n makes a smaller angle with the +y axis than it does with the -x axis, and the smaller angle is 7.1o. Likewise, fr makes a smaller angle with the –x axis than it does with the –y axis.
Even though the top view of the car on the road shows the circular nature of the motion, it is not a useful view for showing the forces. Gravity acts straight down, friction acts down along the incline, and normal force acts out from the incline. You can see the forces and their components if you draw an end view instead.

As you can see in the figure, the x- and y-components of a vector make up the sides of a right triangle. The vector itself forms the hypotenuse (h). The side of the triangle opposite the angle that you use is given by h sinθ and the side that touches the angle you use is given by h cosθ (soh cah toa)
In this case, the y-component of n is adjacent to the 7.10angle and so is given by n cos(7.1o) as shown. Likewise, the x-component is opposite to the 7.1o angle and is therefore given by n sin (7.1o).
As you can see in the figure, the x- and y-components of a vector make up the sides of a right triangle. The vector itself forms the hypotenuse (h). The side of the triangle opposite the angle that you use is given by h sinθ and the side that touches the angle you use is given by h cosθ (soh cah toa)
In this case, the x-component of fr is adjacent to the 7.1oangle and so is given by fr cos(7.1o) as shown. Likewise, the y-component is opposite to the 7.1o angle and is therefore given by fr sin (7.1o).As the picture is drawn in this problem, the inside of the curve is to the left which I chose to be the –x direction. Therefore, acceleration and the x-components of normal force and friction are all to the left and so are all negative.
Note that the negative sign is for acceleration and not for v. Therefore, it does not get squared and so when I multiplied each term in the x-equation by -1, all terms became positive.Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
Note that in this problem a small difference in truncation makes a very large difference in the answer, so as long as you approached the problem correctly don’t worry too much about the numbers.Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
Both friction and normal force have components in the negative x direction.
The cos component of normal force acts in the positive y direction. Gravity and the vertical component of friction both act down, or in the negative direction.
-
The key equation for any problem that relates forces and motion is Newton’s Second Law. Regardless of what quantity you are asked to find, begin with the Second Law. If additional information is needed, it will become apparent as you proceed.
-
Step 1
At this point, it seems that you have two equations and two unknowns (fr and n). Scroll down to continue the mathematical solution.
----------------------------------------------------------------------------------------------
Step 2
At this stage in the problem, we have two unknowns, n and fr, and two unsolved equations:
fr cos(7.1o) + n sin(7.1o) = 1360 N
n cos(7.1o) – 5290 N – fr sin(7.1o) = 0
One approach that always works is to solve one equation for one of the variables and substitute it into the other.
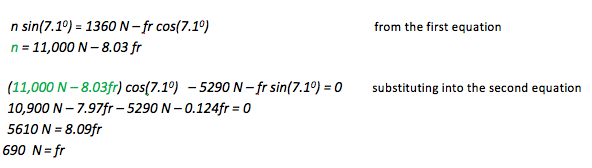
Friction is the only unknown quantity that was requested in this problem. No further mathematical solution is necessary.
Why isn’t velocity included on the free body diagram?
The free body diagram is a stylized drawing to help you visualize the cause of acceleration, and to directly map the drawing into the left hand side (ΣF) of Newton’s Second Law. Velocity allows you to calculate the inward acceleration, which is the effect of the forces.
Why didn’t you pick the x-axis to be along the incline?
The math is always easier if you pick one axis along the direction of acceleration. That way, one component of a is zero and you generally have fewer linked equations. In order to go in a circle, you know that you need an inward acceleration equal to v2/r. In this case, inward means horizontally in. If acceleration is inward along the incline, the car will slide out of its lane.
What does it mean that the “banked curve” is “rated at” a given speed?
If a road is banked, or built so that outer side of the lane is higher than the inner, then the normal force between the car and the road pushes inward on the car. Remember than an inward force is required in order to make an object move in a circle. At the “rated speed,” the inward component of normal force is enough to push the car around in a circle—no sideways friction between the tires and the road is required. (It is of course true that most real curves are not exactly circles and so the rated speed isn’t exactly the same throughout, unless the degree to which the road is banked also changes.)
Why isn’t there air resistance?
There is! However, when you drive a car at a constant velocity you must apply the gas. In other words, you have a forward force from the tires which balances any resistive forces on the car. You could show both of those forces (which would be in the z-direction, or along the road) and that they cancel to zero if you like.
Why isn’t buoyant force included on the free body diagram?
It is true that air puts a small buoyant force on the car. However, the size of the upward buoyant force compared to the downward force of gravity is very small. (The ratio of the two is given by the ratio of the density of air to the density of car.) So to the number of significant figures included in this problem, we do not need to take buoyant force into account.
No. Rotational kinematics is appropriate if you wish to describe the motion around the circle, but it does not provide information about the cause of that motion.
The free body diagram is a sketch of the forces on an object, or the causes of motion. Acceleration is the effect of those forces and therefore does not show up on the FBD. It will make an appearance in the equation.the cause of that motion.
-
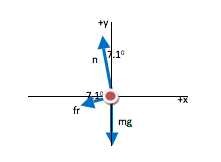
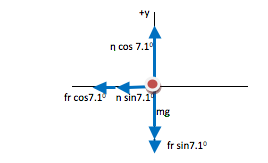
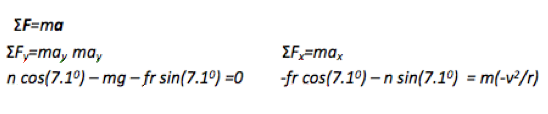
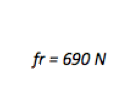
In this problem, a car is traveling in a circle on a banked incline. The normal force not only balances against gravity (as seen in the y-equation) but also pushes the car inward around the circle (as seen in the x-equation.)
Because the car is traveling faster than the rated speed, normal force is not enough to keep the car moving in a circle. If there was no friction present, the car would move outward in the curve (up along the incline.) If friction is present, therefore, it will act to prevent the tires from sliding out. In other words, friction will act in along the incline. The x-component of friction, then, provides additional force to keep the car in its circular path.
