A laser shines through a double slit apparatus forming a pattern of dots on a screen 1.5 m away. The two slits are 0.10 mm apart and the dots on the screen are 8.3 mm . What color is the laser light?
-
You might immediately recognize this as an interference problem because of the reference to a double slit apparatus. However, it is worth recognizing the deeper underlying physics. If you think about the reason for the bright and dark spots, you will realize that the dots form a standing wave pattern due to the interference of rays of light from each opening.
As you can see in the picture below, light diffracts when it passes through each slit and so rays of light radiate out as if each slit was a source of light. The two rays that reach any single point on the screen (such as is indicated by the red dot on the drawing) interfere constructively to give a dot of light or destructively to leave a dark, or unlit, region on the screen.
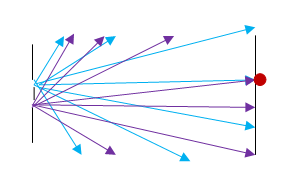
An interference pattern is a type of standing wave pattern. It results when two or more identical waves (waves of the same wavelength and amplitude) are in the same place at the same time. If there is a location in which the waves are always out of phase, the waves will always cancel at that location and there will not be any wave present. In the case of light waves shining on a screen, this would be a location where the screen is unlit. Any location in which the waves are always in phase will result addition of the waves and a bright spot on the screen. As a result, the standing wave pattern on the screen will be a series of bright dots or lines separated by unlit sections.
As waves go through openings or around barriers, they spread out as if those openings or barriers were the source of the wave. This is called diffraction and results in diverging rays and circular wave fronts. In the case of a double slit apparatus, the incoming wave encounters a screen with two very narrow openings. The openings are so narrow that you can work the problem as if a single ray leaves the opening in any given direction.
Aren't the bright spots crests and the dark spots troughs?
No. As light propogates, a series of crests and troughs come to your eye. It is this variation in the electric and magnetic fields that causes your eye to perceive light. You do not see alternating light and dark as crests and troughs propgate to your eye.
Isn't this just a definition problem? Can't I just plug into the interference equation and be done?
It is true that there is a single equation that maps to double slit interference problems. However, if you take the time to understand the problem well you will see that "double slit interference patterns" are just one more example of standing waves and reflect the same physics as all other standing wave problems. In addition, in this case you need to consider the geometry of the experiment because the information you are given is not one of the variables in the equation. So a picture is required here to fully understand the information provided.
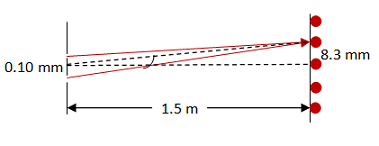
To picture the experimental set up in the problem, first locate the double slit apparatus and the screen. It may also help to draw dots of light and dark on the screen so you can visualize the interference pattern. Then draw the two interfering rays that reach the point you need to consider. Finallly, the dotted lines on the drawing will help you understand the geometry that is used to define angles and locations.
Why don't you show the waves themselves?
As discussed further with selection of an equation, whether a particular location is a bright spot or a dark spot depends on the path difference between the rays of light. I could certainly draw light waves instead of rays, but it complicates the picture and makes it harder to see the paths.
Light is incident on the double slit apparatus and rays spread out from each opening. Information about the distance between the openings will be needed as you work the problem. In this case, you are told the openings are 0.10 mm apart.
The screen is just a wall, piece of paper, or any other surface on which the light shines. Because the rays of light intefer constructively in some places and destructively in others, there will be areas of light on the screen separated by unlit areas. Although you do not need to draw this resulting interference pattern, it is very useful to do so. One of the main areas of confusion with double slit intereference pattern problems is the meaning of m in the equation. Drawing the pattern helps you to visualize m.
In this problem, you are told about distances (to the screen, between the dots.) However, bright and dark spots are located in interference equations by angle instead. The reason for that choice is that regardless of the distance to the screen, any angle will yield the same result (always dark or always bright along that line of sight.) By definition, Θ is the angle between the line bisecting, and perpendicular to, the double slit apparatus and the line from the center of the apparatus to the location of interest--shown as the two dashed lines in the drawing.
The distance to the screen is the distance between the double slit apparatus and the location at which you view the pattern.

Whenever a standing wave pattern comes about because of double slit interference, bright spots and unlit spots can be located according to the equations
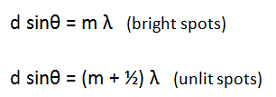
The problem asks me to find color. How does this equation relate to color?
Your eye sees different wavelengths as different colors. λ is the symbol used for wavelength.
How do these equations relate to interference? I don't see the connection to constructive and destructive interference of waves.
Take a look at the blue triangle in the drawing below. If you drop a line down from the top opening perpendicular to the bottom ray, you have drawn the arc of a circle centered around the bright spot you are considering. The remaining part of the rays, then, are the same length. So the base of the blue triangle represents the path difference between the two rays. In other words, light from the bottom opening travels farther than light from the top opening by the amount shown in blue.
Remember that the rays come from a single wave incident on the double slit barrier. In other words, the two rays start out in phase. If one of the rays travels some whole number of wavelengths further than the other (if the blue line is equal to an integer number of wavelengths), the waves are once again in phase. Waves of the same phase add constructively--they give a bright spot. If the blue line (path difference) is a whole number of wavelengths plus an additional half wavelength longer, the waves will be out of phase and add desctructively. They will cancel out. All of this understanding is represented in the right hand side of the equations. m is an integer, and so the right hand sides of the equations represent path differences that are whole, or whole plus half, wavelengths.
The left hand side of the equations also represents path difference. d sinθ comes from the blue triangle. d is the hypotenuse of the triangle (note that for very small angles, sine and tangent are approximately the same) and the angle θ of the figure in your drawing is the same as the top angle of the triangle.
m is an integer. It plays two related roles. First, it numbers the dots on the screen. The bright spot straight down the middle is m =0. The first bright spot on either side of that "central maximum" is labeled by m =1; the second bright spot on each side by m =2; etc. Similarly, the first dark spot on each side is also numbered by m =0 (so that m + 1/2 = 1/2); the second on each side my m =1 (so that m + 1/2 = 1.5) and so forth. For some reason, this is the most confusing part of using these formulas. It is truly worth drawing the diffraction pattern on your drawing and labeling the dots as shown below.
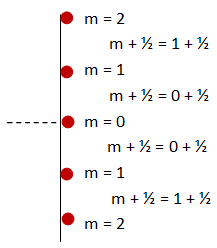
The second are related role that m plays is to track the number of wavelengths different between the two paths. In other words, remember that the rays come from a single wave incident on the double slit barrier. The two rays start out in phase. If one of the rays travels some whole number of wavelengths further than the other (if m = 1, 2, 3, etc.), the waves are once again in phase. Waves of the same phase add constructively--they give a bright spot. If the path differenceis a whole number of wavelengths plus an additional half wavelength longer, the waves will be out of phase and add desctructively. They will cancel out. At the center of the pattern, the waves travel the same distance. m = 0. Each additional spot out is an increase in path difference by a wavelength.
Remember that the rays come from a single wave incident on the double slit barrier. In other words, the two rays start out in phase. If one of the rays travels a whole number of wavelengths plus an additional half wavelength further than the other, the waves will be out of phase and add desctructively. They will cancel out. This is because a whole number of wavelengths maintains the same phase relationship but an additional half wavelength is 1800 out of phase
λ is the symbol for wavelength of the wave.
d is the symbol for the separation or distance between the two openings.
θ is the angle between the line of sight to the spot of interest as measured against a line straight down the center of the experiment.

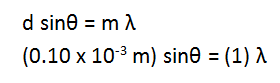
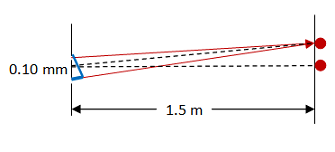
At this point, you will recognize that you have one equation but two unknowns. You want to solve for wavelength so that you can learn color, so there must be other information in the problem that can help you find θ. You can see the triangle you need in the simplified drawing below.
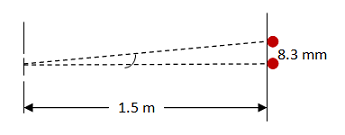
From this drawing, you can see that tanθ = (8.3 x 10-3m)/(1.5 m) = 0.0055. θ = 0.3170.
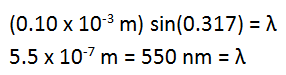
You can look up this wavelength of light in your text book or on line to find that the laser must be green.
How did you know to use the triangle to find θ?
In part from experience with problems like this, and in part because starting with the key physics interaction sets you up confidently in your process. So if you have worked similar problems, you probably recognized from the beginning that distances would need to be converted into an angle. But if this type of problem is new to you, you did not need to realize the side step of the problem until I mention it above. If you tried to look for an equation relating wavelength and distances, you would have been very frustrated. But if you were confident that your equation choice was based on the relevant physics, discovering an extra unknown is just an indication that there is additional, related, information in the problem.
How did you know m = 1?
In this case, you are told the separation between adjacent dots, so you can find θ between any two dots. You know that the m=0 dot is straight down the center (θ = 0) and so the easiest choice is to look at the m=1 dot which would be 8.3 mm up from the center.
Remember that in this formula, d represents the distance between the openings and not the distance to the screens or between the dots.
m numbers the dots in the pattern. In this case, you are told the separation between adjacent dots, so you can find θ between any two dots. You know that the m=0 dot is straight down the center (θ = 0) and so the easiest choice is to look at the m=1 dot which would be 8.3 mm up from the center.
Make sure that you know what the symbols in your equations represent. In this case, the "m" represents the unit of meters and not the dot number.
tanθ = (opposite side)/(adjacent side).
Wavelengths of light are frequently tabulated in nanometers. 1 nm = 10-9 meter.
As always, do not keep more significant figures in your answer than were given in the problem.

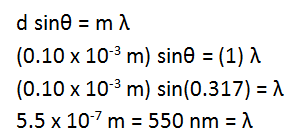
The bright and dark spots you see on the wall after the laser goes through a double slit grating result from the interference of the two beams created by the openings. This is therefore a standing wave pattern. The double slit interference equation includes all of the geometry showing where waves are in or out of phase. As long as you understand the symbols in the equation and how each side related to path length, you can work the problem in a straightforward fashion. In this case, the distances provided allowed you to find θ, and once you found wavelength you could determine color.
The statement of the problem implied that the answer should be in the visible range of light, and, indeed, you found that a laser that produces this pattern must be green light. If you have seen this set up in lab or lecture, you also know that the fringes (colored bands) are very close together as the problem suggests.
This problem asks about color. How do I find an equation?
As always, don't focus on what is given or requested. Focus on the key physics of the problem. In other words, begin by identifying the type of problem and you will quickly see that the location of the dots depends on the wavelength (and therefore color) of the light.
What is a double slit apparatus?
A double slit apparatus is an opaque screen that blocks the light except for two very thin openings or slits.
