You want to paddle a boat straight across the Mississippi River. You are able to paddle the boat with a speed of 5.6 mph relative to the water, and the current flows at a speed of 1.2 mph. What direction, relative to the river bank, do you need to point the boat? How fast do you move relative to land?
-
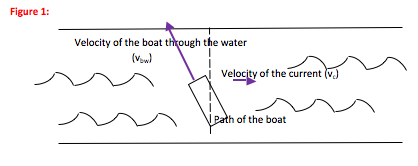
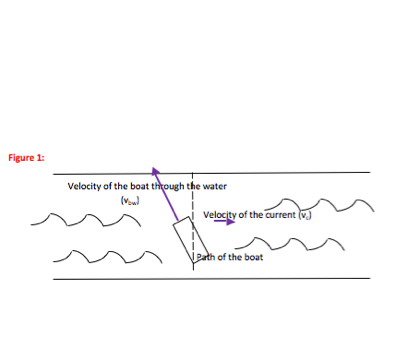
The actual motion of the boat (relative to land) is equal to the velocity of the boat through the water plus the velocity of the water. (Think about carrying a bowl of water while a fish swims in that bowl.) Written in symbols,
boat relative to land = vboat relative to water + vcurrent
Therefore, this is a velocity addition problem. In other words, it is a math problem asking you to practice working with vector components.
If you thought of this as a vector component problem because you recognized that you are given one side and the hypotenuse of a triangle and asked for the other side and one angle, that is also great and will give you the same approach to the solution. -
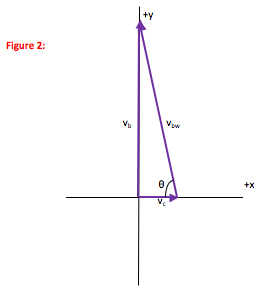
Remember, vectors are added head to tail. In other words, to show the addition of A + B, draw vector A and then draw the starting point (tail) of B at the ending point (head) of A. The sum is the vector that goes from the tail of A to the head of B.
In this case, you are told that the velocity relative to land is straight across the river, and so you need to draw the direction of vbw such that the sum is straight across (I chose this as the +y direction.)
-

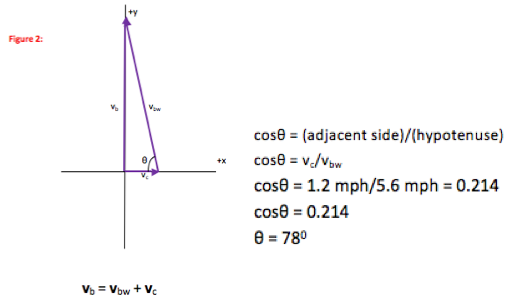
In this case, the three vectors form the sides and hypotenuse of a right triangle. So we do not need to divide vectors into components, we can just look at the four relations for a right triangle:
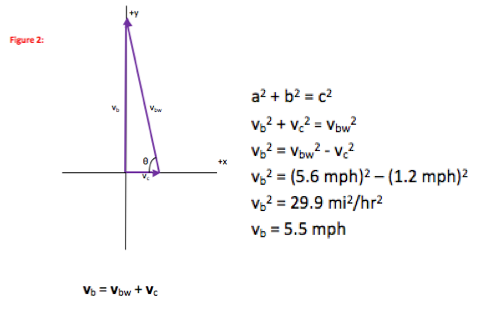
- a2 + b2 = c2
- Sinθ = (opposite side)/(hypotenuse)
- Cosθ = (adjacent side)/(hypotenuse)
- Tanθ = (opposite side)/(adjacent side)
The last three relations are often remembered as soh-cah-toa. In this case, you know the the hypotenuse (vbw) and one side (vc) and want to find the other side and one angle.
Relation 1. will give the third side if you know two, and equation 3. relates the given adjacent side and hypotenuse to the unknown angle.
-
Step 1
You need to point your boat at an angle of 780 from the bank of the river as shown in the picture (120 from straight across, into the current) in order to go straight across the river. Scroll down to find the speed of the boat relative to land.
-----------------------------------------------------------------------------------------
Step 2
The boat moves at a speed of 5.5 mph relative to the ground if you row it at a speed of 5.6 mph directed 780 from the bank in this current.
As shown in the equation and discussed in the identification of the problem, the actual motion of the boat relative to land (vb) depends both on how you row the boat (vbw) and on the current that carries the water downstream (vc). If you want a path that is straight across the river as specified in this problem, you need to point the boat at an angle into the current so that it is not carried downstream
The speed at which you row a boat is the speed at which it moves through the water, not the resulting speed relative to land. (If a fish can swim through the water in the bowl at a certain speed, its motion relative to the floor is that velocity plus any motion of the bowl.) Therefore, it is vbw and not vb that is 5.6 m/s.
The current in a river is the motion of water along the direction of the river. In other words, it is the flow of the water in the river.
It is equally fine to use any of the last three equations to find the direction you need to point the boat. If you use equation 2 or 4, you will need to find the speed of the boat relative to the ground (vb, the opposite side) before you can find the angle.
To find the angle, use “inv cos” or “cos-1” of 0.214 on your calculator.
Even though the speed of the boat relative to land (vb) is the unknown quantity, it is not the hypotenuse. This is clear if you work from the drawing rather than focusing on which value is the unknown. If the drawing isn’t clear, click here to return to the Identify the Problem page for a discussion of the relationship between velocities.
For the angle I chose in the figure, the current is the adjacent side—it touches the angle. If you work with the other angle in the triangle, velocity of current is the opposite side and so you should use sine of that angle.
Remember that you are subtracting (1.2 mph)2 from (5.6 mph)2. In other words, don’t square the – sign. You need to row faster than the boat actually travels, because some of your effort goes to countering the current.
How did you know the direction of the current?
The current in a river is the motion of water along the direction of the river. In other words, it is the flow of the water in the river.
How did you know that Vb and not Vbw is in the y-direction?
As shown in the equation and discussed in the identification of the problem, the actual motion of the boat relative to land (vb) depends both on how you row the boat (vbw) and on the current that carries the water downstream (vc). If you want a path that is straight across the river as specified in this problem, you need to point the boat at an angle into the current so that it is not carried downstream
Can’t I use equation 2 or 4 to get the angle?
It is equally fine to use any of the last three equations to find the direction you need to point the boat. If you use equation 2 or 4, you will need to find the speed of the boat relative to the ground (vb, the opposite side) before you can find the angle.
Isn’t vb the hypotenuse, not vbw?
Even though the speed of the boat relative to land (vb) is the unknown quantity, it is not the hypotenuse. This is clear if you work from the drawing rather than focusing on which value is the unknown. If the drawing isn’t clear, click here to return to the Identify the Problem page for a discussion of the relationship between velocities.
-

cosθ = vc/vbw, θ = 78o
vb2 + vc2 = vbw2, vb = 5.5 mph
This problem asked you only to practice the math of working with vector components. A good double check is that no component is greater than the length of the vector, and that the shorter component is less than the longer one. It is also a good idea to go back to the picture to make sure that all of your values and directions make sense.
In this case, you were not given two vectors to add, but rather were given the sum and one component vector. It is much easier to work this problem correctly using a picture rather than focusing on the unknown quantities.
In this case, you expect that the speed of the boat relative to land should be less than the speed at which you row it, because part of your efforts go to countering the current. In addition, the current is only a little over a fifth as strong as your rowing speed, and so you expect that your deviation from “straight across” (900) won’t be very large.
- No FAQs
