You drive a car due north at a speed of 64 km/hr for 21 km, and then you accelerate to 96 km/hr and continue north for another 45 minutes. What is your average velocity?
-
In this problem, you are given information about the velocity, displacement, and time of a car over different legs of a trip, and asked for the average velocity. v, x, and t are all related through the definition of velocity, and so this is a definition problem.
In general, if you are told about the rate at which some variable changes (in this case, x) you should check to see if you can work the problem just through the relevant definition.
-
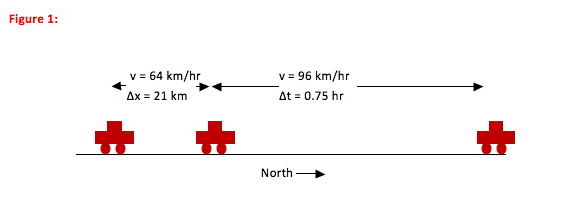
There is no need for a picture in most definition problems. In this case, however, a picture may help you visualize the motion and understand the importance of using the definition equation to find your average velocity. It is not, however, required if you are comfortable with velocity. You are given distance, time and velocity information over two legs of a trip and asked for the average velocity of the entire trip. A picture will not provide any additional organization beyond what is already present in the problem.
-
In equation form, the definition of average velocity is given by
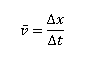
This is the only relation you need for this problem.
-
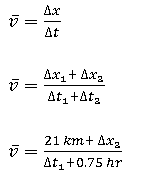
At this point, you need to use the rest of the information given in the problem to find the distance covered in the second leg of the trip and the time required for the first leg of the trip:

You can now return to the average velocity equation for the entire trip:

The average velocity of the car is 86km/hr north. No further solution is needed.
In this problem, speeds were given in units of km/hr. I know that I need to use the same unit system throughout the problem, and so I will either need to convert all speeds to km/min or convert all times to hrs. I chose to convert time to hours (45 min/(60 min/hr) = 0.75 hr) so that my final answer will be in km/hr.
Because the car continually moves north, this is a one-dimensional problem. You do not need to divide velocity or displacement vectors into components, and the displacement (Δx) is equal to the distance covered.
The total displacement of the car (xfinal - xinitial) is the distance covered in leg one plus the distance covered in leg two. The total time it takes is the time spent at 64 km/hr + the time spent at 96 km/hr.
In this problem, speeds were given in units of km/hr. I know that I need to use the same unit system throughout the problem, and so I will either need to convert all speeds to km/min or convert all times to hrs. I chose to convert time to hours (45 min/(60 min/hr) = 0.75 hr) so that my final answer will be in km/hr.
64 km/hr = 21 km/Δt1
(64 km/hr) Δt1 = 21 km
Δt1 = 21 km/(64 km/hr) = (21/64)(km/km/hr)
Δt1 = 0.33 (km x hr/km) = 0.33 hr
Can’t I just take (64 km/hr + 96 km/hr)/2 to find the average?
No. The car does not spend the same amount of time at each speed, and so the speeds do not contribute equally to the average. Think of it this way: Suppose you want to average 60 mph on a trip to visit a friend who lives 60 miles away. If you are behind a slow car and travel at a speed of 30 mph for the first 30 miles (taking one hour to do so) you would then have to travel at an infinite speed for the last 30 miles in order to cover the full 60 miles in one hour. If you traveled at 90 mph as the equation above suggests [60 mph = (30 mph + 90 mph)/2] for the last 30 miles it would take 1/3 hour more to complete the trip, so you would have averaged a speed of 60 m/1.33 hr = 45 mph not 60 mph. Always use v = Δx/Δt to find average velocity!
It seems like you use speed and velocity interchangeably in your solution. Aren’t they different?
They are different but related. In addition to being distance divided by time, speed is used to mean the magnitude of velocity at any given point. For example in this problem, the velocity of the car in leg one is 64 km/hr north, and the speed is 64 km/hr. It is equally correct to use “magnitude of velocity” in place of “speed” in this discussion.Can’t I just take (64 km/hr + 96 km/hr)/2 to find the average?
No. The car does not spend the same amount of time at each speed, and so the speeds do not contribute equally to the average. Think of it this way: Suppose you want to average 60 mph on a trip to visit a friend who lives 60 miles away. If you are behind a slow car and travel at a speed of 30 mph for the first 30 miles (taking one hour to do so) you would then have to travel at an infinite speed for the last 30 miles in order to cover the full 60 miles in one hour. If you traveled at 90 mph as the equation above suggests [60 mph = (30 mph + 90 mph)/2] for the last 30 miles it would take 1/3 hour more to complete the trip, so you would have averaged a speed of 60 m/1.33 hr = 45 mph not 60 mph. Always use v = Δx/Δt to find average velocity!
It seems like you use speed and velocity interchangeably in your solution. Aren’t they different?
They are different but related. In addition to being distance divided by time, speed is used to mean the magnitude of velocity at any given point. For example in this problem, the velocity of the car in leg one is 64 km/hr north, and the speed is 64 km/hr. It is equally correct to use “magnitude of velocity” in place of “speed” in this discussion.
Can’t I just take (64 km/hr + 96 km/hr)/2 to find the average?
No. The car does not spend the same amount of time at each speed, and so the speeds do not contribute equally to the average. Think of it this way: Suppose you want to average 60 mph on a trip to visit a friend who lives 60 miles away. If you are behind a slow car and travel at a speed of 30 mph for the first 30 miles (taking one hour to do so) you would then have to travel at an infinite speed for the last 30 miles in order to cover the full 60 miles in one hour. If you traveled at 90 mph as the equation above suggests [60 mph = (30 mph + 90 mph)/2] for the last 30 miles it would take 1/3 hour more to complete the trip, so you would have averaged a speed of 60 m/1.33 hr = 45 mph not 60 mph. Always use v = Δx/Δt to find average velocity!
It seems like you use speed and velocity interchangeably in your solution. Aren’t they different?
They are different but related. In addition to being distance divided by time, speed is used to mean the magnitude of velocity at any given point. For example in this problem, the velocity of the car in leg one is 64 km/hr north, and the speed is 64 km/hr. It is equally correct to use “magnitude of velocity” in place of “speed” in this discussion.
Do I have to use the definition of velocity for this question? Can’t I just add the velocities together and divide by two?
See Q&A's Below
Can’t I just take (64 km/hr + 96 km/hr)/2 to find the average?
No. The car does not spend the same amount of time at each speed, and so the speeds do not contribute equally to the average. Think of it this way: Suppose you want to average 60 mph on a trip to visit a friend who lives 60 miles away. If you are behind a slow car and travel at a speed of 30 mph for the first 30 miles (taking one hour to do so) you would then have to travel at an infinite speed for the last 30 miles in order to cover the full 60 miles in one hour. If you traveled at 90 mph as the equation above suggests [60 mph = (30 mph + 90 mph)/2] for the last 30 miles it would take 1/3 hour more to complete the trip, so you would have averaged a speed of 60 m/1.33 hr = 45 mph not 60 mph. Always use v = Δx/Δt to find average velocity!
It seems like you use speed and velocity interchangeably in your solution. Aren’t they different?
They are different but related. In addition to being distance divided by time, speed is used to mean the magnitude of velocity at any given point. For example in this problem, the velocity of the car in leg one is 64 km/hr north, and the speed is 64 km/hr. It is equally correct to use “magnitude of velocity” in place of “speed” in this discussion.
Why did you change the units on time when you made the drawing?
In this problem, speeds were given in units of km/hr. I know that I need to use the same unit system throughout the problem, and so I will either need to convert all speeds to km/min or convert all times to hrs. I chose to convert time to hours (45 min/(60 min/hr) = 0.75 hr) so that my final answer will be in km/hr.
1. Do I have to use the definition of velocity for this question? Can’t I just add the speeds together and divide by two?
See Q&A's Below
Can’t I just take (64 km/hr + 96 km/hr)/2 to find the average?
No. The car does not spend the same amount of time at each speed, and so the speeds do not contribute equally to the average. Think of it this way: Suppose you want to average 60 mph on a trip to visit a friend who lives 60 miles away. If you are behind a slow car and travel at a speed of 30 mph for the first 30 miles (taking one hour to do so) you would then have to travel at an infinite speed for the last 30 miles in order to cover the full 60 miles in one hour. If you traveled at 90 mph as the equation above suggests [60 mph = (30 mph + 90 mph)/2] for the last 30 miles it would take 1/3 hour more to complete the trip, so you would have averaged a speed of 60 m/1.33 hr = 45 mph not 60 mph. Always use v = Δx/Δt to find average velocity!
It seems like you use speed and velocity interchangeably in your solution. Aren’t they different?
They are different but related. In addition to being distance divided by time, speed is used to mean the magnitude of velocity at any given point. For example in this problem, the velocity of the car in leg one is 64 km/hr north, and the speed is 64 km/hr. It is equally correct to use “magnitude of velocity” in place of “speed” in this discussion.
How did you solve for Δt1?
64 km/hr = 21 km/Δt1
(64 km/hr) Δt1 = 21 km
Δt1 = 21 km/(64 km/hr) = (21/64)(km/km/hr)
Δt1 = 0.33 (km x hr/km) = 0.33 hr
Do I have to use the definition of velocity for this question? Can’t I just add the speeds together and divide by two?
See Q&A's Below
Can’t I just take (64 km/hr + 96 km/hr)/2 to find the average?
No. The car does not spend the same amount of time at each speed, and so the speeds do not contribute equally to the average. Think of it this way: Suppose you want to average 60 mph on a trip to visit a friend who lives 60 miles away. If you are behind a slow car and travel at a speed of 30 mph for the first 30 miles (taking one hour to do so) you would then have to travel at an infinite speed for the last 30 miles in order to cover the full 60 miles in one hour. If you traveled at 90 mph as the equation above suggests [60 mph = (30 mph + 90 mph)/2] for the last 30 miles it would take 1/3 hour more to complete the trip, so you would have averaged a speed of 60 m/1.33 hr = 45 mph not 60 mph. Always use v = Δx/Δt to find average velocity!
It seems like you use speed and velocity interchangeably in your solution. Aren’t they different?
They are different but related. In addition to being distance divided by time, speed is used to mean the magnitude of velocity at any given point. For example in this problem, the velocity of the car in leg one is 64 km/hr north, and the speed is 64 km/hr. It is equally correct to use “magnitude of velocity” in place of “speed” in this discussion.
-
Average velocity is one of the most frequently missed types of definition problem. Unless the object spends the same amount of time at each speed, you cannot just add the speeds and divide by two. Instead, you have to use the definition of average velocity, and divide the total distance covered by the car by the total amount of time required.

Because the car spent more time traveling at 96 km/hr than it did traveling at 64 km/hr, it makes sense that the average speed is closer to 96 than to 64. Average velocity is the average speed and the direction, or 86 km/hr north.
