You throw a 0.14 kg baseball 2.7 m into the air. How much does its gravitational potential energy change as it goes up?
-
In this problem, you are given the change in height of a baseball and asked for the change in its gravitational potential energy. Potential energy is defined as the energy of position as related to a conservative force (such as gravity), so you aren’t asked for new information in this problem but rather to restate what you know about motion in a slightly different way.
-
There is no need for a picture in most definition problems, and this is one of them. You are given height information asked for the closely-related gravitational potential energy. A picture will not provide any additional insight or organization beyond what is already present in the problem.
-
In equation form, gravitational potential energy is defined as
PEg = mgh
This is the only relation you need for this problem. -
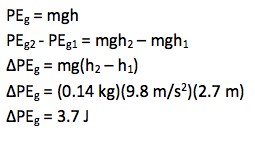
There is no further calculation required in this problem.
Some books use U as a symbol for potential energy, and others use PE or P.E. These are all equivalent and refer to the same thing.
The MKS unit of force is the Joule. 1 J = 1 kg m2/s2.
In this problem, mass was given in kg, g is in m/s2 and height was given in m
Only two significant figures were provided in this problem, so only two figures were kept in the solution.
How do you know the units for KE are Joules?
The MKS unit of force is the Joule. 1 J = 1 kg m2/s2.
In this problem, mass was given in kg, g is in m/s2 and height was given in m
Where is the h=0 point?
It doesn’t matter. Whether you call the ground or your hand or any other point h=0, Δh (the change in the height of the ball) is always 2.7 m.
Why do you call this a definition problem rather than an energy problem?
Conservation of energy allows you to compare two (or more) different points in a motion and learn something about energy changes in that motion through the comparison. So this looks on the surface like an energy problem. However, you don’t have (or want) any information about the other forms of energy involved, such as the change in kinetic energy of the ball. Further, there is a very distinct pairing between height and gravitational potential energy. So to find PEg from h or vice versa is merely a way of restating information that you already have.
Where is the h=0 point in this problem?
It doesn’t matter. Whether you call the ground or your hand or any other point h=0, Δh (the change in the height of the ball) is always 2.7 m.
Why do you call this a definition problem rather than an energy problem?
Conservation of energy allows you to compare two (or more) different points in a motion and learn something about energy changes in that motion through the comparison. So this looks on the surface like an energy problem. However, you don’t have (or want) any information about the other forms of energy involved, such as the change in kinetic energy of the ball. Further, there is a very distinct pairing between height and gravitational potential energy. So to find PEg from h or vice versa is merely a way of restating information that you already have.
Where is the h=0 point in this problem?
It doesn’t matter. Whether you call the ground or your hand or any other point h=0, Δh (the change in the height of the ball) is always 2.7 m.
Why do you call this a definition problem rather than an energy problem?
Conservation of energy allows you to compare two (or more) different points in a motion and learn something about energy changes in that motion through the comparison. So this looks on the surface like an energy problem. However, you don’t have (or want) any information about the other forms of energy involved, such as the change in kinetic energy of the ball. Further, there is a very distinct pairing between height and gravitational potential energy. So to find PEg from h or vice versa is merely a way of restating information that you already have.
Where is the h=0 point in this problem?
It doesn’t matter. Whether you call the ground or your hand or any other point h=0, Δh (the change in the height of the ball) is always 2.7 m.
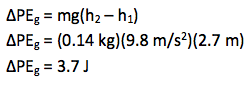
This problem is merely a definition problem. You will use the definition of potential energy in Conservation of Energy problems, much as you use Fg = mg when you solve force problems. Whenever you have information about the height of an object, you can restate that information as its gravitational potential energy (or vice versa.)
The MKS unit of energy is the Joule. For context, one Joule is the amount of energy required to lift a one N (0.22 lb) object one meter (3.3 ft) in the air. In this case, the weight (mg) of the baseball is (0.14 kg)(9.8 m/s2) or 1.4 N and so your answer makes sense.
