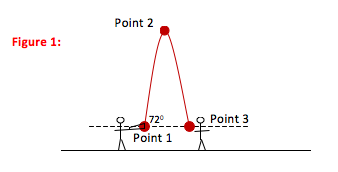
A major league baseball player hits a fly ball. The ball leaves the bat with a velocity of 41 m/s at an angle of 72o above the horizontal. How far from home plate does the center fielder need to stand if he is going to catch the ball at the same height from which it was hit?
-
In this problem, you are asked to describe the motion (how far it travels before it returns to its original height) of a baseball. Whenever you are asked to describe the motion of an object without worrying about the cause of that motion, you have a kinematics problem.
-
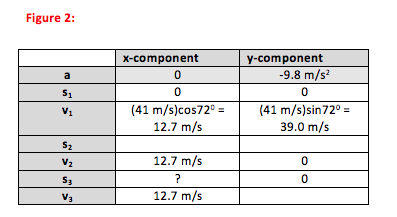
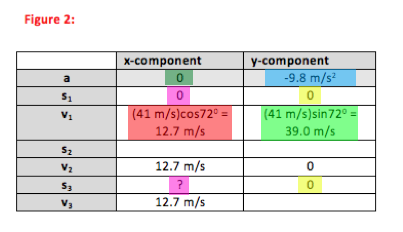
There are three key kinematic equations. If you carefully select the equation which most directly describes the situation in your problem, you will not only solve the problem in fewer steps but also understand it better. The three equations, written for motion in the y-direction, are:
1. y = y0 + v0yΔt + ½ ay(Δt)2 (relates position and time)
2. vy = v0y + ayΔt (relates velocity and time)
3. vy2 = v0y2 + 2ay(Δy) (relates velocity and position)
In this problem, you are asked where to stand to catch the ball (x-position of the ball) when it returns to its original height (y-position) of the ball. But position is a vector—you cannot mix x- and y-components in the same equation.
Whenever you are asked about the x-direction and told about the y-direction, or vice versa, you need to use time to go between the two.
The amount of time that the baseball spends going from the original height to the final height is the same as the amount of time it takes to go from the bat to the center fielder. So you can use what you know about the y-position of the ball to find the time it spends in the air (equation 1 in the y-direction) and then use that time to find its x-position (equation 1 in the x-direction.)
-
Step 1:
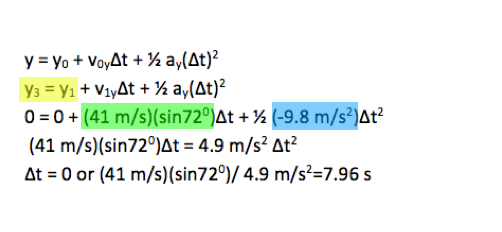
Equation 1 will always give two solutions for time. In this case, t = 0 corresponds to the time that the ball left the bat, and t = 7.96 s corresponds to the time that it returned to that same height in center field. Now that you know how long the ball was in the air, proceed to step 2 to find how far it traveled.
--------------------------------------------------------------------------------------------
Step 2:
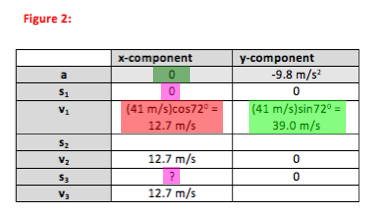

The problem asked how far the base ball traveled from home plate. No further mathematical solution is necessary.
Unless a problem states otherwise, you can assume that air resistance on a small object thrown as a projectile is negligible. Therefore, the only significant cause of the ball’s acceleration is gravity. For all objects near the Earth’s surface, the downward acceleration due to gravity, g, has a value of 9.8 m/s2. (If you have already studied forces, you can see this quickly with a free body diagram.) So the x-component of the ball’s acceleration is 0, and the y-component is -9.8 m/s2. These values are true throughout the problem and not just at any one point.
The first point described in the problem is when the ball leaves the bat. I chose that point to be x = 0 and y = 0. I can pick the origin of the coordinate system anywhere that is convenient, and all other locations are then referenced from that choice. With this choice, other horizontal distances in the problem will be relative to home plate, and other vertical distances relative to where the ball left the bat.
Because the initial velocity is at an angle to the axes, you need to divide it into its x- and y-components.
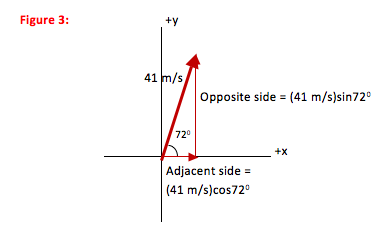
As you can see in the figure, the x- and y-components of a vector make up the sides of a right triangle. The vector itself forms the hypotenuse (h). The side of the triangle opposite the angle that you use is given by h sinθ and the side that touches the angle you use is given by h cosθ (soh cah toa).
In this case, the x-component is adjacent to the 72o angle, and so can be given by (41 m/s)cos72o as shown. Likewise, the y-component is opposite to the 72oangle and is therefore given by (41 m/s)sin72o.
720 above the horizontal means that if you start with a horizontal line (in the +x direction) and rotate it counter-clockwise by 720 you will have the correct path for the ball.
The first point described in the problem is when the ball leaves the bat. I chose that point to be x = 0 and y = 0. I can pick the origin of the coordinate system anywhere that is convenient, and all other locations are then referenced from that choice. Therefore, other horizontal distances in the problem will be relative to home plate, and other vertical distances relative to where the ball left the bat.
Because the initial velocity is at an angle to the axes, you need to divide it into its x- and y-components.
You are not given information about this point in the motion, nor are you asked about it. Therefore, you do not need to include Point 2 in the table. If you do ever need information about the top of the motion, remember that the y-component of velocity is zero at the top of the arc. There is no acceleration in the x-direction and so the x-component of the ball’s velocity does not change.
We know that the ball was caught at the same height at which it was hit, and so y3=y1=0. Because x=0 was chosen to be home plate, when we solve our equations for x3 we will know the distance from home plate.
We do not know the velocity in the y-direction (although you may recognize that in the absence of air resistance it has the same magnitude as it had going up at the same height) and in the x-direction it remains constant because ax=0.The kinematic variables (s, v, a) are vectors, and therefore you will work with kinematic equations in one dimension (x- or y-) at a time. Therefore, you will work only with x- or y-components of these variables.
The t in the kinematic equations refers to the time interval between the two points in the equation, with y0 occurring at the earlier time. I use Δt rather than t to be explicit that this is a time interval (t – t0) and not a point in time.
Some text books will give more than three kinematic equations—for example, they may provide “range equations” or different versions of the equations for horizontal and vertical motion. Those are just these three equations solved for special cases. In my view, it is better to know and understand three equations that will always work than to memorize many equations which are specific to certain situations only.You need to find how long it takes the ball to go from home plate (Point 1) to center field (Point 3). Therefore, “y0” and “y” are “y1” and “y3” respectively.
The acceleration of the ball (due to gravity) is downward, which is the negative y-direction as chosen in this problem. Because a, v, and y are all vector quantities, their values are given a + or – sign to represent direction whenever they are filled into any of the kinematic equations.
It is perfectly fine to fill 39 m/s in for v1y, and in fact involves less calculation since you already simplified (41 m/s)(sin720) when you made the table. I used the pre-simplified expression of “(41 m/s)(sin720)” merely to emphasize once again that you only want to include the y-component of v1 in this equation.
The expression 0 = 0 + (41 m/s)(sin720)Δt + ½ (-9.8 m/s2)Δt2 can be factored and written as 0 =(41 m/s sin720 – 4.9 m/s2Δt)Δt. In other words, I pulled a Δt out from each term. You now have an expression of the form 0 = Ax B, so either A (41 m/s sin720 – 4.9 m/s2Δt) = 0 or B (Δt) = 0.
You are asked to find how far the ball travels from home plate (Point 1) to center field (Point 3). Therefore, “x0” and “x” are “x1” and “x3” respectively.
The acceleration of the baseball in the y-direction is - 9.8 m/s2. However, there are no forces acting on the baseball in the x-direction, and so ax = 0.
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
It is perfectly fine to fill 12.7 m/s in for v1x, and in fact involves less calculation since you already simplified (41 m/s)(cos720) when you made the table. I used the pre-simplified expression of “(41 m/s)(cos720)” merely to emphasize once again that you only want to include the x-component of v1 in this equation.
What is the acceleration of the ball? How do you know?
Unless a problem states or implies otherwise, you can assume that air resistance on a small object thrown as a projectile is negligible. Therefore, the only significant cause of the ball’s acceleration is gravity. For all objects near the Earth’s surface, the downward acceleration due to gravity, g, has a value of 9.8 m/s2. (If you have already studied forces, you can see this quickly with a free body diagram.) So the x-component of the ball’s acceleration is 0, and the y-component is -9.8 m/s2.
How do you pick x and y = 0?
All that matters for describing motion is that you explicitly state where your reference point is. In this case, the ball was caught at its original height and so I chose that, rather than the ground, to be y = 0. Therefore, any heights that I find in the problem will be heights above the point at which the ball was hit. I chose x = 0 to be the starting point of the problem—home plate—so any distances that I find will be relative to home plate.
What is s?
s is the vector symbol for displacement—in other words, the vector whose components are x- and y-. Some books use x and others use r instead of s, so use whichever variable is comfortable for you.
Do I have to fill in the table?
Using a table like this in two dimensional kinematic problems can reduce one of the most common errors that students make on exams. The kinematic variables are vectors, and so you can only work in one dimension at a time. So you need to divide vectors into components. However, you also have three equations in each direction and so you need to think about which equation to use. It is very common for students to go to the work of finding the components for the vectors, but then to use the full vector (in this case, 41 m/s) rather than the appropriate component when it is time to solve the equation, or to use -9.8 m/s2 for acceleration in the x-direction as well is the y-direction . By organizing your information into a table and working with only the x- or y- column at a time, you are less likely to make these mistakes when you solve the problem.
How do you know acceleration?
Unless a problem states or implies otherwise, you can assume that air resistance on a small object thrown as a projectile is negligible. Therefore, the only significant cause of the ball’s acceleration is gravity. For all objects near the Earth’s surface, the downward acceleration due to gravity, g, has a value of 9.8 m/s2. (If you have already studied forces, you can see this quickly with a free body diagram.) So the x-component of the ball’s acceleration is 0, and the y-component is -9.8 m/s2.
How do you find the components of velocity?
Because the initial velocity is at an angle to the axes, you need to divide it into its x- and y-components.

As you can see in the figure, the x- and y-components of a vector make up the sides of a right triangle. The vector itself forms the hypotenuse (h). The side of the triangle opposite the angle that you use is given by h sinθ and the side that touches the angle you use is given by h cosθ (soh cah toa).
In this case, the x-component is adjacent to the 72o angle, and so can be given by (41 m/s)cos72o as shown. Likewise, the y-component is opposite to the 72oangle and is therefore given by (41 m/s)sin72o.
Why do I have to divide the vectors into components?
The kinematic variables (s, v, a) are vectors, and therefore you will work with kinematic equations in one dimension (x- or y-) at a time. Therefore, you will work only with x- or y-components of these variables.
My book uses “t” rather than “Δt” in the equations. Is that ok?
or
My book gives more than three equations. Why do you only use these three?
The t in the kinematic equations refers to the time interval between the two points in the equation, with y0 occurring at the earlier time. I use Δt rather than t to be explicit that this is a time interval (t – t0) and not a point in time.
Some text books will give more than three kinematic equations—for example, they may provide “range equations” or different versions of the equations for horizontal and vertical motion. Those are just these three equations solved for special cases. In my view, it is better to know and understand three equations that will always work than to memorize many equations which are specific to certain situations only.How did you know which two points to pick?
You need to find how long it takes the ball to go from home plate (Point 1) to center field (Point 3). Therefore, “y0” and “y” are “y1” and “y3” respectively.
Why is 9.8 m/s2 negative?
The acceleration of the ball (due to gravity) is downward, which is the negative y-direction as chosen in this problem. Because a, v, and y are all vector quantities, their values are given a + or – sign to represent direction whenever they are filled into any of the kinematic equations.
Why didn’t you use 39.0 m/s for v1y?
It is perfectly fine to fill 39 m/s in for v1y, and in fact involves less calculation since you already simplified (41 m/s)(sin720) when you made the table. I used the pre-simplified expression of “(41 m/s)(sin720)” merely to emphasize once again that you only want to include the y-component of v1 in this equation.
How did you know which two points to pick?
You are asked to find how far the ball travels from home plate (Point 1) to center field (Point 3). Therefore, “x0” and “x” are “x1” and “x3” respectively.
Why is acceleration 0? Isn’t it - 9.8 m/s2?
The acceleration of the baseball in the y-direction is - 9.8 m/s2. However, there are no forces acting on the baseball in the x-direction, and so ax = 0.
My numbers are close but not exactly what is shown in the equation. Am I close enough?
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
How do you pick s = 0?
All that matters for describing motion is that you explicitly state where your reference point is. In this case, the ball was caught at its original height and so I chose that, rather than the ground, to be y = 0. Therefore, any heights that I find in the problem will be heights above the point at which the ball was hit. I chose x = 0 to be the starting point of the problem—home plate—so any distances that I find will be relative to home plate.
What is “s”?
s is the vector symbol for displacement—in other words, the vector whose components are x- and y-. Some books use x and others use r instead of s, so use whichever variable is comfortable for you.
Do I have to fill in the table?
Using a table like this in two dimensional kinematic problems can reduce one of the most common errors that students make on exams. The kinematic variables are vectors, and so you can only work in one dimension at a time. So you need to divide vectors into components. However, you also have three equations in each direction and so you need to think about which equation to use. It is very common for students to go to the work of finding the components for the vectors, but then to use the full vector (in this case, 41 m/s) rather than the appropriate component when it is time to solve the equation, or to use -9.8 m/s2 for acceleration in the x-direction as well is the y-direction . By organizing your information into a table and working with only the x- or y- column at a time, you are less likely to make these mistakes when you solve the problem.
My book uses variables like x, y0, v, v0, and t. Why do you use 1, 2 and 3 as subscripts, and Δt instead of t?
The kinematic equations relate position and velocity at any two points in the motion. Because many problems provide or ask about information at more than two points, I identify each point with its own subscript to keep them straight. I can then pick any two points to be s0 and s when I use the equations. The t in the kinematic equations refers to the time interval between the two points in the equation, with s0 occurring at the earlier time. I use Δt rather than t to be explicit that this is a time interval (t – t0) and not a point in time.
-


In this problem, you were asked to find how far a baseball travels during the time it spends going up and coming down to the same height. Displacement, velocity and acceleration are vector quantities, and so you cannot mix x- and y- components in the same equation. Therefore, you cannot use the y-position condition (same height) to solve for the x-position question (where to stand to catch the ball) in a single step.
You can always relate x- and y-motion through time—the ball spends as long going up and down as it spends going from home plate to center field. So we first solved for time required to go up and down (y-position) and then used that time to determine how far the ball traveled (x-position.)
