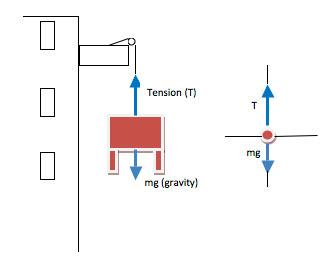
A moving company needs to lift a 700 lb. (320kg) piano to the top floor of an apartment building. They set up a rope and pulley system on the balcony of the upper story apartment, and pull the piano up. If the piano initially has an acceleration of 0.45 m/s2, what is the tension in the rope during that period of time?
-
In this problem, you are asked to relate motion (the acceleration of the piano) to force (tension). Force and motion of a single object are always related through Newton's Second Law, so this is a force or 2nd Law problem.
-
Tension is the result of the molecular attractions in the rope holding the rope together. Therefore, it always acts toward the center of a rope.
The free body diagram is a sketch of the forces on an object, or the causes of motion. Acceleration is the effect of those forces and therefore does not show up on the FBD. It will make an appearance in the equation.
All objects near Earth experience a downward force of gravity equal to mass of the object x 9.8 m/s2.
-
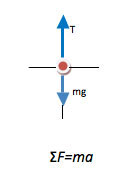
The key equation for any problem that relates forces and motion is Newton's Second Law. Regardless of what quantity you are asked to find, begin with the Second Law. If additional information is needed, it will become apparent as you proceed.
-
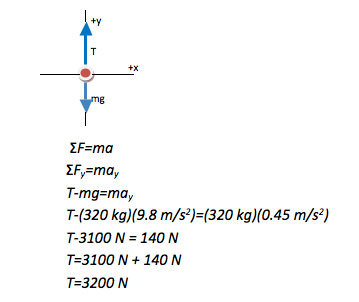
Tension is upward and therefore in the positive direction.
The force of gravity acts downward, which is the negative y-direction. Therefore, mg is given a negative sign in the equation. Do not also give 9.8 ms/s2 a negative sign, or you will double count the direction.
The acceleration of the piano is upward, which is the +y direction.
All forces on this object act vertically. Therefore, this is a one-dimensional problem and only needs to be solved in the y-direction.
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
No. It is true that you are given acceleration, which is one of the kinematic quantities. However, you do not have any information about the other descriptive kinematic variables such as velocity or position, and even if you did you would ultimately need to go through acceleration to get to force.
Can this problem be worked using kinematics?
No. It is true that you are given acceleration, which is one of the kinematic quantities. However, you do not have any information about the other descriptive kinematic variables such as velocity or position, and even if you did you would ultimately need to go through acceleration to get to force.
Why isn’t acceleration shown on the figure?
The free body diagram is a sketch of the forces on an object, or the causes of motion. Acceleration is the effect of those forces and therefore does not show up on the FBD. It will make an appearance in the equation.
Why did you choose down to be negative?
Can I pick the +y direction to be down?
Yes. In that case, mg would be in the +y direction, and a and T would be in the –y direction. Your answer will be the same in either case.
Why is 9.8 m/s2 positive?
The force of gravity acts downward, which is the negative y-direction. Therefore, mg is given a negative sign in the equation. Do not also give 9.8 ms/s2 a negative sign, or you will double count the direction.
My numbers are close but not exactly what is shown in the equation. Am I close enough?
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
Why isn’t normal force included on the free body diagram?
Normal force is the contact force between two surfaces. It pushes out from the surfaces and keeps them from falling into each other. In this case, the interaction between the piano and the rope is shown by tension. The piano is not resting on any surface.
Why isn’t there air resistance?
There is! However, air resistance depends on velocity (squared) as well as on cross sectional area, and so at low speeds (such as raising a piano on a rope) it is much smaller than the force of gravity on the piano and can therefore be ignored for the accuracy required in this problem.
Why isn’t buoyant force included on the free body diagram?
It is true that air puts a small buoyant force on the piano. However, the size of the upward buoyant force compared to the downward force of gravity is very small. (The ratio of the two is given by the ratio of the density of air to the density of a piano.) So to the number of significant figures included in this problem, we do not need to take buoyant force into account.
Why isn’t acceleration included on the free body diagram?
The free body diagram is a stylized drawing to help you visualize the cause of acceleration, and to directly map the drawing into the left hand side (ΣF) of Newton’s Second Law. Acceleration is the effect of the forces, and therefore is not included on the list of forces.
Can I pick the +y direction to be down?
Yes. In that case, mg would be in the +y direction, and a and T would be in the –y direction. Your answer will be the same in either case.
Why did you focus on the piano and not on the rope?
In this case, we don’t have much information about the rope. But we do know about the weight and motion of the piano. Because the motion of the piano depends on the tension in the rope, we can learn about the rope through the motion of the piano.
-

In this problem, the rope puts an upward force on the piano. The force by the rope needs to be strong enough to both support the piano against the force of gravity (3100 N) and to give it an upward acceleration. So tension needs to be greater than 3100 N.