A child on a sled has been given a push so that she is moving up a hill. The hill is covered with icy snow and can be treated as frictionless. The child has a mass of 22.7 kg; the sled has a mass of 3.18 kg. What is the acceleration of the child as she moves up the incline? How far will she go before coming to a stop if her speed is 2 m/s when she starts at the bottom of the hill? She holds on tightly and so does not fall off the sled, and the hill makes an angle of 15.5 0 with the horizontal.
-
In this problem, you are asked to relate motion (the sled moves up the hill) to force(even though forces are not explicitly stated, you know that the reason the child’s velocity changes is the gravitational force). Force and motion of a single object are always related through Newton’s Second Law, so this is a force or 2nd Law problem.
For the second part of the problem, you are asked to describe motion. The second question is a kinematics or energy problem.
Can this problem be worked using kinematics or energy?
No. In this case, you are explicitly asked for acceleration and don’t have any descriptive information about the child’s motion beyond her starting velocity.
-
Step 1
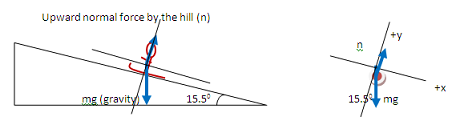
Your FBD is not yet finished, because mg has both x- and y- components. Continue down to step 2 when you are ready to continue.
Why isn't acceleration shown on the figure?
The free body diagram is a sketch of the forces on an object, or the causes of motion. Acceleration is the effect of those forces and therefore does not show up on the FBD. It will make an appearance in the equation.
Why did you pick the coordinate system to be along the angle of the incline?
You can select any coordinate system that you want to use. However, the math will always be easier if you pick one axis to be in the direction of acceleration. In this case, acceleration is along the incline.
How did you know where to put the 15.5oangle?
There are two ways to approach this question. If you think visually, exaggerate the small and large angles on your drawing. In other words, 15.5o is less than half of a right angle, so draw the slope of the incline to be very small. Then you can see that mg makes a smaller angle with the –y axis than it does with the +x axis, and the smaller angle is 15.5o.
If you think geometrically, use the fact that the two small angles on a right triangle add up to 90o. The triangle on the first drawing made by the ground, the incline, and mg is a right triangle, so the angle between the incline (the +x axis) and mg must be (90-15.5)o=74.5o. It is equally fine to use the 74.5o angle, just note that sin and cos are reversed (because which side is opposite and which is adjacent depends on the triangle you draw.) You will get the same answer because sin(74.5o)=cos(15.5o).
I chose to use the first method simply because that is an easier way to determine the correct angle for most students.
All objects near Earth experience a downward force of gravity equal to mass of the object x 9.8 m/s2. Because the child and the sled move together and so can be treated as a single system, m in this case refers to the total mass of the child plus the sled.
The initial motion of the child on the sled does not matter in the first part of the problem. Her acceleration is given by the forces that act on her, regardless of the direction or speed of her initial motion.
There are two ways to know where to put the 15.50 angle on your FBD. If you think visually, exaggerate the small and large angles on your drawing. In other words, 15.50 is less than half of a right angle, so draw the slope of the incline to be very small. Then you can see that mg makes a smaller angle with the –y axis than it does with the +x axis, and the smaller angle is 15.50.
If you think geometrically, use the fact that the two small angles on a right triangle add up to 900. The triangle on the first drawing made by the ground, the incline, and mg is a right triangle, so the angle between the incline (the +x axis) and mg must be (90-15.5)0. It is equally fine to use the 74.50 angle that mg makes with the +x axis.
This information tells you that the child and the sled move together. Because you don’t need to know anything about the forces between the child and the sled, you can treat them together as a single system.
Normal force is present whenever two objects are in contact with each other. Its direction is out from the objects and perpendicular to the surfaces. In this case, the incline pushes against the sled at an angle straight out from the surface of the incline.
-------------------------------------------------------------------------------------------
Step 2
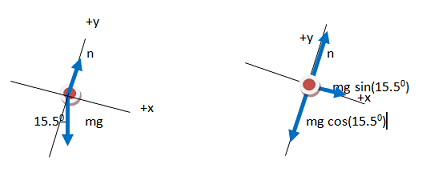
In the final FBD drawn here, all forces are divided into components. The contribution each force makes in the x-direction (along the incline) is shown explicitly, as is the contribution each force makes in the y-direction. The FBD is now a visual representation of ∑F=ma in each direction.
How did you divide gravity into its components?
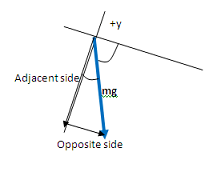
As you can see in the figure, the x- and y-components of a vector make up the sides of a right triangle. The vector itself forms the hypotenuse (h). The side of the triangle opposite the angle that you use is given by h sinθ and the side that touches the angle you use is given by h cosθ (soh cah toa)
In this case, the x-component is opposite to the 15.5o angle and adjacent to the 74.5oangle, and so can be given by mg sin(15.5o) as shown, or by mg cos(74.5o) if you chose to use that angle instead. Likewise, the y-component is adjacent to the 15.5oangle and is therefore given by mg cos(15.5o).
Isn't the x-component always cosθ and the y-component always sinθ?
No. Cosine goes with the component that is adjacent to θ, and sine goes with the component that is opposite to θ.
In this case, the x-component is opposite to the 15.5o angle and adjacent to the 74.5oangle, and so can be given by mg sin(15.5o) as shown, or by mg cos(74.5o) if you chose to use that angle instead. Likewise, the y-component is adjacent to the 15.5oangle and is therefore given by mg cos(15.5o).


As you can see in the figure, the x- and y-components of a vector make up the sides of a right triangle. The vector itself forms the hypotenuse (h). The side of the triangle opposite the angle that you use is given by h sinθ and the side that touches the angle you use is given by h cosθ (soh cah toa)
In this case, the x-component is opposite to the 15.5o angle and adjacent to the 74.5oangle, and so can be given by mg sin(15.5o) as shown, or by mg cos(74.5o) if you chose to use that angle instead. Likewise, the y-component is adjacent to the 15.5oangle and is therefore given by mg cos(15.5o).
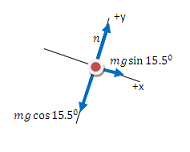
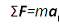
The key equation for any problem that relates forces and motion is Newton’s Second Law. Regardless of what quantity you are asked to find, begin with the Second Law. If additional information is needed, it will become apparent as you proceed.
At this stage in the problem , you do not need to think about the second question. Return to this page and click here when you are ready to select the relation for part b.
There are three key kinematic equations. If you carefully select the equation which most directly describes the situation in your problem, you will not only solve the problem in fewer steps but also understand it better. The three equations, written for motion in the x-direction, are:
1. x = x0 + v0Δt + ½ a(Δt)2 (relates position and time)
2. v = v0 + aΔt (relates velocity and time)
3. v2 = v02 + 2a(Δx) (relates velocity and position)
In this case, you are asked how far (position) the child on the sled travels in before coming to a stop (velocity), so you want to use equation 3.

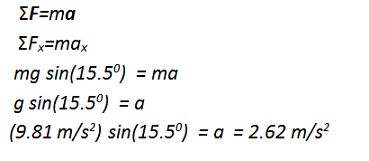
The problem asks for the acceleration of the sled. In this case, you know that the sled accelerates along the incline, or in the x-direction. You do not need to work in the y-direction to solve this problem.
Scroll down when you are ready to solve for the distance the sled covers.
Why is 9.81 m/s2 positive?
The force of gravity acts downward, which has a component in the -y direction and a component in the +x direction of this coordinate system . The correct sign is given in front of the force term in the equation. Do not also give 9.81 m/s2 a negative sign, or you will double count the direction. Note that 9.81 was used for g rather than 9.8, because three significant figures were given in the statement of the problem.
My numbers are close but not exactly what is shown in the equation. Am I close enough?
Only three significant figures were given in the text of the problem, so only three significant figures are included in the solution.
What happened to mass in the equation?
Because m is in both terms, it can be divided out.
Gravity acts both to pull the sled down along the incline (in the +x direction by this drawing) and to hold the sled into the incline (in the -y direction.) Only the portion of gravity acting in the direction or interest should be included in the x- or y- equation. In other words, the y-component of gravity has no effect on the acceleration of the sled along the hill.
The force of gravity acts downward, which has a component in the -y direction and a component in the +x direction of this coordinate system. The correct sign is given in front of the force term in the equation. Do not also give 9.81 m/s2 a negative sign, or you will double count the direction. Note that 9.81 was used for g rather than 9.8, because three significant figures were given in the statement of the problem.
The coordinate system was chosen to be along the incline so that acceleration is one dimensional. ax = a
Only three significant figures were given in the text of the problem, so only three significant figures are included in the solution.
Notice that the sign of acceleration is the sign of the acceleration vector. a acts to the right and down along the incline. The fact that the child slows down comes about because the acceleration and initial velocity are in opposite directions.
----------------------------------------------------------------------------------------------
Step 2
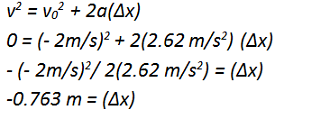
The child will travel 0.763 m downhill before coming to a stop.
1. Why is Δx negative?
The negative sign indicates direction—the final position is to the left of the initial position, as expected.
In this problem, up the hill was drawn up and to the left, or in the negative x direction. Therefore, the initial velocity of the sled is given a negative sign.
In this problem, the final velocity (v) is 0 and the starting velocity (v0) is 2 m/s to the left.
Remember that the sign on velocity is squared. Therefore, when you subtract this term from each side, you still have a negative sign.
The negative sign indicates direction—the final position is to the left of the initial position, as expected.

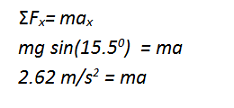
In this problem, the child and sled are on a slight hill. Therefore, gravity does not act directly into the surface. This is seen in the figure with two components of gravity—one into the hill and one along it. It is seen in the solution because the acceleration of the sled is less than that of gravity (less than the sled would have if it was in free fall.) The sign of acceleration indicates the direction of the vector and not whether or not the sled is slowing down or speeding up.
------------------------------------------------------------------------------------------
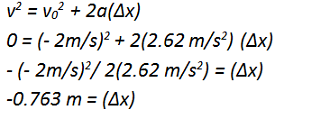
Because the acceleration is opposite to the sled’s initial motion, the sled slows down. When it reaches a stop, the child and sled have reached their maximum distance along the hill. The negative sign on Δx indicates the final position is to the left of the starting position.
- Why did you pick the coordinate system to be at the angle of the incline?
- How did you know where to put the 15.5o angle?
- My instructor taught us to rotate the FBD so that the y-axis is vertical. Why didn’t you do that?
- Why isn’t acceleration included on the free body diagram?
- Why isn’t there air resistance?
- Why isn’t buoyant force included on the free body diagram?
- Why did you focus on the child and sled together?
Why did you pick the coordinate system to be at the angle of the incline?
You can select any coordinate system that you want to use. However, the math will always be easier if you pick one axis to be in the direction of acceleration. In this case, acceleration is along the incline.
How did you know where to put the 15.5o angle?
There are two ways to approach this question. If you think visually, exaggerate the small and large angles on your drawing. In other words, 15.5o is less than half of a right angle, so draw the slope of the incline to be very small. Then you can see that mg makes a smaller angle with the –y axis than it does with the +x axis, and the smaller angle is 15.5o.
If you think geometrically, use the fact that the two small angles on a right triangle add up to 90o. The triangle on the first drawing made by the ground, the incline, and mg is a right triangle, so the angle between the incline (the +x axis) and mg must be (90-15.5)o=74.5o. It is equally fine to use the 74.5o angle, just note that sin and cos are reversed (because which side is opposite and which is adjacent depends on the triangle you draw.) You will get the same answer because sin(74.5o)=cos(15.5o).
I chose to use the first method simply because that is an easier way to determine the correct angle for most students.
My instructor taught us to rotate the FBD so that the y-axis is vertical. Why didn’t you do that?
Rotating the FBD picture is fine. It makes it easier for some people to visualize the x- and y-components of the gravitational force. Leaving the FBD oriented with the line of the incline is easier for other people to visualize how the forces relate to the motion of the sled. Use whichever orientation is better for you!
Why isn’t acceleration included on the free body diagram?
The free body diagram is a stylized drawing to help you visualize the cause of motion, and to directly map the drawing into the left hand side (ΣF) of Newton’s Second Law. Acceleration is the effect of the forces, and therefore is not included on the list of forces.
Why isn’t there air resistance?
There is! However, air resistance depends on velocity (squared) as well as on cross sectional area, and so at low speeds (such as for a sled) it is much smaller than the force of gravity on the child and sled and can therefore be ignored for the accuracy required in this problem.
Why isn’t buoyant force included on the free body diagram?
It is true that air puts a small buoyant force on the child and sled. However, the size of the upward buoyant force compared to the downward force of gravity is very small. (The ratio of the two is given by the ratio of the density of air to the density of the child and sled.) So to the number of significant figures included in this problem, we do not need to take buoyant force into account.
Why did you focus on the child and sled together?
The child and the sled move as a single system (the problem states that the child holds on and does not fall of the sled.) You are not asked for any of the forces between the child and the sled, and so you do not need to treat them separately.
