In order to paint the outside of your house, you buy a 24 ft aluminum extension ladder. The ladder weighs 61 pounds, and has rubber caps on the bottom of the legs. You put the base of the ladder on the sidewalk 7.5 feet from the side of your house. Can you safely climb all the way up the ladder? Assume that there is no friction with the side of the house.
-
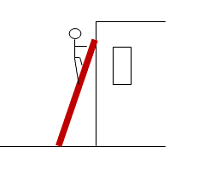
In order for you to climb the ladder safely, it must remain in place as you climb. In other words, you want the motion of the ladder to remain at rest both translationally and rotationally as the location of the forces on the ladder changes. Any time you compare forces and motion of an object, it is best understood through Newton's Second Law. Because you need to consider rotational as well as translational motion, you will need to work with the rotational equivalent of the law as well as with the linear version.
As you climb the ladder, the location of the force you put on the ladder changes. When the location of a force matters, we know that we need to consider torque. In order to be safe, the ladder must remain in place without slipping, and so both translational and rotational effects must balance.
My book refers to this as an equilibrium problem. Why do you call it a Second Law problem?
Equilibrium is just a special case of 2nd Law problems in which a = 0 (and α = 0). The value of acceleration does not affect the way you approach the problem.
-
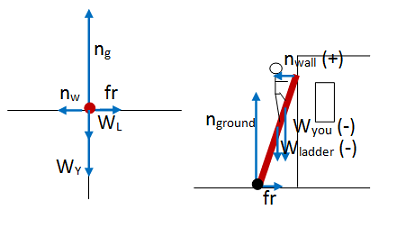
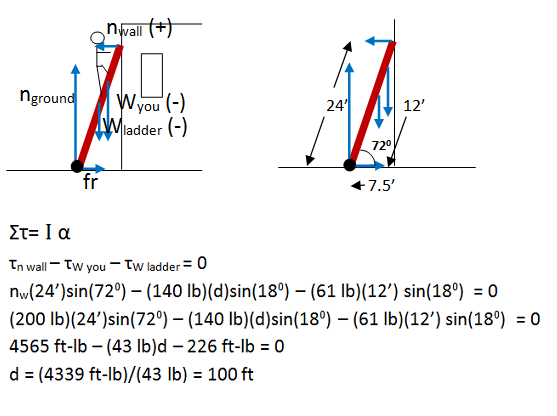
When we work with translational motion, we picture the action of forces with a free body diagram. When we work with rotational motion, the location of the forces also matters. Therefore, we need both a free body diagram and a picture showing the forces at the points where they act. If your drawing gets too cluttered, you can lable the geometric quantities on yet another drawing as shown below.
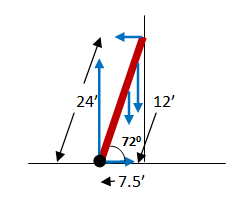
Why did you pick the axis of rotation at the bottom of the ladder?
Because the ladder does not rotate (it is in static equilibrium), the choice of axis is up to you. I chose it to be at the base of the ladder in part because that makes conceptual sense to me (I want the feet of the ladder to remain at rest), and in part because then neither the normal force of the ground nor the frictional force contribute to torque about the axis. I can eliminate two terms in my torque equation.
Don't you put a normal force on the ladder?
Yes, you push down on the ladder with the same force that it pushes up on you. If you think about your free body diagram, you realize that the ladder must push up on you with a force equal to your weight. Therefore, nyou on ladder = nladder on you = Weightyou.
Why didn't you pick your location to be 24' from the bottom of the ladder?
That is a perfectly acceptable approach to solving this problem. In that case, you would solve for the minimum coefficient of friction needed and compare that value to published values for friction between rubber and concrete.
The ladder weighs 61 lbs. Because it is a uniform object, you can take the force as acting at the center of the ladder, or 12 feet from the feet. As always, weight (gravitational force) acts straight down.
Because you are told to ignore friction with the wall of the house, the only force exerted by the wall on the ladder is the normal force. Make sure to label it well to distinguish it from the normal force that the sidewalk puts on the ladder. Normal force always acts straight out from a surface.
Because the ladder does not rotate (it is in static equilibrium), the choice of axis is up to you. I chose it to be at the base of the ladder in part because that makes conceptual sense to me (I want the feet of the ladder to remain at rest), and in part because then neither the normal force of the ground nor the frictional force contribute to torque about the axis. I can eliminate two terms in my torque equation.
cosθ = adj/hyp = (7.5'/24') = 0.3125. θ = cos-1 (0.3125) = 720. Not that some calculators use "inv cos" rather than "cos-1."
Your weight acts on the ladder at some unspecified distance. The question asks if you can climb the ladder safely all the way, and so one way to approach the problem is to solve for the greatest distance you can have from the base before the ladder slips.
If you labeled this force as a normal force due to you rather than your weight, that is fine. But then note that you push down on the ladder with the same force that it pushes up on you. If you think about your free body diagram, you realize that the ladder must push up on you with a force equal to your weight. Therefore, nyou on ladder = nladder on you = Weightyou.
For the question of translational motion, you just care about the net push or pull in any direction and so drawing the object of interest as a dot gives a nice "tug of war" visualization of the forces. Such a figure does not, however, help us visualize the cause of rotational motion.
Although no coefficient of friction was specified in the problem, you know that friction between rubber and concrete is too large to ignore. In any case, if friction wasn't present the ladder would slip as soon as you began to climb. Therefore, you know that the ground exerts both a normal force and a frictional force on the ladder. Normal force is always directed out from the surface and frictional force is along the surface to oppose sliding. If the ladder slides, the base will go left according to my drawing. Therefore, frictional force pulls to the right.
The direction of torque is perpendicular to the plane in which the object rotates. A counter-clockwise rotation is a +z direction torque (the thumb of your right hand comes out of the page if you curl your fingers CCW) and a clockwise rotation is a - z direction torque.
To determine the direction for any given torque, imagine putting a pin through the axis of rotation and pulling on the appropriate force arrow as if it were a string. If you pull, for example, on nwall, the top of the ladder will rotate to the left, or clockwise. If you pull on the ladder's weight, the top of the ladder will go right, or counterclockwise.
You are told in the problem that the ladder is 24' long. Make sure to measure that distance along the ladder and not along the wall. The normal force of the wall acts 24' from the axis.
-
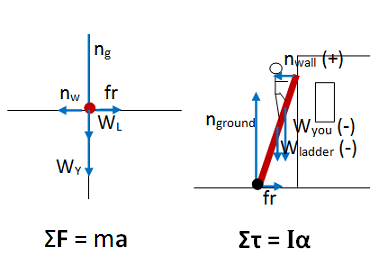
The key equation for any problem that relates forces and motion is Newton's Second Law. The left side of the equation takes into account the forces that act on the object, and the right side shows the effect of those forces. To examine rotational effect, we look at the torques on the object. To examine translational effect, we look at the forces on the object.
What if I only thought of this as a rotational problem?
If you begin the problem thinking about the rotation of the ladder and examine torques only, you will quickly see that you have an additional unknown in your equation. At that point, you will recognize that you also have to examine the balance of forces.
-
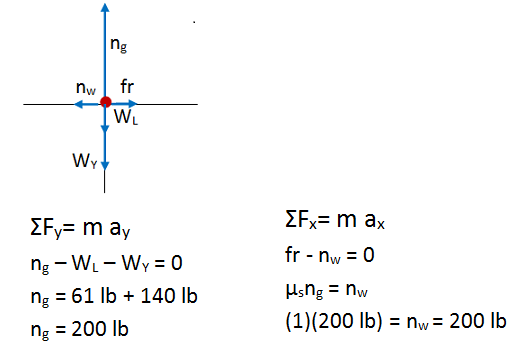
It does not matter if you begin this problem by examining force or torque. Past experience has shown me that it is often true that the force equations can be solved and the results used in the torque equation. However, beginning with torque is equally fine--scroll down to see that part of the solution.
Why did you use pounds instead of Newtons? Why didn't you include g in your calculation?
I was told weight rather than mass and so I did not need to multiply by g in order to calculate force. There is no need to convert to the metric system in this case. I can more easily specify my location on the ladder in terms of feet and work in the English system.
Why isn't a = 9.8 m/s2 (= 32 ft/s2)?
It is true that gravity acts on the ladder. That action appears as the weight of the ladder--as a force pulling on the ladder. Acceleration is the effect of all of the forces acting, and in this case the desired effect is that the ladder remain in place.
Although the coefficient of friction is not given in the statement of the problem, you know that the two surfaces of interest are rubber and cement. You can look up the coefficient of friction for different surfaces in your book or on the internet. Because you don't want the ladder to slip, make sure to look for the coefficient of static friction. I found values between 1 and 4 on my google search for the coefficient of static friction between rubber and dry cement. I chose to use 1 because a greater friction would allow me to climb further, so I am interested in the worst case in order to ensure that the ladder stays in place. Note that with this sort of estimation, it is silly to carry the weight of the ladder to two significant figures.
In this step, I added both weights to both sides of the equation, and so both should have a positive sign.
No weight is specified for "you" and so I chose a reasonable weight for a person. Obviously, if you choose a heavier weight, you will find a shorter distance over which your person can safely climb.
Because the weight of the person on the ladder is an estimate, it is meaningless to keep additional significant figures in the answer.
Remember, maximum static friction is equal to the coefficient of static friction between two surfaces times the normal force between those surfaces. Therefore, you want to use the normal force of the ground and not that of the wall.
You do not want the ladder to begin to move in any direction. Therefore, all components of acceleration are zero.
----------------------------------------------------------------------------------------------
Step 2
At this angle, and with these surfaces, you can safely climb a distance much longer than the length of the ladder. So yes, you can safely climb it.
How did you fill in for torques?
The amount of torque that a force exerts is given by the force times the distance it acts from the axis times the sign of the angle between force and the radius: τ = F r sinθ.
Why didn't you use 24'? The person wants to climb all the way up the ladder.
It is perfectly fine to put in the maximum distance climbed as d in this problem. In that case, you would solve for the required coefficient of static friction and compare your answer to published values.
I used 24' and my values on the two sides of the "=" sign don't agree. What did I do wrong?
Make sure that you don't also use the published value for the coefficient of static friction. Remember that static friction is a passive force--it has a maximum, but it's actual value depends on the other forces acting. You can approach this problem as I did, by seeing how far you could climb if friction acts at its maximum. You can also approach this problem by solving to find how much friction is required to climb all the way up (put in d and solve for friction and therefore minimum μ.) But don't put in both values. If you do, your numbers won't agree because in this case friction does not have to be at its maximum possible value in order to keep the ladder in place.
You want the ladder to stay in place. Therefore, the torques on the ladder need to cancel out. They must balance to zero.
If you imagine anchoring the ladder at the axis and pulling left (the direction of the normal force), the ladder rotates CCW or in the + direction.
If you imagine anchoring the ladder at the axis and pulling down (the direction of weight), the ladder rotates CW or in the - direction.
All forces acting at some distance r from the axis exert a torque on the ladder. In this case, you need to consider torques due to normal force of the wall, the weight of the ladder, and the weight of the person on the ladder.
Athough normal force of the ground and friction act on the ladder, they do not exert a torque about the anchor point with the ground. Each acts at a distance r = 0 from that point, and τ = F r sinθ.
cosθ = adj/hyp = (7.5'/24') = 0.3125. θ = cos-1 (0.3125) = 720. Note that some calculators use "inv cos" rather than "cos-1."
The angles of a triangle add to 1800. The two known angles in this triangle are 900 and 720. Therefore, the remaining angle (the angle that a vertical line makes with the ladder) is 180.
The angles of a triangle add to 1800. The two known angles in this triangle are 900 and 720. Therefore, the remaining angle (the angle that a vertical line makes with the ladder) is 180.
τ = F r sinθ In this case, the 200 N normal force acts all the way up the ladder (24') from the axis and makes a 720 angle with the ladder.
τ = F r sinθ In this case, your 140 lb weight acts some unknown distance up the ladder. If you trace along the ladder from the axis and down the weight arrow, you see that the angle between them is 180.
τ = F r sinθ In this case, the 61 lb weight of the ladder acts in the center of the ladder, or 12' from the axis. If you trace along the ladder from the axis and down the weight arrow, you see that the angle between them is 180.
-


In order for you to climb a ladder safely, the ladder needs to remain in place. There must not be any translational or rotational motion. This means that the forces on the ladder need to balance and also that the torques on the ladder need to balance. In this case, the ladder is on a rough surface and put fairly steeply in against the wall--it makes sense that forces and torques will balance.
You may also have noticed that very little information was provided. Be confident in your approach to the physics by clearly articulating why you approach the problem as you do. If you are confident that you are looking at the appropriate interactions, you can look up tabulated data that you need.
Finally, note that there are several ways to approach the problem. You can either use the maximum available friction to find how high you can climb, or you can find the friction needed to climb the length of the ladder. Both approaches will lead to the same conclusion.
Because your solution is independent of mass, it is not limited to only heavy vehicles like trucks.
(58 ft/s)(1 mi/5280 ft)(3600 s/hr) = 39 mi/hr
The problem doesn't give me much information. Where do I begin?
As always, focus on the key physics behind the situation. You can look up or estimate any numbers that you need once you understand how to approach the problem. In this case, you don't want the ladder to slip. In other words, you want it to remain in equilibrium both translationally and rotationally. It is a Second Law problem.
What are the conversions between feet and meters and between pounds and Newtons?
It doesn't matter. Why not just work the problem using English units?
Why do you focus on the ladder and not on "you"?
You know that if a ladder isn't well anchored it can slip if you climb too high. This is because the farther you push on the ladder from the pivot point, the more torque you exert on the ladder. It is the ladder that you want to remain at rest.
How do you know what forces to include?
Go to the Draw a Picture page for a full discussion of the forces on the ladder.
How do you know the directions of the torques?
Go to the Solve page for a full discussion of the direction of torque.
