A royal treasurer commissions a craftsman to make an elaborate gold crown. When the crown is delivered, she suspects that it may actually be made of brass covered in gold. She has the crown tested to make sure. The crown weighs 24.5 N in air, and has an apparent weight in fresh water of 22.1 N. Is the treasurer correct?
-
Even though most text books put buoyant force problems in a separate (fluids) chapter from Newton’s Laws, this is a Newton’s 2nd Law problem. You are told about forces (weight, apparent weight) on a crown and have the extra knowledge that we typically weight objects when they are at rest. In other words, you also know about the crown’s motion.
Force and motion of a single object are always related through Newton’s Second Law, so this is a force or 2nd Law problem regardless of what information is requested in the problem.
-
How will analyzing forces help me answer the question about whether or not the crown is pure gold?
If you don’t have a clear picture of how you will answer the question when you begin, that is ok. You don’t need to differentiate known from unknown quantities until you have set up the 2nd Law equations. You should always select your approach to a problem on the key interactions that are described, rather than the unknown quantities.
After you have the experience of doing several problems of this type, you will become more comfortable seeing the big picture: buoyant force depends on the submerged volume of an object, and so if you know mass and find the volume of the crown, you can determine its density (and therefore the material of which it is made.)Why isn’t acceleration shown on the figure?
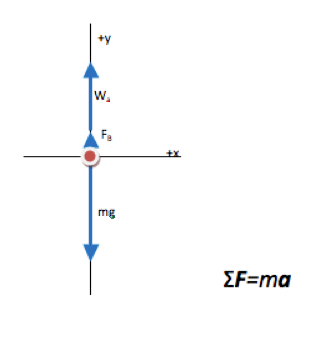
The free body diagram is a sketch of the forces on an object, or the causes of motion. Acceleration is the effect of those forces and therefore does not show up on the FBD. It will make an appearance in the equation.
How do you know to include buoyant force?
Although the problem does not explicitly state that buoyant force is present in a significant way, you know that it must be taken into account because the actual weight and apparent weight of the crown are noticeably different. The crown is in water, and there are no other forces acting on it, so buoyant force must be responsible for the difference.
As a general rule of thumb, liquids are dense enough that the buoyant force they put on objects needs to be included in 2nd Law analysis.Why is apparent weight directed upward? Isn’t weight a downward force?
Apparent weight is another way of saying “what the scale reads.” In this problem, you might picture a spring scale with the crown hanging from it in a vat of water as I drew, or you could picture the crown resting on the bottom of the vat on a bathroom scale. In either case, the scale acts to hold the crown up against the downward force of gravity.
My numbers are close but not exactly what is shown in the equation. Am I close enough?
Only three significant figures were given in the text of the problem, so only three significant figures are included in the solution.
How did you know what formula to fill in for buoyant force?
For a totally submerged object, buoyant force is an active force: its value does not depend on other forces present, but is always given by FB=ρVg. ρ is the density of the fluid that the object is in, V is the total volume of the object (because it is completely submerged), and g is 9.81 m/s2. The direction of buoyant force is taken into account as your write your equation, so the formula is just used for the value. In other words, all numbers are positive.
How did you know what numbers to fill in for buoyant force?
The density in the formula FB=ρVg is that of the fluid in which the object of interest is submerged. In this problem, the crown is submerged in water. You can find the density of water in a table in your text book or on the web.
Apparent weight is another way of saying “what the scale reads.” In this problem, you might picture a spring scale with the crown hanging from it in a vat of water as I drew, or you could picture the crown resting on the bottom of the vat on a bathroom scale. In either case, the scale acts to hold the crown up against the downward force of gravity.
All objects near Earth experience a downward force of gravity equal to mass of the object x 9.81 m/s2. Weight is another term for the force of gravity on an object (W=mg).
Although the problem does not explicitly state that buoyant force is present in a significant way, you know that it must be taken into account because the actual weight and apparent weight of the crown are noticeably different. The crown is in water, and there are no other forces acting on it, so buoyant force must be responsible for the difference.
As a general rule of thumb, liquids are dense enough that the buoyant force they put on objects needs to be included in 2nd Law analysis.In this problem, you were given weight rather than mass. Therefore, you did not need to multiply by 9.81 m/s2. (mg=W=24.5 N) The direction is down, which is represented by the negative sign in front of the term.

There is nothing in the statement of the problem to suggest that the crown is weighed in an accelerating environment. Therefore, the acceleration of the crown is zero.
For a totally submerged object, buoyant force is an active force: its value does not depend on other forces present, but is always given by FB=ρVg. ρ is the density of the fluid that the object is in, V is the total volume of the object (because it is completely submerged), and g is 9.81 m/s2. The direction of buoyant force is taken into account as your write your equation, so the formula is just used for the value. In other words, all numbers are positive.
For a totally submerged object, the volume in FB=ρVg is that of the entire object. In this case, the entire crown is under water.
The density in the formula FB=ρVg is that of the fluid in which the object of interest is submerged. In this problem, the crown is submerged in water. You can find the density of water in a table in your text book or on the web.
Only three significant figures were given in the text of the problem, so only three significant figures are included in the solution.
You were told the weight of the crown but not its mass. W=mg, so m=W/g.
What is apparent weight?
Apparent weight is what an object seems to weigh—the reading on a scale that supports the object. Apparent weight and weight (mg) are the same if the object is not accelerating and if there are no other vertical forces on the object. Unless otherwise stated in a problem, we assume that scales weigh objects when they are at rest. In this problem, apparent weight is different from actual weight because the upward buoyant force of the water helps to support the crown against the downward pull of gravity.
Why isn’t acceleration included on the free body diagram?
The free body diagram is a stylized drawing to help you visualize the cause of acceleration, and to directly map the drawing into the left hand side (ΣF) of Newton’s Second Law. Acceleration is the effect of the forces, and therefore is not included on the list of forces.
Shouldn’t I include the buoyant force of the air on the crown when I consider its weight in air?
Technically, yes. The scale reading of weight of the crown in air is slightly less than mg because of the upward buoyant force of the air. However, that force is very tiny compared to mg (the ratio of forces is the same as the ratio of the density of air to that of the crown) and so can be ignored to the accuracy of this problem.
Can I pick the +y direction to be down? Yes. In that case, weight would be in the +y direction, and buoyant force and apparent weight would be in the –y direction. Your answer will be the same in either case.
Why isn’t normal force included on the free body diagram?
Normal force is the contact force between two surfaces. It pushes out from the surfaces and keeps them from falling into each other. In this case, the crown is submerged in fluid, and the force due to the pressure of the fluid is called buoyant force. The crown is not resting on any surface. If you picture the crown on a bathroom scale rather than a spring scale, the “normal” force by the scale is already shown in the FBD as “Force by scale (apparent weight: Wa).” -
The key equation for any problem that relates forces and motion is Newton’s Second Law. Regardless of what quantity you are asked to find, begin with the Second Law. If additional information is needed, it will become apparent as you proceed.
-
Step 1


Newton’s 2nd Law allows you to solve for the volume of the crown, but does not yet tell you if it is pure gold. Continue to step 2 for the final step to answer the question.
-------------------------------------------------------------------------------------------
Step 2
At this point in the problem, you know that the crown weighs 24.5 N and has a volume of 2.45 x 10-4 m3. These two properties are related through the definition of density, and density can be used to identify a metal.
ρcrown = masscrown/volumecrown
ρcrown = (24.5 N/9.81 m/s2)/( 2.45 x 10-4 m3)
ρcrown = (2.50 kg)/( 2.45 x 10-4 m3) = 10,200 kg/m3
Using a table from your text book or from the web, you can find that the density of gold is 19,300 kg/m3, so the crown is definitely not pure gold. The density of brass ranges around 8300-8700 kg/m3 (remember brass is an alloy) and so it is entirely possible that this is largely a brass crown covered in gold. The treasurer is right that the crown isn’t gold, and her guess of its actual composition is reasonable.
What is apparent weight?
Apparent weight is what an object seems to weigh—the reading on a scale that supports the object. Apparent weight and weight (mg) are the same if the object is not accelerating and if there are no other vertical forces on the object. Unless otherwise stated in a problem, we assume that scales weigh objects when they are at rest. In this problem, apparent weight is different from actual weight because the upward buoyant force of the water helps to support the crown against the downward pull of gravity.
Why isn’t acceleration included on the free body diagram?
The free body diagram is a stylized drawing to help you visualize the cause of acceleration, and to directly map the drawing into the left hand side (ΣF) of Newton’s Second Law. Acceleration is the effect of the forces, and therefore is not included on the list of forces.
Shouldn’t I include the buoyant force of the air on the crown when I consider its weight in air?
Technically, yes. The scale reading of weight of the crown in air is slightly less than mg because of the upward buoyant force of the air. However, that force is very tiny compared to mg (the ratio of forces is the same as the ratio of the density of air to that of the crown) and so can be ignored to the accuracy of this problem.
Can I pick the +y direction to be down?
Yes. In that case, weight would be in the +y direction, and buoyant force and apparent weight would be in the –y direction. Your answer will be the same in either case.
Why isn’t normal force included on the free body diagram?
Normal force is the contact force between two surfaces. It pushes out from the surfaces and keeps them from falling into each other. In this case, the crown is submerged in fluid, and the force due to the pressure of the fluid is called buoyant force. The crown is not resting on any surface. If you picture the crown on a bathroom scale rather than a spring scale, the “normal” force by the scale is already shown in the FBD as “Force by scale (apparent weight: Wa).”
No. Rotational kinematics is appropriate if you wish to describe the motion around the circle, but it does not provide information about the cause of that motion.
The free body diagram is a sketch of the forces on an object, or the causes of motion. Acceleration is the effect of those forces and therefore does not show up on the FBD. It will make an appearance in the equation.
If you don’t have a clear picture of how you will answer the question when you begin, that is ok. You don’t need to differentiate known from unknown quantities until you have set up the 2nd Law equations. You should always select your approach to a problem on the key interactions that are described, rather than the unknown quantities.
After you have the experience of doing several problems of this type, you will become more comfortable seeing the big picture: buoyant force depends on the submerged volume of an object, and so if you know mass and find the volume of the crown, you can determine its density (and therefore the material of which it is made.)The density in the formula FB=ρVg is that of the fluid in which the object of interest is submerged. In this problem, the crown is submerged in water. You can find the density of water in a table in your text book or on the web.
Only three significant figures were given in the text of the problem, so only three significant figures are included in the solution.
-

ρ = mass/volume
ρcrown = (2.50 kg)/( 2.45 x 10-4 m3) = 10,200 kg/m3≠ ρgold
Regardless of what you were asked to find, this is a Newton’s Second Law problem, because the interactions that are described in the problem are forces acting on the crown. When the crown is submerged, water acts to push up on it. (It doesn’t float because the density of the crown is so much greater than that of water.) Therefore, it appears to weigh less than its actual value of mg. The downward force of gravity is exactly balanced by the upward force of the water plus that of the scale.
This information allows us to solve for the only unknown in the problem—that of the volume of the crown. The problem, however, asked us to determine if the crown is made of pure gold, and that identification can be made through density. Density is directly related to volume through a simple definition:

