University of Wisconsin Green Bay

• 
• Problems
• Dynamics
• Buoyant Force Problem: Boat With Cargo

Two children (with masses of 32 kg and 35 kg) are pretending to be pirates on a wooden raft in a freshwater lake. The raft is 1.8 m x 2.0 m x 0.18 m and it is made of pine which has a density of about 560 kg/m3. If the children hang two 25 kg “treasure chests” underneath the raft, will they get their feet wet? Each chest has a volume of 0.021 m3.

• Identify
• Draw a Picture
• Select the Relation
• Solve
• Understand

• In this problem, you are asked to determine whether or not the children will get their feet wet. This depends, of course, on whether or not the raft will sink—in other words, on whether or not it is buoyant enough to float while carrying the children and the chests. So with a little thought, you can see that you are asked to relate motion (the floating or sinking of the raft and its occupants and cargo) to force (buoyant force).
  
  Force and motion of a single object are always related through Newton’s Second Law, so this is a force or 2nd Law problem.

  
  

  • View Queries
• 
  

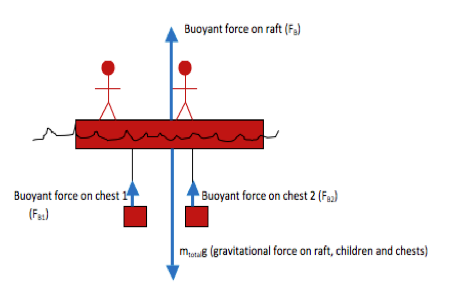
  Note that there is a great deal of detail in this problem. You don’t need to worry about any of the numbers (masses, densities, volumes, etc.) until you actually fill into the algebraic equation that comes out of Newton’s 2nd Law. At this stage, you only want to identify the best system to consider and the types and directions of forces on that system.

  
  

  • View Queries

  Forces aren’t mentioned anywhere in this problem. How should I know to relate floating or sinking to force?

  This is a case where experience solving many problems helps to identify the key interaction you need to approach a problem successfully. As a general rule as you build that experience, if you have an object floating or sinking in a fluid (including, for example, things like hot air balloons in air) you should begin by asking if you know enough about forces to approach the problem with Newton’s 2^nd Law.

  Why did you treat the raft, children and chests as a single system?

  In this case, the raft, the children, and the chests are all floating (or sinking) together as a single object. We are not asked any questions about the internal forces between them (for example, the normal forces between the children and the raft or the tension in the ropes.) The only question that is asked (essentially, will the raft float) can be most easily answered by looking at the system as a whole because it depends on the mass and volume of the system as a whole.

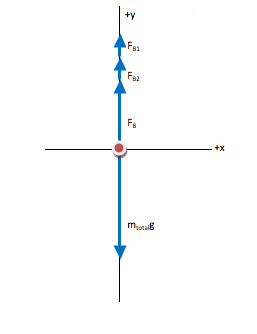
  You treated the gravitational force together as m_totalg, but you broke the buoyant force into three pieces (F_B, F_B1, and F_B2). Why didn’t you also treat the buoyant force as a single force?

  You absolutely can! It is set up this way only for convenience in calculations—we know that the chests are entirely submerged but we don’t know about the raft, and so by breaking out the buoyant force on the individual pieces of the object I will have one less step in the algebra at the end. The best way to set this up, however, is to draw the buoyant force on the free body diagram in whichever of these two ways makes the most sense to you. The algebra will take care of itself.

  How did you know acceleration is zero?

  In this case, we don’t know whether the raft is floating or sinking. The easiest way to approach the problem is to assume that it is floating, which means to assume that acceleration is zero. We can then solve for the volume of the raft that must be submerged in order for the system to float, and compare it to the total volume of the raft.
  
  If it makes more sense to you, it is equally fine to fill the entire volume of the raft into the F_B and solve for the resulting acceleration. In this case, you will find that a is positive or up. In other words, if you submerged the entire raft it will accelerate back up to the surface.

  How did you determine the mass of the raft?

  We were not told the mass of the raft, but we do know its dimensions and density, so it is merely a definition side problem to solve for mass.
  
  ρ = m/V
  m = ρV = (560 kg/m³)(1.8 m)(2.0 m)(0.18 m) = 360 kg

  My numbers are close but not exactly what is shown in the equation. Am I close enough?

  Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.

  The raft and chests are in a fluid (fresh water) which has a significant density when compared to densities of people, wood, etc. Therefore, you know that buoyant forces on all parts of the system in the fluid need to be considered.

  In this problem, we know that the chests are entirely submerged but we don’t know about the raft. By breaking out the buoyant force on the individual pieces (buoyant force on the raft, buoyant forces on the two chests) rather than treating it as a single buoyant force, there will be one less step in the algebra at the end. However, it is perfectly fine to draw a single buoyant force on this system. Just remember when you fill into the equations that the submerged volume of the object will include the volume of the two chests as well as the submerged portion of the raft.

  All objects near Earth experience a downward force of gravity equal to mass of the object x 9.8 m/s². This is true even if they are floating. Floating merely means that the downward force of gravity is balanced by the upward buoyant force of the fluid.
  
  In this case, I identified the gravitational force as being the total weight of the raft, the children, and the chests together as a single object. It is perfectly fine to break out the gravitational force as the weight of the raft plus the weight of each child plus the weight of each chest and draw them as separate arrows.

  In this case, we don’t know whether the raft is floating or sinking. The easiest way to approach the problem is to assume that it is floating, which means to assume that acceleration is zero. We can then solve for the volume of the raft that must be submerged in order for the system to float, and compare it to the total volume of the raft.
  
  If it makes more sense to you, it is equally fine to fill the entire volume of the raft into the F_B and solve for the resulting acceleration. In this case, you will find that a is positive or up. In other words, if you submerged the entire raft it will accelerate back up to the surface.

  Newton’s Law refers to the entire system you are examining. In this case, you have a raft with two chests and two children as your system, and so the mass of the system is the mass of all of those pieces.

  Buoyant force is the upward force of the fluid on an object. It is equal to the weight of the displaced fluid.
  
  F_B= W = m_{fluid displaced} g F_B = (ρ_fluidV_displaced)g = m_fluidV_submergedg
  
  Make sure you do not use the density of the object and the total mass, as that would give you the weight of the object not the weight of the displaced fluid.

  We were not told the mass of the raft, but we do know its dimensions and density, so it is merely a definition side problem to solve for mass.
  
  ρ = m/V
  m = ρV = (560 kg/m³)(1.8 m)(2.0 m)(0.18 m) = 360 kg

  Fresh water has a density of 1000 kg/m³. If you don’t know this number, check for a table of densities in your book or on the web.

  Because g appears in all terms, I divided it out to save the math. It is fine to leave it in, solve for F_B, and then divide by density of water and g to solve for the submerged volume.

  You might wonder if the chests are entirely under water as the problem implies, or if they are floating themselves. If the chests are denser than water, they will be entirely submerged, so you just need to calculate the density of the chests:
  
  ρ = m/V = 25 kg/0.021 m³ = 1200 kg/m³ > 1000 kg/m³

• 

  ΣF=ma

  
  
  

  The key equation for any problem that relates forces and motion is Newton’s Second Law. Regardless of what quantity you are asked to find, begin with the Second Law. If additional information is needed, it will become apparent as you proceed.

  
  
• 
  

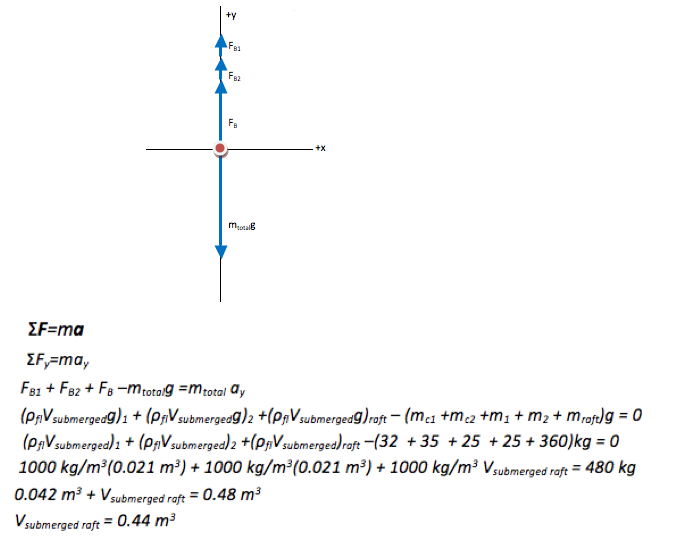
  At this point, we can say that if the raft has a volume of at least 0.44 m³, the raft and chests will displace enough water for the entire system to float. The total volume of the raft is (1.8 m x 2.0 m x 0.18 m) = 0.65 m³, so the raft will float and the children will not get their feet wet.
  
  Although no further information is requested in this problem, some similar problems will ask you to go a step further and determine how much of the raft is above water, which just requires one additional step to divide out the area.

  
  
  • View Queries

  To get to this line, I divided every term by 1000 kg/m³. The unit calculation is then kg/(kg/m³) or kg (m³/kg) which gives m³. Remember, to divide by a fraction, you invert and multiply.

  All forces on this object act vertically. Therefore, this is a one-dimensional problem and only needs to be solved in the y-direction.

  Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.

  V = length x width x height
  0.44 m³ = 1.8 m x 2.0 m x height
  height = 0.12 m
  
  In other words, 12 cm of the raft are submerged in this situation, leaving (0.18 m – 0.12 m) = 6 cm of the raft above water.

  Why did you treat the raft, children and chests as a single system?

  In this case, the raft, the children, and the chests are all floating (or sinking) together as a single object. We are not asked any questions about the internal forces between them (for example, the normal forces between the children and the raft or the tension in the ropes.) The only question that is asked (essentially, will the raft float) can be most easily answered by looking at the system as a whole because it depends on the mass and volume of the system as a whole.

  You treated the gravitational force together as m_totalg, but you broke the buoyant force into three pieces (F_B, F_B1, and F_B2). Why didn’t you also treat the buoyant force as a single force?

  You absolutely can! It is set up this way only for convenience in calculations—we know that the chests are entirely submerged but we don’t know about the raft, and so by breaking out the buoyant force on the individual pieces of the object I will have one less step in the algebra at the end. The best way to set this up, however, is to draw the buoyant force on the free body diagram in whichever of these two ways makes the most sense to you. The algebra will take care of itself.

  Why isn’t normal force included on the free body diagram?

  Normal force is the contact force between two surfaces. It pushes out from the surfaces and keeps them from falling into each other. In this case, the raft and the chests are in a fluid, and the force due to the pressure of a fluid is called the buoyant force. There will only be a normal force in this problem if you discover that the raft sinks and ultimately rests on the bottom surface of the lake.

  Why didn’t you include a buoyant force on the children?

  If the raft stays afloat, no part of the children will be under water and so the water will not exert a force on them.

  Why isn’t acceleration included on the free body diagram?

  The free body diagram is a stylized drawing to help you visualize the cause of acceleration, and to directly map the drawing into the left hand side (ΣF) of Newton’s Second Law. Acceleration is the effect of the forces, and therefore is not included on the list of forces.

  This is a case where experience solving many problems helps to identify the key interaction you need to approach a problem successfully. As a general rule as you build that experience, if you have an object floating or sinking in a fluid (including, for example, things like hot air balloons in air) you should begin by asking if you know enough about forces to approach the problem with Newton’s 2nd Law.

• 
  
  
  
  
  
  
  
  
  
  
  
  

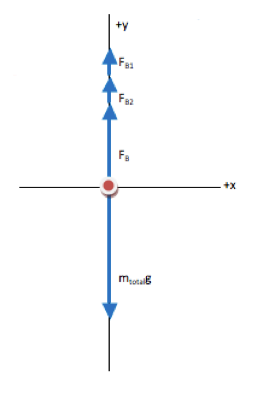
  ΣF=ma
  ΣF_y=ma_y
  F_B1 + F_B2 + F_B –m_totalg = 0

  
  
  
  
  
  
  
  

  In this problem, the upward buoyant force of the water acts against the downward weight of the raft, the children, and the chests. Buoyant force depends on the density of the fluid and the volume of fluid that is displaced by the object in it. Part of the raft and all of the chests are under water, and so the buoyant force depends on the total volume of the chests as well as the submerged volume of the raft.
  
  We were not told if the raft is able to float. By assuming a floating raft (a = 0) we could solve for the volume of the raft that would be required to stay afloat. That volume shows up in buoyant force on the raft (F_{B raft} = ρ_fluidV_{submerged part of the raft} g) and was found to be less than the total volume of the raft and so it is able to stay afloat.

  
  

• FAQs