A bullroarer is a device that was used by Native Americans, Aboriginal Australians and others as a tool for communication. It consists of a thin piece of wood tied to the end of a cord, and if it is whirled around in a circle while the wooden piece is also spinning, it makes a loud humming sound. If you make a bullroarer using a 0.065 kg piece of wood, and whirl it over your head in a horizontal circle so that it makes 2.5 revolutions every second, what is the angle that the cord makes with the horizontal? Assume that the radius of the circle is 1.2 m. What is the tension in the cord?
-
In this problem, you are asked to relate motion (the bullroarer moves in a circle) to force (tension). Force and motion of a single object are always related through Newton’s Second Law, so this is a force or 2nd Law problem.
If the problem only asked for the angle made by the rope, and therefore did not mention tension or any other force explicitly, after a little bit of thought you should still recognize this as a Second Law problem. Moving in a circle requires an inward force—in this case, tension, which is directed along the same direction as the rope.
As a general rule of thumb, if an object is moving in a uniform (constant speed) circle, forces are most likely to be the interactions that allow you to understand the problem in the most straightforward way.
-
Step 1
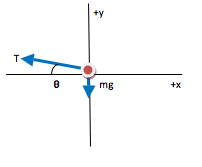
Your FBD is not yet finished, because tension has both x- and y- components. Continue down to step 2 when you are ready to continue.
----------------------------------------------------------------------------------------------
Step 2
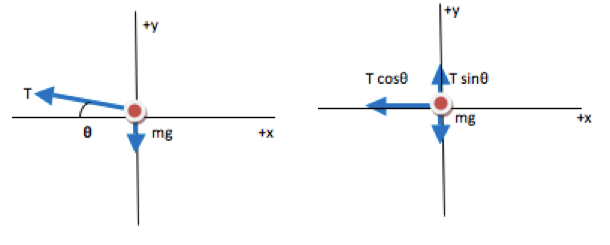
In the final FBD drawn here, all forces are divided into components. The contribution each force makes in the x-direction (in the plane of the circle) is shown explicitly, as is the contribution each force makes in the y-direction. The FBD is now a visual representation of ∑F=ma in each direction.
Can this problem be worked using rotational kinematics?
No. Rotational kinematics is appropriate if you wish to describe the motion around the circle, but it does not provide information about the cause of that motion.
Why isn’t acceleration shown on the figure?
The free body diagram is a sketch of the forces on an object, or the causes of motion. Acceleration is the effect of those forces and therefore does not show up on the FBD. It will make an appearance in the equation.
Why did you choose the +x axis to be to the left?
The direction of acceleration of an object moving in a uniform circle is always inward along the radius of the circle. As the drawing is shown, inward is to the left and so that choice for the +x axis would give you a positive direction for acceleration (and for tension.)
Isn’t the rope horizontal?
No. Gravity is pulling the wooden piece down, and so if it is moving in a horizontal circle (and not falling) there must be some force holding it up. The only other significant force in this situation is the tension in the cord, and therefore tension must have a component to balance gravity.
Why isn’t centripetal force shown on the diagram?
Knowing that the object moves in a circle gives you a great deal of information. It tells you that there is net inward force of just the right size to provide an inward acceleration equal to mv2/r.
Note that "centripetal force" should more properly be called "net inward force," because just refers to the fact that you need an inward force (forces that you already know, like friction or normal force or tension) in order to move in a circle. In this case, tension provides that inward force. If you were to also include a vector for centripetal force, you would double count the effect of tension.How did you divide tension into its components?
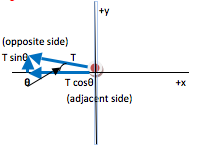
As you can see in the figure, the x- and y-components of a vector make up the sides of a right triangle. The vector itself forms the hypotenuse (h). The side of the triangle opposite the angle that you use is given by h sinθ and the side that touches the angle you use is given by h cosθ (soh cah toa)
In this case, the x-component is adjacent to θ and so is given by T cosθ as shown. Likewise, the y-component is opposite to θ and is therefore given by TT sin θ.Why is v2/r negative?
Acceleration of an object moving in a circle at a constant speed is inward toward the center of the circle (the negative x-direction as the drawing is shown here) and has a magnitude of v2/r.
How did you know acceleration in the y-direction is zero?
Acceleration of an object moving in a circle at a constant speed is inward toward the center of the circle, which is in the x-direction. The wooden piece on the end of the bullroarer neither rises nor falls, so there is no changing motion, and therefore no acceleration, in the y-direction.
I don’t get the same answer as you. Are my numbers close enough?
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
Knowing that the object moves in a circle gives you a great deal of information. It tells you that there is net inward force of just the right size to provide an inward acceleration equal to mv2/r.
Note that "centripetal force" should more properly be called "net inward force," because just refers to the fact that you need an inward force (forces that you already know, like friction or normal force or tension) in order to move in a circle. In this case, tension provides that inward force. If you were to also include a vector for centripetal force, you would double count the effect of tension.Tension is the result of the molecular attractions in the cord holding the cord together. Therefore, it always acts toward the center of a cord. The cord in this case cannot be horizontal, because in addition to pulling the piece of wood inward it also holds the wood up against gravity. In other words, it has both x- and y-components.
All objects near Earth experience a downward force of gravity equal to mass of the object x 9.8 m/s2. In this case, the piece of wood is not falling. Therefore it must be held up against gravity by tension in the rope. In other words, because you know there is gravity on the piece of wood, you also know tension has a y-component.
You do not need this information at this time. Once you have established that this is a Second Law Problem (see the Identify page), you know that only information about forces is included on the Free Body Diagram. This will be useful information when you solve the problem mathematically but does not affect how you draw the FBD.

As you can see in the figure, the x- and y-components of a vector make up the sides of a right triangle. The vector itself forms the hypotenuse (h). The side of the triangle opposite the angle that you use is given by h sinθ and the side that touches the angle you use is given by h cosθ (soh cah toa)
In this case, the x-component is adjacent to θ and so is given by T cosθ as shown. Likewise, the y-component is opposite to θ and is therefore given by TT sin θ.The x-component of tension is inward towards the center of the circle. That is the negative x-direction as the drawing is shown here.
Acceleration of an object moving in a circle at a constant speed is inward toward the center of the circle (the negative x-direction as the drawing is shown here) and has a magnitude of v2/r.
Acceleration of an object moving in a circle at a constant speed is inward toward the center of the circle, which is in the x-direction. The wooden piece on the end of the bullroarer neither rises nor falls, so there is no changing motion, and therefore no acceleration, in the y-direction.
Speed is defined as distance/time. In the case of the wooden piece at the end of the cord,
v = 2.5 x around the circle/1 second
v = 2.5 (2πr)/1 s
v = 2.5 (2π)(1.2 m)/1 s
v = 19 m/sOnly two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
-
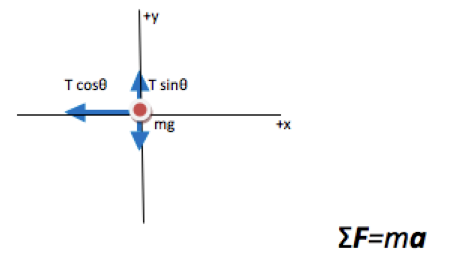
The key equation for any problem that relates forces and motion is Newton’s Second Law. Regardless of what quantity you are asked to find, begin with the Second Law. If additional information is needed, it will become apparent as you proceed.
-
Step 1
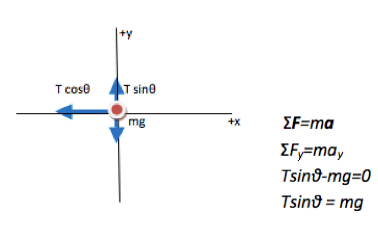
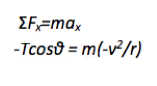
At this point, it seems that you have two equations and three unknowns (T, θ, and v). Values for m and r are specified in the problem. But the problem also states that the bull-roarer makes 2.5 revolutions every second, which is an indirect way of specifying velocity. (Click here to see the velocity calculation.) So you actually have two equations in two unknowns. Scroll down to Step 2 to continue the mathematical solution.
----------------------------------------------------------------------------------------------
Step 2
At this stage in the problem, we have two unknowns, θ and T, and two unsolved equations:
-Tcosθ = m(-v2/r)
Tsinθ = mg
One approach that always works is to solve one equation for one of the variables and substitute it into the other.

Now that you have solved for one of the unknown variables, substitute it into either of the original equations to solve for the other variable. I will substitute it into the second equation.
T sin(1.90) = mg
T = (0.065 kg)(9.8 m/s2)/ sin(1.90)
T = 20. N
Tension in the cord and angle of the blocks are the only information requested in this problem. No further mathematical solution is necessary.
Why isn’t acceleration included on the free body diagram?
The free body diagram is a stylized drawing to help you visualize the cause of acceleration, and to directly map the drawing into the left hand side (ΣF) of Newton’s Second Law. Acceleration is the effect of the forces, and therefore is not included on the list of forces.
Can I pick the +x direction to be to the left?
Yes. The direction of acceleration of an object moving in a uniform circle is always inward along the radius of the circle. As the drawing is shown, inward is to the left and so that choice for the +x axis would give you a positive direction for acceleration (and for tension.)
Isn’t the rope horizontal?
No. Gravity is pulling the wooden piece down, and so if it is moving in a horizontal circle (and not falling) there must be some force holding it up. The only other significant force in this situation is the tension in the cord, and therefore tension must have a component to balance gravity.
Why isn’t normal force included on the free body diagram?
Normal force is the contact force between two surfaces. It pushes out from the surfaces and keeps them from falling into each other. In this case, the bull-roarer is not resting on any surface.
Why isn’t there air resistance?
There is! However, air resistance depends on velocity (squared) as well as on cross sectional area, and so at low speeds it is likely to be small enough to ignore.
Why isn’t buoyant force included on the free body diagram?
It is true that air puts a small buoyant force on the wood. However, the size of the upward buoyant force compared to the downward force of gravity is very small. (The ratio of the two is given by the ratio of the density of air to the density of wood.) So to the number of significant figures included in this problem, we do not need to take buoyant force into account.
No. Rotational kinematics is appropriate if you wish to describe the motion around the circle, but it does not provide information about the cause of that motion.
The free body diagram is a sketch of the forces on an object, or the causes of motion. Acceleration is the effect of those forces and therefore does not show up on the FBD. It will make an appearance in the equation.the cause of that motion.
-
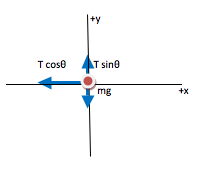
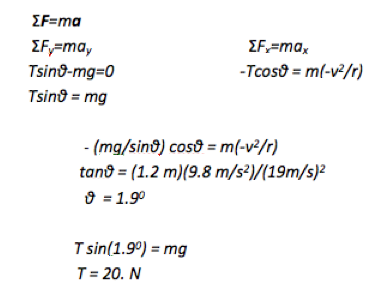
As summarized in Newton’s First Law, if there is no net force on an object it will move in a straight line at a constant speed. In this case, although the speed of the wooden piece is constant, its direction is not. Therefore, we know that there is a net force on it. Whenever motion of an object is in a circle, we further know that the net force must be exactly strong enough to provide an inward acceleration of v2/r, where v is the speed of the object around the circle and r is the radius of that circle.
In this problem, it is the horizontal component of tension which provides the inward net force. In addition, the cord must angle slightly below the horizontal in order to also have an upward component to balance the gravitational force.
Mathematically, there were several extra steps in solving this problem. It is frequently true that a problem will describe revolutions, for example, rather than giving speed. As long as you are confident in your basic approach to the problem (Newton’s Second Law) the problem will steer you towards those side steps. In this case, when it came time to fill in numbers, you recognized that revolutions/time is related to speed.
