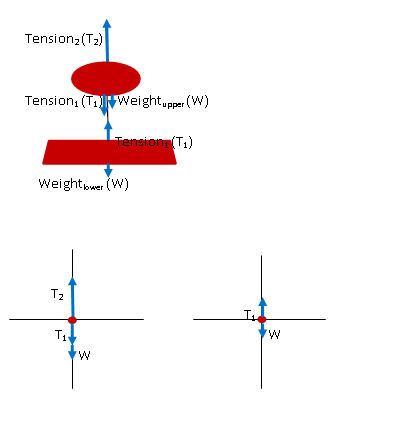
You are designing a lamp for the interior of a special executive express elevator in a new office building. The lamp has two sections that hang one directly below the other. The bottom section is attached to the top one by a single thin wire and the upper section is attached to the ceiling by another single thin wire. Because the idea is to make each section appear to be floating without support, you want to use the thinnest (and thus weakest) wire possible. You decide to calculate the force each wire must exert on the lamp sections in case of an emergency stop. The elevator has all the latest safety features and will stop with an acceleration of g/3 in any emergency. Each section of the lamp weighs 7.0 N.
This problem was used with permission of Dr. Ken Heller of the University of Minnesota Physics Education Research Group.
-
In this problem, you are asked to relate motion (the acceleration of the lamp) to force (tension, or strength of the wire). Force and motion of an object are always related through Newton's Second Law, so this is a force or 2ndLaw problem.
In this case, you are asked not only about the tension in the top wire but also the tension in the wire between the two parts of the lamp, so this is a two object problem. If you don't see the need for two objects at this stage, it will become apparent when you draw the picture.
Wires, ropes, strings, etc. all act through the force of tension. Because tension is a passive force, its value depends on the motion of the objects and the other forces present. But all passive forces have a maximum value or "breaking point." So when you are asked about the strength of a wire, you are really asked about the maximum force, or tension, it can exert.
The problem tells me to calculate force. How would I know to do so if that wasn't spelled out?
Wires, ropes, strings, etc. all act through the force of tension. Because tension is a passive force, its value depends on the motion of the objects and the other forces present. But all passive forces have a maximum value or "breaking point." So when you are asked about the strength of a wire, you are really asked about the maximum tension it can exert.
-
Why isn't acceleration shown on the figure?
The free body diagram is a sketch of the forces on an object, or the causes of motion. Acceleration is the effect of those forces and therefore does not show up on the FBD. It will make an appearance in the equation, and you can certainly draw it to the side if you wish.
Why did you choose down to be negative?
The choice of coordinate system is entirely your own. The math is always easier if you choose one axis along the direction of acceleration, which in this situation is vertical. I typically choose down to be negative, but if you chose it to be positive you will still get the same answer. Just remember to reverse the signs on all vertical forces.
Why doesn't the weight of the lower portion of the lamp show up on the drawing of the upper portion? I know that the lower portion of the lamp pulls down on it!
You are right - the lower portion of the lamp pulls down on the upper piece. However, that pull is communicated to the top piece through the tension in the lower wire. All the top piece knows is that the wire pulls down on it. If you also include the weight of the bottom piece, you will double count that effect.
Why did you draw the forces on the two parts of the lamp separately and not on the lamp as a whole?
You could certainly do that, and doing so would allow you to find the tension in the upper wire.
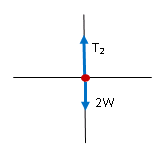
However, at some point you would realize that the information about the middle wire is lost and so you would also need a free body diagram for the lower piece.
Wires, strings, and ropes exert forces on objects through the force of tension. The direction of tension is always in from the ends of a wire towards the center. Therefore, the upper wire pulls up on the lamp.
Wires, strings, and ropes exert forces on objects through the force of tension. The direction of tension is always in from the ends of a wire towards the center. Therefore, the lower wire pulls up on the bottom part of the lamp and down on the top of the lamp. Note that I gave it the same symbol (T1) because the magnitude of the tension throughout a light wire will be the same.
If you drew the lamp as a single object as shown below, you would lose all information about the strength of the lower wire and so T1 would not appear in your drawing. At this point you should recognize that you need a second free body diagram for the lower portion of the lamp.

If you drew the lamp as a single object rather than as two objects, you would lose all information about the strength of the lower wire and so T1 would not appear in your drawing. At this point you should recognize that you need a second free body diagram for the lower portion of the lamp showing the action of T1 - in other words, that this is a two object problem. You can either treat the lamp as a lower portion and an upper portion as I did here, or you can treat it as a single object to find the tension of the top wire and examine just the lower section to find the tension in the bottom wire.
The free body diagram is a sketch of the forces on an object, or the causes of motion. Acceleration is the effect of those forces and therefore does not show up on the FBD. It will make an appearance in the equation, and you can certainly draw it to the side if you wish.
Weight is the measure of the gravitational force on an object. Although you know that the weight of the lower portion of the lamp affects the tension in the top wire, you do not include the weight of the lower portion on the FBD of the upper portion because that information is communicated to the upper wire through the action of the tension in the lower wire. Including both weights on the FBD of the upper part of the lamp double counts the effect.
-
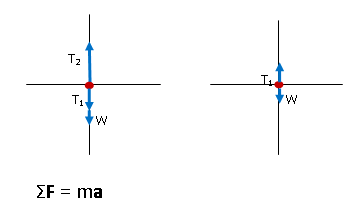
The key equation for any problem that relates forces and motion is Newton's Second Law. The left side of the equation takes into account the forces that act on the object, and the right side shows the effect of those forces. Regardless of what quantity you are asked to find, begin with the Second Law. If additional information is needed, it will become apparent as you proceed.
There are two objects of interest in this problem. How does the equation apply to that situation?
Newton's Second Law relates the forces on a single system to the motion of that system. Because you have two systems of interest in this problem, you will need to apply the equation to each part of the lamp individually. You cannot add all of the forces on both systems together into a single equation--in this case, you would lose all information about tension in the lower wire.
The Σ in this case refers to the sum of forces on a single system. Therefore, you will use the equation twice--once for the top portion of the lamp and again for the lower piece.
-
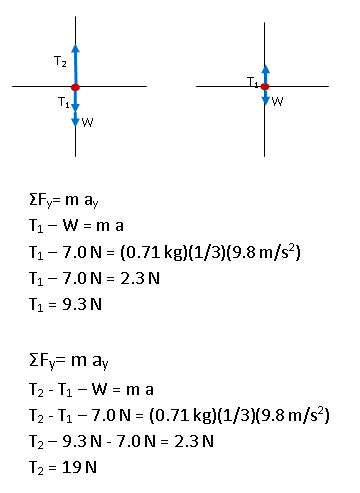
The upper wire must be able to exert a force of at least 19 N. The lower wire must be able to exert a force of at least 9.3 N.
Why is 9.8 m/s2 positive?
For the greatest tension in the wires, acceleration must be up (or + as I have chosen my coordinate system.) Therefore, a=(1/3)(+g).
I just multiplied the weight of the lamp by 1.33 to find the answer. Is that ok?
If you recognized that an upward acceleration of 1/3 g would act as a 33 percent increase in the weight of the object, that is fine. However, it is a good idea to practice your problem solving on straightforward examples so that you are comfortable with the approach in cases where you can't see the final answer from the start.
What if I treated the lamp as a single system?

In that case, your equation would read
T2 - 2W = 2(0.71 kg)(1/3)(9.8 m/s2)
and you would calculate the same answer for T2. You would need to work the equation for the lower portion of the lamp as shown in order to calculate T1.Each portion of the lamp has a weight, or gravitational force, of 7.0 N. Because the weight was already given in N, you did not need to multiply it by g. Note that the weight acts downward and so is subtracted in the equations.
You are told that the vertical acceleration has a maximum value of g/3, or (1/3)(9.8 m/s2). If you have not been sure about the sign of acceleration up to this point, you can see it now--a positive acceleration requires a greater tension and so you want to solve for the +a case. This makes sense--with an upward acceleration, the wire must entirely support the lamp against gravity and also provide an additional upward pull.
Two significant figures were given in the statement of the problem and so two significant figures are included in the solution.
The tension throughout the lower wire has about a constant value because the wire is light. It was given the same symbol, T1, to reflect that. Note that recognizing this fact reduces the number of unknowns in your equations. You may also think of this as Newton's Third Law--the upper and lower pieces of the lamp pull on each other with the same magnitude force. As always, I represented the downward pull with a negative sign and the upward pull with a positive.
Because you were told weight and not mass, you will need to calculate mass.
W = mg so m = W/g = (7.0 N)/(9.8 m/s2) = 0.71 kg.
The only forces acting in this situation are vertical, and so you only need to apply Newton's Law in the y-direction.
-
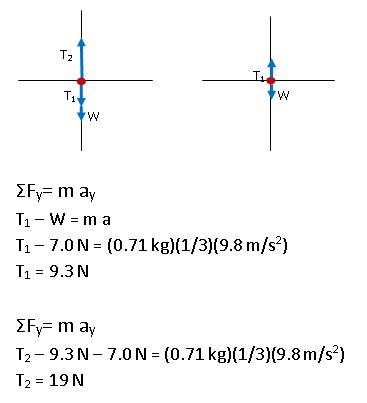
In this problem, the wires on and within the lamp need to be strong enough to support the pieces of the lamp against gravity and to provide an additional maximum upward acceleration equal to 1/3 the weight of the lamp. The values of tension make sense--they are about 1.33 the weight of the pieces that each wire must support.
Because you were asked for the strength of the wire linking the two portions of the lamp, you were not able to treat the lamp as a single system. Whether you initially broke it into two pieces or whether you first treated it as a single system, you must examine one piece of the lamp separately in order to solve for the tension required in the lower wire.
- Why isn't normal force included on the free body diagram?
- Why isn't there air resistance?
- Why isn't buoyant force included on the free body diagram?
- Why isn't acceleration included on the free body diagram?
- Is acceleration up or down?
- Can I pick the +y direction to be down?
- Why did you focus on the lamp sections and not the wires?
Why isn't normal force included on the free body diagram?
Normal force is the contact force between two surfaces. It pushes out from the surfaces and keeps them from falling into each other. In this case, the interactions between the parts of the lamp and the elevator are shown by tension. The lamp is not resting on any surface.
Why isn't there air resistance?
In this case, the air in the elevator moves up (or down) with the elevator. The lamp is not moving through the air. Any small effects as the elevator changes speed are just that-small. Any air resistance will be much smaller than other forces in the problem.
Why isn't buoyant force included on the free body diagram?
It is true that air puts a small buoyant force on the lamp. However, the size of the upward buoyant force compared to the downward force of gravity is very small. (The ratio of the two is given by the ratio of the density of air to the density of the lamp.) So to the number of significant figures included in this problem, we do not need to take buoyant force into account.
Why isn't acceleration included on the free body diagram?
The free body diagram is a stylized drawing to help you visualize the cause of acceleration, and to directly map the drawing into the left hand side (ΣF) of Newton's Second Law. Acceleration is the effect of the forces, and therefore is not included on the list of forces. It is certainly fine to include acceleration off to the side if you like.
Is acceleration up or down?
In order for the wire not to break, it needs to be at least as strong as the greatest force it must exert. If acceleration is down, the wire only needs to partially balance the gravitational force. But if acceleration is up, the wire needs to both support the lamp fully against gravity and also to accelerate it upwards. Therefore, the greatest force occurs in the case of upward acceleration. If you don't see this, wait unti you get to the solve stage and take a look at the equation at that point.
Can I pick the +y direction to be down??
Yes. In that case, W would be in the +y direction, and the tensions would be in the -y direction. Your answer will be the same in either case.
Why did you focus on the lamp sections and not the wires?
While it is true that we want to know the tension in the wires, in this case, we don't have much information about them. But we do know about the weight and motion of the lamp. Because the motion of the lamp depends on the tension in the wires, we can learn about the tensions through the motion of the lamp.