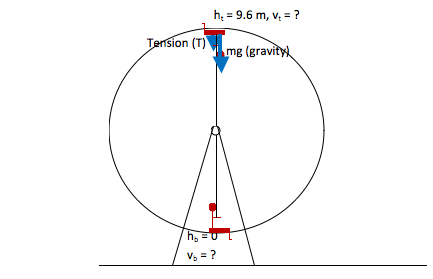
A child is playing on a tall swing set at the park. The chain on her swing is about 4.8 m long. She wants her mother to push her fast enough that she can swing over the top of the swing set in a circle (with the chains taut.) How fast must her mother push her at the bottom of the swing in order for her to follow a circular path at the top?
-
This is a two part problem. You need to look at both energy and forces in order to understand it.
It is perhaps most obvious to see the conservation of energy nature of this problem. As the swing goes around in a vertical circle, it changes speed. The swing is faster at the bottom of the motion, and gets slower as it moves to the top. As long as frictional forces are either known or small, any time you compare the speed of an object at two different locations, conservation of energy is the most direct way to understand the problem.
If you only recognized this as a conservation of energy problem, you would quickly discover that you need additional information. You can find the speed of the swing at the bottom of the circle by looking at energy only if you know the speed at the top of the circle. It cannot be zero, because if it was gravity would pull the swing straight down. So to learn the speed of the swing at the top of the circle, you are asked to relate motion (speed at the top of the circle) to force (gravity and tension). Force and motion of a single object are always related through Newton’s Second Law, so this is also a force or 2nd Law problem.
-
Can this problem be worked using kinematics?
If you recognize that speed is changing because of gravity, you can use kinematics to relate the speeds at the top and the bottom of the circle. You will still need to use Newton’s Second Law to find the speed of the swing at the top of the circle.
Isn’t vt zero?
Remember that moving in a circle means that you have an inward net force acting on the object. If the inward force is exactly the right size for the speed of the object (exactly mv2/r) then the object will follow a circular path. If the inward force is too small for the speed of the object, the object will turn but not go in a circle. If it is too large for the speed of the object, the object will move inward from the circular path. In other words, this problem asks you to relate force and motion and so is in part a 2nd Law problem.
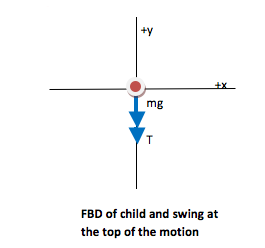
Why didn’t you draw a FBD for the swing at the bottom of the circle?
Once I use Newton’s 2nd Law to discover the speed of the swing at the top of the circle, I will use conservation of energy to find the speed at the bottom of the circle. I can’t use Newton’s 2nd Law again because I don’t know the value of tension there. Therefore, I only need a FBD for the swing at the top of the arc.
Why didn’t you pick the h = 0 to be at ground level?
You may choose h=0 to be any height that is convenient in the problem, because only the difference in height affects the amount the speed changes. The lowest point in the motion in this problem when the swing is at the bottom of the arc, and so it is easiest, but not required, to choose that point to be h=0.
Can’t you use Newton’s 2nd Law instead of Conservation of Energy for the speed of the swing at the bottom of the circle?
When an object moves in a circle, you know that the inward force must related to the motion by Fnet inward = mv2/r. So you know that you will need to approach motion at the top of the circle through Newton’s 2nd Law. You can’t use the 2nd Law at the bottom of the circle because both v and T are unknown there.
Why isn’t acceleration shown on the figure?
The free body diagram is a stylized drawing to help you visualize the cause of acceleration, and to directly map the drawing into the left hand side (ΣF) of Newton’s Second Law. Velocity gives acceleration which is the effect of the forces, and therefore is not included on the list of forces.
Remember that moving in a circle means that you have an inward net force acting on the object. If the inward force is exactly the right size for the speed of the object (exactly mv2/r) then the object will follow a circular path. If the inward force is too small for the speed of the object, the object will turn but not go in a circle. If it is too large for the speed of the object, the object will move inward from the circular path. In other words, this problem asks you to relate force and motion and so is in part a 2nd Law problem.
When an object moves in a circle, you know that the inward force must related to the motion by Fnet inward = mv2/r. So you know that you will need to approach motion at the top of the circle through Newton’s 2nd Law. You can’t use the 2nd Law at the bottom of the circle because both v and T are unknown there.
You may choose h=0 to be any height that is convenient in the problem, because only the difference in height affects the amount the speed changes. The lowest point in the motion in this problem when the swing is at the bottom of the arc, and so it is easiest, but not required, to choose that point to be h=0.
Tension is the result of the molecular attractions in the chain holding it together. Therefore, it always acts toward the center of a chain. It is a passive force—its value depends on the motion and other forces present.
-
ΣF=ma
The key equation for any problem that relates forces and motion is Newton’s Second Law. The first task in this problem is to find the speed of the swing at the top of the circle, which involves relating gravity and tension to centripetal acceleration.
KEb + PEb = KEt + PEt - Wnc
Once you know the speed of the swing at the top of the motion, you will relate it to the speed at the bottom of the motion through conservation of energy. The gravitational energy that is lost as the swing goes down in height is converted to kinetic energy. In this case, there is no work done by non-conservative forces, and so if your book does not include the Wnc term as it teaches conservation of energy, it is fine to leave it out at this stage.
Obviously, you can set up the problem in either order. However, you will have to solve ΣF=ma mathematically before you can fully solve KEb + PEb = KEt + PEt - Wnc.
-
Step 1

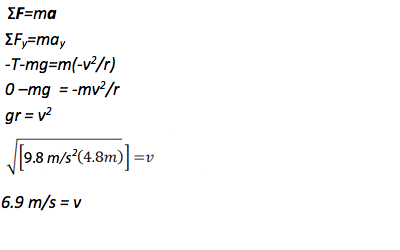
Now that you know how fast the swing must move at the top of the circle in order to stay on a circular path while gravity pulls inward, you are ready to use conservation of energy to find the speed of the swing at the bottom of the circle.
----------------------------------------------------------------------------------------------
Step 2
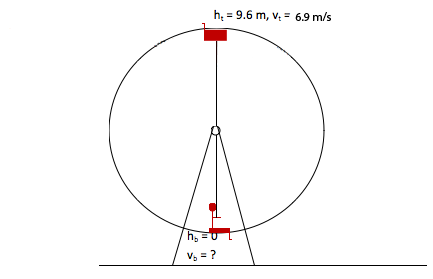
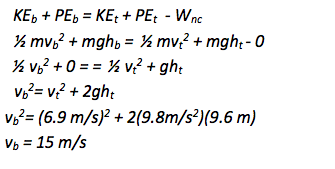
The speed of the swing at the bottom of the circle is the information that was requested in this problem. No further mathematical solution is necessary.
The chain is 4.8 m long. At the top of the motion, the swing is two chain lengths, or 9.6 m, above its position at the bottom of the motion.
Remember that moving in a circle means that you have an inward net force acting on the object. If the inward force is exactly the right size for the speed of the object (exactly mv2/r) then the object will follow a circular path. If the inward force is too small for the speed of the object, the object will turn but not go in a circle. If it is too large for the speed of the object, the object will move inward from the circular path.
Here, you have two potential inward forces when the child is at the top of the motion: gravity and tension. Tension is a passive force (its value changes depending on the motion and other forces) and so can be as small as zero. Gravity, however, is an active force with the value of mg, not zero. Therefore, in order to follow a circular path with net inward force to equal mv2/r, velocity cannot be zero and you need to use Newton’s 2nd Law to find its value.Once I use Newton’s 2nd Law to discover the speed of the swing at the top of the circle, I will use conservation of energy to find the speed at the bottom of the circle. I can’t use Newton’s 2nd Law again because I don’t know the value of tension there. Therefore, I only need a FBD for the swing at the top of the arc.
All objects near Earth experience a downward force of gravity equal to mass of the object x 9.8 m/s2. The swing cannot be stopped at the top of the circle and still follow a circular path, because gravity is always pulling downward on the swing.
In this case, the problem asked how fast the mother “must” push the child. Other words you will frequently see in physics problems are things like minimum, maximum, highest, lowest, fastest, or slowest. All of these words are asking about a limiting (or borderline case.) This problem could be rephrased to ask "what is the slowest speed that the mother could push..."
Whenever you are asked about a limiting case in a force problem, there will be a passive force (one whose value depends on the motion and other forces present) and so you need to look at the minimum or maximum value of that passive force.
In this case, you know that the faster you go around in a circle the more force you need to pull you in. So the slowest you can go is when the inward force is the least—or when tension is zero.Why is 9.8 m/s2 positive?
The force of gravity acts downward, which is the negative y-direction. Therefore, mg is given a negative sign in the equation. Do not also give 9.8 m/s2 a negative sign, or you will double count the direction.
Why is acceleration negative?
Whenever an object follows a circular path, its acceleration has a magnitude of v2/r and is directed inward. When the swing is at the top of the motion, “inward” is “down” which was chosen to be the negative y direction.
How do you know tension is zero?
In this case, the problem asked how fast the mother “must” push the child. Other words you will frequently see in physics problems are things like minimum, maximum, highest, lowest, fastest, or slowest. All of these words are asking about a limiting (or borderline case.) This problem could be rephrased to ask "what is the slowest speed that the mother could push..."
Whenever you are asked about a limiting case in a force problem, there will be a passive force (one whose value depends on the motion and other forces present) and so you need to look at the minimum or maximum value of that passive force.
In this case, you know that the faster you go around in a circle the more force you need to pull you in. So the slowest you can go is when the inward force is the least—or when tension is zero.My numbers are close but not exactly what is shown in the equation. Am I close enough?
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
The force of gravity acts downward, which is the negative y-direction. Therefore, mg is given a negative sign in the equation. Do not also give 9.8 m/s2 a negative sign, or you will double count the direction.
To get to this stage, I divided by m and multiplied by r.
r in the formula for centripetal acceleration refers to the radius of the circle and not the height of the swing.
Both tension and gravity act downward, which was chosen to be the negative direction in this coordinate system.
Why is 9.8 m/s2 positive?
It is true that the force of gravity acts downward, which is the negative y-direction. However, energy is not a vector and g refers to + 9.8 m/s2 . In other words, if h > 0, gravitational potential energy is positive.
How did you know what to fill in for potential energy?
OrDo I need to consider work done by tension in the chain?
You need to consider all conservative forces acting on the system when you compute the potential energy term. In this case, there are no springs or external electric fields, and so the only potential energy that changes as the swing moves is the potential energy due to gravity.
Also note that tension does not do any work on the system. Remember, W=Fd(cosθ). The angle between tension and direction of motion is 900, and cos(900) = 0.I don’t know the mass of the child and the swing. How can I solve the equation?
Because both gravitational potential energy and kinetic energy depend on the mass, it divides out of all terms.
My numbers are close but not exactly what is shown in the equation. Am I close enough?
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
Whenever an object follows a circular path, its acceleration has a magnitude of v2/r and is directed inward. When the swing is at the top of the motion, “inward” is “down” which was chosen to be the negative y direction.
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
Wnc is any work done by non-conservative forces, such as friction or a push, which take energy in or out of the system of interest. Some books teach you to always think about this term, others only add it if it isn’t zero. In this case, there is no significant non-conservative force and so the term is zero.
Also note that tension does not do any work on the system. Remember, W=Fd(cosθ). The angle between tension and direction of motion is 900, and cos(900) = 0.You need to consider all conservative forces acting on the system when you compute the potential energy term. In this case, there are no springs or external electric fields, and so the only potential energy that changes as the swing moves is the potential energy due to gravity.
Also note that tension does not do any work on the system. Remember, W=Fd(cosθ). The angle between tension and direction of motion is 900, and cos(900) = 0.Because both gravitational potential energy and kinetic energy depend on the mass, it divides out of all terms.
h=0 was chosen to be at the bottom of the motion in this problem. Remember, only relative heights matter and so you can pick h=0 wherever it is most convenient.
The height of the swing at the top of the circle is twice the length of the chain.
It is true that the force of gravity acts downward, which is the negative y-direction. However, energy is not a vector and g refers to + 9.8 m/s2 . In other words, if h > 0, gravitational potential energy is positive.
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
Isn’t velocity zero at the top of the circle?
This is one of the most common mistakes to make in a vertical circle problem. Remember that moving in a circle means that you have an inward net force acting on the object. If the inward force is exactly the right size for the speed of the object (exactly mv2/r) then the object will follow a circular path. If the inward force is too small for the speed of the object, the object will turn but not go in a circle. If it is too large for the speed of the object, the object will move inward from the circular path.
Here, you have two potential inward forces when the child is at the top of the motion: gravity and tension. Tension is a passive force (its value changes depending on the motion and other forces) and so can be as small as zero. Gravity, however, is an active force with the value of mg, not zero. Therefore, in order to follow a circular path with net inward force to equal mv2/r, velocity cannot be zero.
Why isn’t friction acting on the chain?
There is a small amount of friction on the swing. However, the design of a swing set is such to make the frictional force fairly small and so it can be ignored to the accuracy of this problem.
Why isn’t there air resistance?
There is! However, air resistance depends on velocity (squared) as well as on cross sectional area, and so at low speeds (such as swinging on a swing) it is much smaller than the other forces present (gravity) and can therefore be ignored for the accuracy required in this problem.
Why isn’t velocity included on the free body diagram?
The free body diagram is a stylized drawing to help you visualize the cause of acceleration, and to directly map the drawing into the left hand side (ΣF) of Newton’s Second Law. Velocity gives acceleration which is the effect of the forces, and therefore is not included on the list of forces.
Can I pick the +y direction to be down?
Yes. In that case, mg and T would be in the +y direction, as would acceleration (towards the center of the circle.) Your answer will be the same in either case.
Why isn’t normal force included on the free body diagram?
Normal force is the contact force between two surfaces. It pushes out from the surfaces and keeps them from falling into each other. In this case, the child and swing are moving together and you do not need to know the contact force between them, so it is easiest to treat them as a single system. That system does not rest on a surface; it interacts with the swing set through the tension in the chains.
Why isn’t buoyant force included on the free body diagram?
It is true that air puts a small buoyant force on the child. However, the size of the upward buoyant force compared to the downward force of gravity is very small. (The ratio of the two is given by the ratio of the density of air to the density of a person.) So to the number of significant figures included in this problem, we do not need to take buoyant force into account.
-
This problem asked you to think about the motion of the swing from both the perspectives of force and of energy.

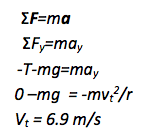
Because the swing needs to move fast enough at the top of the circle to prevent falling straight down due to the effects of gravity, the first step is to look at force and motion and to find the minimum speed of the swing at the top of the arc. Words like minimum or maximum suggest that a passive force is at one of its extreme values. In this case, the slowest speed corresponds to the smallest possible tension of zero.

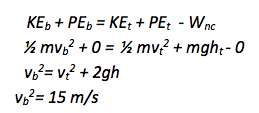
Because the gravitational energy that the swing loses as it moves downward in the circle becomes kinetic energy, we can use conservation of energy to find the speed of the swing at the bottom of the motion which would correspond to a speed of 6.9 m/s at the top.
In this case, the high speeds required for the swing (15 m/s is about 34 mph) explain why you couldn’t swing over the top of a swing set as a child no matter how hard you tried.
- Isn’t velocity zero at the top of the circle?
- Why isn’t friction acting on the chain?
- Why isn’t there air resistance?
- Why isn’t velocity included on the free body diagram?
- Can I pick the +y direction to be down?
- Why isn’t normal force included on the free body diagram?
- Why isn’t buoyant force included on the free body diagram?
