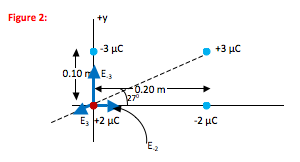
Four point charges are fixed in place as shown in the diagram.
a) What is the electric field experienced by the +2 µC charge?
b) What is the force on the +2 µC charge?
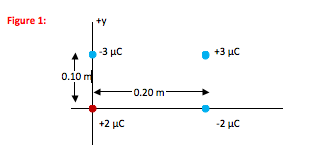
-
In this problem, you are first asked to find the electric field due to a grouping of point charges. This is a definition problem—the field is caused by the charges and you know an equation that relates them. Quantifying electric field is merely restating the charge and location information that you already have in a slightly different way. Likewise, electric force between point charges is also a definition problem for the same reasons.
Only the 2 µC charge is identified as the system of interest in this problem, because you want to know the field and force on that charge. The other charges are responsible for the interaction—they are the surroundings with which the system interacts.
This problem feels more complicated than many definition problems because the desired quantities are vectors. Therefore, you will need to do the additional math of dividing vectors into components. That math, however, does not change the overall approach to the problem.
-
Although many definition problems do not require pictures, you will want them in this case to help you with the vector addition that is required.
Part a):
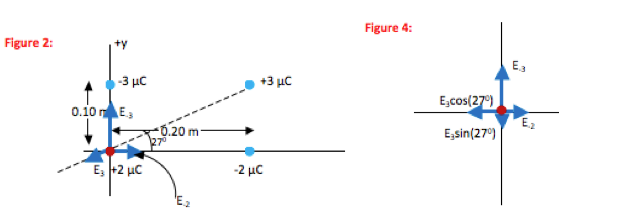
------------------------------------------------------------------------------
Part b):
-
Part a)
In equation form, electric field due to a point charge is defined as
E = (kq)/r2
In this case, you will need the vector sum of the field due to three charges.
Part b)
Once you know electric field, the most straightforward way to work part b) is to use the definition of electric force on a charge in an electric field: F = qE.
If you are using this example for a problem in which you are only asked for the force due to point charges, you should use the definition of force due to a point charge
F = (k q1 q2)/r2
and again you will need to find the vector sum of three forces.
Both methods are shown in this example. -
Step 1
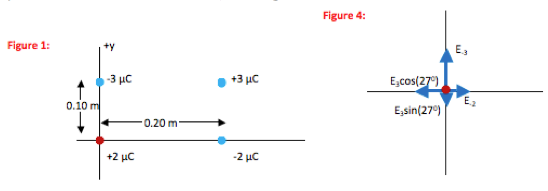
Find the electric field due to each point charge from the definition of electric field:
E-3 = (kq-3) / r2
E-3 = (9.0 x 109 N∙m2/C2)( 3 x 10-6 C) / (0.10 m)2
E-3 = 2.7 x 106 N/C
E-2 = (kq-2)/r2
E-2 = (9.0 x 109 N∙m2/C2)( 2 x 10-6 C) / (0.20 m)2
E-2 = 4.5 x 105 N/C
E3 = (kq3)/r2
E3 = (9.0 x 109 N∙m2/C2)( 3 x 10-6 C) / (0.224 m)2
E3 = 5.4 x 105 N/C
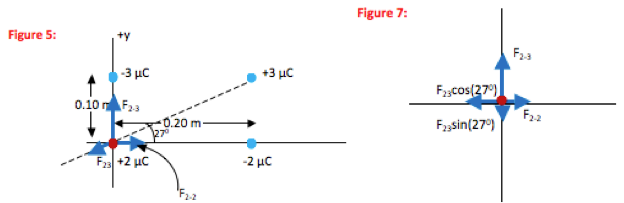
Find the x- and y-components of each field in preparation for doing the vector sum:
E3x = E3cos(27o) = -5.4 x 105 N/C cos(27o) = -4.8 x 105 N/C;
E3y = E3sin(27o) = -5.4 x 105 N/C sin(27o) = -2.5 x 105 N/C
E-3x = 0; E-3y = +2.7 x 106 N/C
E-2x = +4.5 x 105 N/C; E-2y = 0
Find the vector sum of the three fields to get the total field:
Ex = E-3x + E-2x + E3x = 0 + 4.5 x 105 N/C + (-4.8 x 105 N/C) = -3 x 104 N/C
Ey = E-3y + E-2y + E3y = 2.7 x 106 N/C + 0 + (-2.5 x 105 N/C) = 2.5 x 106 N/C
E2 = Ex2 + Ey2 = (-3 x 104 N/C)2 + (2.5 x 106 N/C)2 = 6.25 x 1012 N2/C2
E = 2.5 x 106 N/C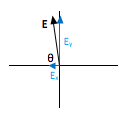
tanθ = Ey / Ex = (2.5 x 106 N/C) / (3 x 104 N/C) = 83.3
θ = 89o
The 2 µC charge experiences an electric field that has a magnitude of 2.5 x 106 N/C and is directed at an angle of 89o above the –x axis.
-----------------------------------------------------------------------------------
Step 2
If you have already solved for electric field due to the point charges, as is the case in this problem, the definition relating electric field to electric force is all you need to find force:
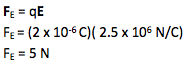
The 2 µC charge experiences an electric force that has a magnitude of 5 N and is directed at an angle of 89o above the –x axis.
If you don’t yet have the relation between force and field, you can find force beginning with the point charges.
-----------------------------------------------------------------------------------
Step 3
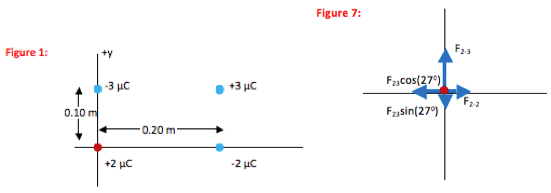
Find the electric field on the 2µC charge due to each of the other point charges from the definition of electric force:
F2-3 = (kq-3q2) / r2
F2-3 = (9.0 x 109 N∙m2/C2)( 3 x 10-6 C)(2 x 10-6 C) / (0.10 m)2
F2-3 = 5.4 N
F2-2 = (kq-2q2)/r2
F2-2 = (9.0 x 109 N∙m2/C2)( 2 x 10-6 C)(2 x 10-6 C) / (0.20 m)2
F2-2 = 0.9 N
F23 = (kq3)q2/r2
F23 = (9.0 x 109 N∙m2/C2)( 3 x 10-6 C)(2 x 10-6 C) / (0.224 m)2
F23 = 1.1 N
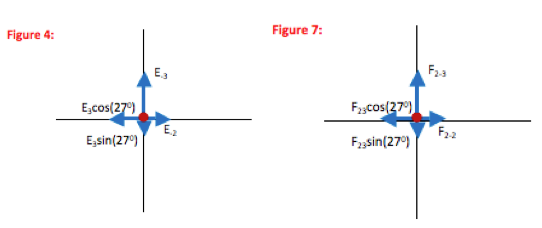
Find the x- and y-components of each field in preparation for doing the vector sum:
F23x = F23cos(27o) = -1.1 N cos(27o) = -0.96 N;
F23y = F23sin(27o) = -1.1 N sin(27o) = -0.49 N
F2-3x = 0; F2-3y = +5.4 N
F2-2x = +0.9 N; F2-2y = 0
Find the vector sum of the three fields to get the total field:
Fx = F2-3x + F2-2x + F23x = 0 + 0.9 N + (-0.06 N
Fy = F2-3y + F2-2y + F23y = 5.4 N + 0 + (-0.49 N) = 4.9 N
F2 = Fx2 + Fy2 = (-0.06 N)2 + (4.9 N)2 = 24 N2
F = 4.9 N
tanθ = Fy / Fx = (4.9 N) / (0.06 N) = 82
θ = 89o
The 2 µC charge experiences an electric force that has a magnitude of 5 N and is directed at an angle of 89o above the –x axis.
Isn’t this a Newton’s Second Law problem?
No. In Newton’s Second Law, you are asked to relate the forces on an object to the motion of that object. In this case, you aren’t asked about motion (in fact, the charges are fixed in place by non-specified forces) but rather you are just asked for the electric force and field. This is the equivalent of being asked for gravitational force when you are given masses.
How do you know the direction of electric field?
Electric field is defined as having the same direction as force on a positive charge. In other words, electric field due to a negative charge points in towards the charge, and electric field due to a positive charge points out away from the charge. So to draw the electric field at any point, sketch a guide line between that point and the charge whose field you want to draw. Then draw the field in or out along that guideline.
Why didn’t you include the field of the 2 µC charge?
An object cannot put a force on itself—it doesn’t feel its own field. So the 2 µC charge experiences a force due to (the field of) the -2 µC charge, the 3 µC charge, and the -3 µC charge, but not due to itself.
How do you know that the angle between E3 and the –y axis is 27o?
You probably learned this as “opposite angles are congruent” in geometry. When two lines intersect (in this case, the x-axis and the guideline between the origin and the 3 µC charge,) the angles opposite each other are the same.
How do you know the direction of electric force?
Electric field is defined as having the same direction as force on a positive charge. In other words, electric field due to a negative charge points in towards the charge, and electric field due to a positive charge points out away from the charge. So to draw the electric field at any point, sketch a guide line between that point and the charge whose field you want to draw. Then draw the field in or out along that guideline.
How do you know that the angle between F23 and the –y axis is 27o?
You probably learned this as “opposite angles are congruent” in geometry. When two lines intersect (in this case, the x-axis and the guideline between the origin and the 3 µC charge,) the angles opposite each other are the same.
What is a µC?
The Coulomb (C) or unit of charge is quite large. Therefore, charge is often given in smaller units. One micro-Coulomb (µC) is 10-6 C.
Why did you use positive numbers for all charges?
The definition of electric field gives the magnitude of the electric field only. Direction comes from your coordinate system and the understanding that electric field points out from negative charges and in to positive charges. Therefore, it is best to use absolute values only in the equation. If you put in the sign of the charge, it is easy to mistake that for the direction of the field.
How did you find the distance to the 3 µC charge?
The +3 µC charge is 0.224 m away from the location at which you want to know the field.
How did you get the signs on the x- and y-components of E?
Electric field is out from a positive charge. In this case, out from the 3 µC charge means that at the location of the 2 µC charge the field is down and to the left. In other words, the x- and y- components are both negative.
Can’t I do this in one step by multiplying all of the charges together in the equation?
No. For one thing, each charge is at a different distance away from the point of interest. For another, you need to take the vector sum of the fields or forces. There isn’t a correct short cut.
What is a µC?
The Coulomb (C) or unit of charge is quite large. Therefore, charge is often given in smaller units. One micro-Coulomb (µC) is 10-6 C.
Why did you use positive numbers for all charges?
The definition of electric force gives the magnitude of the electric force only. Direction comes from your coordinate system and the understanding that electric field points out from negative charges and in to positive charges. Therefore, it is best to use absolute values only in the equation. If you put in the sign of the charge, it is easy to mistake that for the direction of the force.
How did you find the distance to the 3 µC charge?
The +3 µC charge is 0.224 m away from the location at which you want to know the field.

How did you get the signs on the x- and y-components of F?
Electric field is out from a positive charge. In this case, out from the 3 µC charge means that at the location of the 2 µC charge the field is down and to the left. In other words, the x- and y- components are both negative.
Can’t I do this in one step by multiplying all of the charges together in the equation?
No. For one thing, each charge is at a different distance away from the point of interest. For another, you need to take the vector sum of the fields or forces. There isn’t a correct short cut.
The direction of electric field is defined as being radially out from a positive charge and radially in towards a negative charge.
Point charges do not experience an electric field due to their own charge. Therefore, the field on the 2 µC charge is the vector sum of three fields—those due to the -2 µC charge, the 3 µC charge, and the -3 µC charge.
Isn’t this a Newton’s Second Law problem?
No. In Newton’s Second Law, you are asked to relate the forces on an object to the motion of that object. In this case, you aren’t asked about motion (in fact, the charges are fixed in place by non-specified forces) but rather you are just asked for the electric force and field. This is the equivalent of being asked for gravitational force when you are given masses.
How do you know the direction of an electric field?
Electric field is defined as having the same direction as force on a positive charge. In other words, electric field due to a negative charge points in towards the charge, and electric field due to a positive charge points out away from the charge. So to draw the electric field at any point, sketch a guide line between that point and the charge whose field you want to draw. Then draw the field in or out along that guideline.
How do you know the direction of the force?
Like charges are repelled from each other; negative and positive charges are attracted to each other. So just draw a guide line between the charges and sketch the force along that line either towards or away from the charge of interest (in this case, the 2 µC charge.)
What is a µC?
The Coulomb (C) or unit of charge is quite large. Therefore, charge is often given in smaller units. One micro-Coulomb (µC) is 10-6 C.
Why didn’t you include the field of the 2 µC charge?
An object cannot put a force on itself—it doesn’t feel its own field. So the 2 µC charge experiences a force due to (the field of) the -2 µC charge, the 3 µC charge, and the -3 µC charge, but not due to itself.
How did you know that the angle between E3 and the –y axis is also 27o?
You probably learned this as “opposite angles are congruent” in geometry. When two lines intersect (in this case, the x-axis and the guideline between the origin and the 3 µC charge,) the angles opposite each other are the same.
Can’t I do this in one step by multiplying or adding all of the charges together into a single equation?
No. For one thing, each charge is at a different distance away from the point of interest. For another, you need to take the vector sum of the fields or forces. There isn’t a correct short cut.
Don’t I need to know gravity and the other forces on the charges in part b)?
No, you aren’t asked for the total force on the charge, you are just asked for the total electric force on the charge.
I use E-3 to refer to the electric field due to the -3 µC charge. At the origin, the direction of this field is from the origin towards the negative charge.
I use E-2 to refer to the electric field due to the -2 µC charge. At the origin, the direction of this field is from the origin towards the negative charge.
I use E3 to refer to the electric field due to the +3 µC charge. At the origin, the direction of this field is from the origin away from the positive charge.
The dotted line is merely a guide to correctly show the direction of E3.
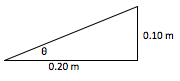
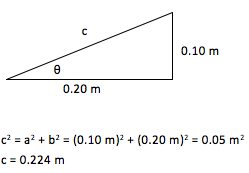
tan θ = (opposite side)/(adjacent side) = (0.10)/(0.20) = 0.50
θ = tan-1 (0.50) [or inv tan (0.50) depending on your calculator] = 270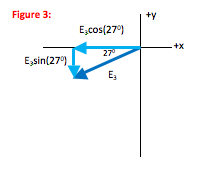
As you can see in the figure, the x- and y-components of a vector make up the sides of a right triangle. The vector itself forms the hypotenuse (h). The side of the triangle opposite the angle that you use is given by h sinθ and the side that touches the angle you use is given by h cosθ (soh cah toa)
In this case, the x-component is adjacent to the 270angle, and so is given by E3cos(270). Likewise, the y-component is opposite to the 270angle and is therefore given by E3sin(270).
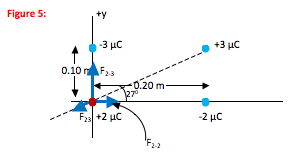
You know this angle is 270 because when two lines intersect (in this case, the x-axis and the guideline between the origin and the 3 µC charge,) the angles opposite to each other are the same.Point charges do not experience an electric force due to their own charge. Therefore, the force on the 2 µC charge is the vector sum of three forces—those due to interactions with the -2 µC charge, the 3 µC charge, and the -3 µC charge.
The direction of electric force is determined by the location of the charges and whether it is attractive (interaction between a + and a – charge) or repulsive (interaction of like charges.)I use F2-3 to refer to the electric force between the 2 µC charge and the -3 µC charge. This interaction is attractive and on a line between the two charges.
I use F2-3 to refer to the electric force between the 2 µC charge and the +3 µC charge. This interaction is repulsive and on a line between the two charges.
I use F2-2 to refer to the electric force between the + 2 µC charge and the -2 µC charge. This interaction is attractive and on a line between the two charges.
The dotted line is merely a guide to correctly show the direction of F2-3.

tan θ = (opposite side)/(adjacent side) = (0.10)/(0.20) = 0.50 θ = tan-1 (0.50) [or inv tan (0.50 depending on your calculator) = 270
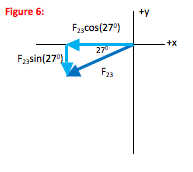
As you can see in the figure, the x- and y-components of a vector make up the sides of a right triangle. The vector itself forms the hypotenuse (h). The side of the triangle opposite the angle that you use is given by h sinθ and the side that touches the angle you use is given by h cosθ (soh cah toa)
In this case, the x-component is adjacent to the 270angle, and so is given by F23cos(270). Likewise, the y-component is opposite to the 270angle and is therefore given by F23sin(270).
You know this angle is 270 because when two lines intersect (in this case, the x-axis and the guideline between the origin and the 3 µC charge,) the angles opposite to each other are the same.k = 9.0 x 109 N∙m2/C2
Some books use 1/(4πε0) instead of k. In either case, the value is the same.The definition of electric field gives the magnitude of the electric field only. Direction comes from your coordinate system and the understanding that electric field points out from negative charges and in to positive charges. Therefore, it is best to use absolute values only in the equation. If you put in the sign of the charge, it is easy to mistake that for the direction of the field.
The -3 µC charge is 0.10 m away from the location at which you want to know the field.
The -2 µC charge is 0.20 m away from the location at which you want to know the field.
The +3 µC charge is 0.224 m away from the location at which you want to know the field.

The -3 µC charge is 0.10 m away from the location at which you want to know the force.
The -2 µC charge is 0.20 m away from the location at which you want to know the force.
The +3 µC charge is 0.224 m away from the location at which you want to know the force.

Electric field is out from a positive charge. In this case, out from the 3 µC charge means that at the location of the 2 µC charge the field is down and to the left. In other words, the x- and y- components are both negative.
Electric field acts in to a negative charge. In this case, in to the -3 µC charge means that at the location of the 2 µC charge the field is straight up. In other words, there is no x-component and the y-component is positive.
Electric force is attractive between positive and negative charges. In this case, the attraction to the -2 µC charge pulls the 2 µC charge to the right. In other words, there is no y-component to this force and the x-component is positive.”
E2 = Ex2 + Ey2 is the Pythagorean Theorem applied to the electric field vector.
For the angle shown in the figure, the y-component of electric field is opposite the angle and the x-component is adjacent.
The definition of electric force gives the magnitude of the force only. Direction comes from your coordinate system and the understanding that electric force is attractive between + and – charges and repulsive between same charges. Therefore, it is best to use absolute values only in the equation. If you put in the sign of the charge, it is easy to mistake that for the direction of the force.
Electric force is repulsive between like charges. In this case, “repelled from the 3 µC charge” means that at the 2 µC charge is pushed down and to the left. In other words, the x- and y- components of force are both negative.
Electric force is attractive between positive and negative charges. In this case, the attraction to the -3 µC charge pulls the 2 µC charge the field straight up. In other words, there is no x-component to this force and and the y-component is positive.
F2 = Fx2 + Fy2 is the Pythagorean Theorem applied to the electric force vector.
Electric field acts in to a negative charge. In this case, in to the -2 µC charge means that at the location of the 2 µC charge the field is straight to the right. In other words, there is no y-component and the x-component is positive.
For the angle shown in the figure, the y-component of electric force is opposite the angle and the x-component is adjacent.
-
The key to understanding this problem is that both parts are merely definition problems. It feels much more complicated (and takes much more work) because the quantities defined are vector quantities, and you are asked to find the sum of several individual fields (or forces.) Note that almost all of the mathematical effort in this problem is in finding the vector sum. If you don’t remember how to work with vectors and need more of a refresher than is provided in this problem, click here for an example of dividing vectors into components and click here for an example working with the result.
The definition FE = (k q1 q2)/r2 is analogous to Fg = (k m1 m2)/r2. Whenever you are given a distribution of point charges, you can find the force on one of those charges by
- using the definition to find the magnitude of each force;
- finding the x- and y-components of each force;
- adding the forces together separately in each direction.
Electric field (E) is analogous to gravitational field (g). If you know the electric field, you can find the force on any object with a charge q in that field just by the definition FE = qE (analogous to Fg = mg.)
You can also calculate electric field directly from point charges. (If you want to see where the equation comes from, just look at the color coding in the equations above. Remember, red represents the system you care about and blue represents the effect of the surroundings. So electric field contains all information about the surrounding point charges that act on your system.) Whenever you are given a distribution of point charges, you can find the electric field of those charges by
- using the definition to find the magnitude of each electric field;
- finding the x- and y-components of each electric field;
- adding the fields together separately in each direction.
- Isn’t this a Newton’s Second Law problem?
- How do you know the direction of an electric field?
- How do you know the direction of the force?
- What is a µC?
- Why didn’t you include the field of the 2 µC charge?
- How did you know that the angle between E3 and the –y axis is also 27o?
- Can’t I do this in one step by multiplying or adding all of the charges together into a single equation?
- Don’t I need to know gravity and the other forces on the charges in part b)?
