Rank the brightness of the identical light bulbs in the circuit below.
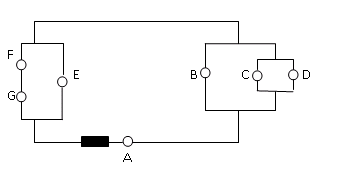
-
The brightness of a lightbulb is given by its power. P = I2R, and so brightness depends on current and resistance. If the bulbs are identical, they have the same resistance. They may not, however, experience the same current. Therefore, when you are asked to rank the brightness of identical bulbs, you are really being asked to rank the amount of current through each. This, then, is a circuit problem even though you do not need to specify the values of the currents.
Power is a measure of the amount of energy converted per time. In this case, the electric energy of the circuit is converted to light and heat energies in the light bulbs.
At a junction in a circuit, some of the current goes through one branch and some through the other(s). In other words, the current splits and therefore is not the same throughout.
Don't I need numbers to work this problem?
No. Even though you cannot give values for the current without knowing the size of the battery and the resistance of the bulbs, you can still talk about the current through each segment as a portion of the total current through the battery.
-
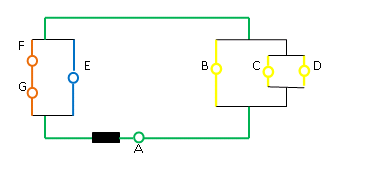
Because you do not need to solve this circuit mathematically, you do not need to reduce it to a single equivalent resistance. You do, however, need to track current. Using color to show portions of the circuit with the same current gives a very helpful visual.
How did you know all three of the "yellow" branches have the same current? Doesn't the current divide and then divide again?
Yes. If you need to go through two steps to see that all three legs have the same current, that is fine. In that case (see the "Solve" page for more elaboration) you would find that twice as much current goes through the right branch (two resistors in parallel) as through the single resistor of the left branch, because resistance is less when resistors are connected in parallel. That larger current then splits equally when it comes to the second junction.
Current is not used up in resistors. Electric energy is converted to other forms (in this case heat and light) but the current remains the same. Therefore, any portion of the circuit where there is a single path must have the same current, even if the electrons go through a resistor before they get to that portion of the path.
At this portion of the circuit, the current has a choice--it splits across all three paths. Therefore, the current in each path is not the same as the green current. Because the resistance of each path is the same, the current through each path will also be the same. If you do not see that yet and gave each path its own color, that is fine. You will explore this more in the "Solve" step of the problem.
At this portion of the circuit, the current has a choice--it splits across the two paths. Because the resistance is different in the two paths, you expect the current in each to be different as well. Therefore, the two branches are given different colors to show that they have different currents.
-
There are two ideas (charge is conserved, energy is conserved) and three equations that help you understand circuits.
As applied to circuits,
Conservation of Charge gives: Current is the same through resistors in series.
Conservation of Energy gives: Voltage drop is the same across each leg of a parallel circuit.
The three equations are
Req = ΣiRi Conceptually, this means that as more resistors are added in series the resistance of the circuit element increases.
1/R
= Σi1/Ri Conceptually, this means that as more resistors are added in parallel the resistance of the circuit element decreases.
ΔV = IR Conceptually, this means that there is a "trade" between current and resistance in order to give the same voltage drop.
Because you are not asked for numbers, you only need to use the conceptual understandings behind these equations. If you think better mathematically, it is fine to use numbers to first see the relationships. Just make sure you then use that insight to understand the problem conceptually as well.
When the circuit reaches its steady state, the amount of energy (per charge) that the current gains as it goes across the battery is equal to the amount of energy (per charge) that it converts to other forms in the resistors. This balance is what determines how much current is generated by the battery. This understanding can be restated as "voltage drop is the same across each leg of a parallel circuit" because voltage is a measure of energy per charge. Regardless of which path the current takes, it must convert the same amount of energy (per charge) to other forms.
Remember, energy is converted in resistors but electrons are not used up.
You can have the same voltage drop with a small current and large resistance or with a large current and small resistance. What is more, these changes are proportional. If you compare two branches with R and 2R, there is will 2 times as much current in the R branch as in the 2R branch.
-

Because all of the current passes through the green portions of the circuit, we know that Bulb A has the greatest amount of current and is therefore the brightest.
Each leg of the yellow portion of the circuit has the same resistance. In other words, a current element will flow through Bulb B or Bulb C or Bulb D, and, because the resistances are the same, the amount of current through each is the same. Therefore, Bulbs B, C, and D have the same current and, consequently, the same brightness. Furthermore, because the green current splits into three equal parts, the yellow current is 1/3 the value of the green current.
The current does not split evenly at this junction. Bulbs F and G are in series, and so the resistance of the orange leg is twice that of the blue leg. As a result, twice as much current goes through Bulb E as through Bulb F or G. Because the blue and orange currents add to the green current, the blue current is 2/3 the value of the green current, and the orange current is 1/3 the value of the green current.
Putting this together, A is the brightest bulb, followed by E. Bulbs B, C, D F and G are all the same brightness (and the faintest.)
Even though energy is transformed, electrons are not used up. When current splits and reunites, it has the same value before and after.
Voltage drop (IR) is the same across parallel branches. If R is the same, I must also be the same.
Voltage drop (IR) is the same across parallel branches. If R is different, I must also be different by the same factor. They are inversely related.
Resistors in series add. R + R = 2R
Blue current + Orange current = Green current.
Blue current = 2 (Orange current)
2 Orange current + Orange current = Green current
3 Orange current = Green current
Green current = I; Blue current = 2/3 I; Orange and Yellow currents = 1/3 I.
-

In this problem, you are asked to understand current flow in a circuit conceptually. You know that the current out through the battery splits and recombines at junctions and electrons are not used up. Furthermore, you know that current does not split evenly at a junction. Rather, more current passes through branches that have less resistance and IR always has the same value for branches in the same parallel elemenet.
This understanding is all that is required in order to determine what fraction of the current from the battery goes through each branch of a circuit. Note that you can also use these conceptual ideas to solve circuits mathematically. If you break down the circuit into its equivalent resistance (go to the Draw page of Circuit II) and use that to find the total current (the green current in this case), you can find the other currents based on their fraction of the green current.
The light bulbs are identical. Doesn't that mean they all have the same brightness?
No. The brightness of a lightbulb is given by its power. P = I2R, and so brightness depends on current and resistance. If the bulbs are identical, they have the same resistance. They may not, however, experience the same current. Therefore, when you are asked to rank the brightness of identical bulbs, you are really being asked to rank the amount of current through each.
How would I work this problem mathematically?
This is exactly the same circuit as in Circuit II. Click here to go to Circuit II and work it mathematically. To really understand the process well, take a look at both the conceptual and mathematical solutions and see that they are the same.
