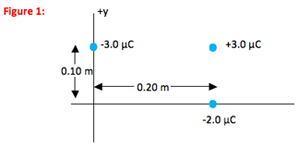
Three point charges are fixed in place as shown in the diagram.
What is the electric potential (due to these charges) at the origin?
-
In this problem, you are asked to find the electric potential due to a grouping of point charges. This is a definition problem—the electric potential is due the charges and you know an equation that relates them. Quantifying electric potential is merely restating the charge and location information that you already have in a slightly different way.
-
Although many definition problems do not require pictures, you will want one in this case to help you visualize the correct distance to each charge
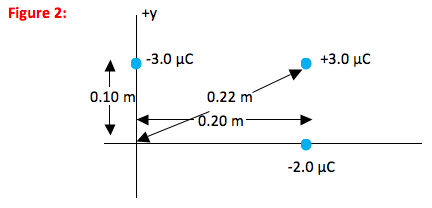
Electric potential depends on charges and on the distances between the charges and the point of interest. In this case, you want to know the electric potential at the origin and so it is useful for your picture to show the distance between each charge and the origin.
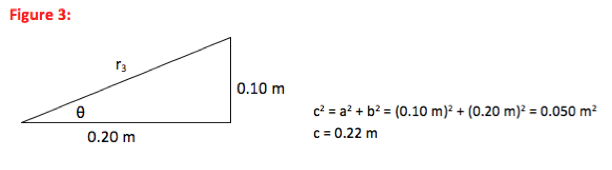
-

In equation form, electric potential due to a point charge is defined as
V = kq/r
In this case, you will need to find the sum of the potentials due to three charges. -
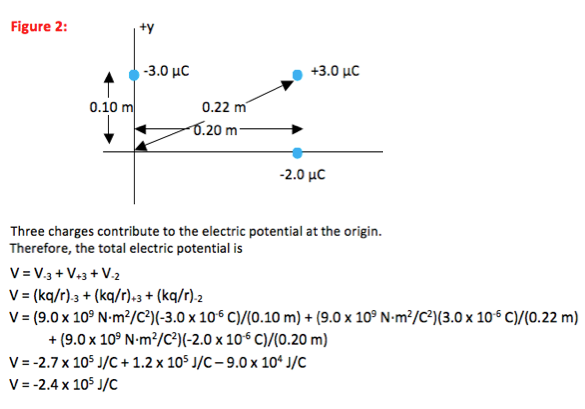
The electric potential at the origin due to the point charges shown is -2.4 X 105 J/C. No further numerical solution is required.
Isn’t this an energy problem?
No. It is true that electric potential is related to energy just as height is related to energy. However, you are not asked to examine what happens to a system as it undergoes a transformation in energy. You are just asked for electric potential and given two closely related bits of information (charge and position.)
How do you know the distance to the 3 µC charge?

What is a µC?
The Coulomb (C) or unit of charge is quite large. Therefore, charge is often given in smaller units. One micro-Coulomb (µC) is 10-6 C.
Why did you use put in signs for the charges?
1 µC = 10-6 C.
Electric potential due to a positive charge is positive, and electric potential due to a negative charge is negative. In other words, even though electric potential is a scalar, the sign of potential has meaning. (This should be familiar from other scalars like height and temperature.) You need to include the correct sign of the charge in the electric potential equation.How did you know the units for electric potential?
(N∙m2/C2)(C)/m = (N∙m)/C = J/C
This unit makes physical sense—the potential energy of a charge in a region of electric potential is equal to charge x potential, so the units of potential energy are Joules as expected.How did you find the distance to the 3 µC charge?
The +3 µC charge is 0.22 m away from the location at which you want to know the field.
Can’t I do this in one step by multiplying all of the charges together in the equation?
No. Each charge is at a different distance away from the point of interest. The total electric potential is the sum of the electric potentials due to each charge, and those terms all involve different distances.
Isn’t this an energy problem?
No. It is true that electric potential is related to energy just as height is related to energy. However, you are not asked to examine what happens to a system as it undergoes a transformation in energy. You are just asked for electric potential and given two closely related bits of information (charge and position.)
What is the difference between electric potential and electric potential energy?
Electric potential energy depends on both electric potential and the charge of an object experiencing that potential. In exactly the same way, gravitational potential energy depends on both the height of an object and the mass of that object. In other words, potential energy comes from the interaction of a system with its surroundings. Potential summarizes the conditions of the surroundings (the amount and location of the charges or masses) and potential energy includes the relevant property of the system as well as the surroundings.
What is the difference between electric potential and voltage?
The two terms are often used interchangeably. Some text books have begun to use “voltage” in order to avoid confusion between the terms “electric potential” and “electric potential energy” which name different things.
What is a µC?
The Coulomb (C) or unit of charge is quite large. Therefore, charge is often given in smaller units. One micro-Coulomb (µC) is 10-6 C.
How do you know where electric potential is zero?
Just as for gravity, it is only the value of the change in potential that will have physical significance. And so you can choose the zero point of potential just as you can choose the zero point of height. That said, there are two common conventions for the zero point of electric potential. If you are working with circuits, the electric potential of the Earth (“ground”) is taken to be zero. If you are working with point charges, the electric potential an infinite distance away from the charges is taken to be zero. That zero point (V = 0 when r = infinity) is built into the equation V = kq/r.
Can’t I do this in one step by multiplying or adding all of the charges together into a single equation?
No. Each charge is at a different distance away from the point of interest. The total electric potential is the sum of the electric potentials due to each charge, and those terms all involve different distances.
k = 9.0 x 109 N∙m2/C2
Some books use 1/(4πε0) instead of k. In either case, the value is the same.I subscripted each electric potential term with the charge associated with that term in order to keep them all straight. V-3, for example, is the electric potential due to the -3 µC charge.
k = 9.0 x 109 N∙m2/C2
Some books use 1/(4πε0) instead of k. In either case, the value is the same.The -3 µC charge is 0.10 m away from the location at which you want to know the field.
The -2 µC charge is 0.20 m away from the location at which you want to know the field.
The +3 µC charge is 0.22 m away from the location at which you want to know the field.
1 µC = 10-6 C.
Electric potential due to a positive charge is positive, and electric potential due to a negative charge is negative. In other words, even though electric potential is a scalar, the sign of potential has meaning. (This should be familiar from other scalars like height and temperature.) You need to include the correct sign of the charge in the electric potential equation.(N∙m2/C2)(C)/m = (N∙m)/C = J/C
This unit makes physical sense—the potential energy of a charge in a region of electric potential is equal to charge x potential, so the units of potential energy are Joules as expected.Only two significant figures were given in the statement of the problem, so only two significant figures were kept in the answer.
-

- Isn’t this an energy problem?
- What is the difference between electric potential and electric potential energy?
- What is the difference between electric potential and voltage?
- What is a µC?
- How do you know where electric potential is zero?
- Can’t I do this in one step by multiplying or adding all of the charges together into a single equation?
