In a cathode ray tube, electrons are "boiled" off of a filament and accelerated through a potential difference. They then strike a fluorescent screen and so can produce non-permanent images. Cathode ray tubes are used, for example, in televisions and computer monitors. Suppose you want to build a cathode ray tube that will accelerate electrons to a speed of 7.5 x 107m/s. How great a potential difference do you need? Should the potential be higher at the filament or the screen?
-
In this problem, you are asked to find the change in electric potential of an electron given a specified change in its speed. Electric potential is a measure of electric potential energy, just as height is a measure of gravitational potential energy. This is a Conservation of Energy problem.
If non-conservative forces are either known or small and if energy is converted from one form to another between the locations, then any time you compare speed of an object at two different points, conservation of energy is the most direct way to understand the problem.
In this case, you start out with stored energy due to the location of the electron in an electric potential and convert it to kinetic energy.
-
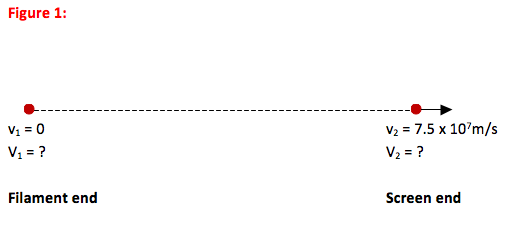
You could have found this example either on the Electricity and Magnetism page or on the Energy and Momentum page. If you found it by the later search, good for you! You have a good understanding of the interaction important to consider in this problem.
This may sound like a force or kinematics problem because of the word “accelerated.” However, you are told that the electron is accelerated to a certain speed, and so the information that you are given is actually about speed. It is equivalent to think of the acceleration as being caused by a force or due to a transformation of energy. In this case, you are asked about electric potential, which is directly related to energy.
-
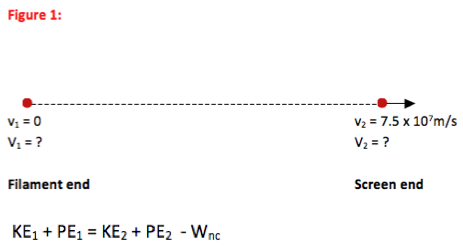
Any time you understand the motion of an object by looking at its energy, you begin with the Conservation of Energy equation.
-

The electron needs to be accelerated through a potential difference of 16 J/C. The electric potential is higher at Point 2 - the screen.
Can this problem be worked using kinematics?
No. You don’t have enough information about the distance over which the electrons travel (or the time it takes) to be able to calculate acceleration (and therefore force and, ultimately, electric potential.)
Can this problem be worked using dynamics?
No. You are told that the electrons are accelerated to a certain speed, and so the information that you are given is actually about speed. It is equivalent to think of the acceleration as being caused either by a force or due to a transformation of energy. In this case, you are asked about electric potential, which is directly related to energy.
How do you know v1 = 0?
The filament is heated up until the electrons have enough energy to be freed. At this lowest energy, they don’t have much additional kinetic energy. Even if they have some speed, it will be significantly less than 7.5 x 107m/s and so won’t show up to the accuracy of this problem.
Why don’t you include gravitational potential energy?
Over the short distance of a TV or computer monitor and given the high speeds at which electrons travel, any deviation from horizontal is insignificant.
Both electric potentials are unknown. Can this problem be solved?
You know that the electric potential changes as the electron goes from the filament to the screen. You are only asked for the value of that difference, and so you don’t need to know the actual value of electric potential at either point. You will solve for V2-V1.
This is not the way my book writes the Conservation of Energy equation. What is “Wnc”?
Wnc is any work done by non-conservative forces, such as friction or a push, which take energy in or out of the system of interest. Some books teach you to always think about this term, others only add it if it isn’t zero. Still others may write it as KE1 + PE1 + Eadded to the system = KE2 + PE2 + Eleaving the system. If there is no significant non-conservative force (as is the case in this problem) then all three versions of the equation are equivalent. Including Wnc in some form is more general and gives an equation that is true in all situations, including those with non-conservative forces.
Why don’t you include gravitational potential energy?
Over the short distance of a TV or computer monitor and given the high speeds at which electrons travel, any deviation from horizontal is insignificant.
How did you know the values for q and m?
You can look up properties of the electron in your text or on line.
How do you know v1 = 0?
The filament is heated up until the electrons have enough energy to be freed. At this lowest energy, they don’t have much additional kinetic energy. Even if they have some speed, it will be significantly less than 7.5 x 107m/s and so won’t show up to the accuracy of this problem.
Why don’t you include gravitational potential energy?
Over the short distance of a TV or computer monitor and given the high speeds at which electrons travel, any deviation from horizontal is insignificant.
Can this problem be worked using kinematics?
No. You don’t have enough information about the distance over which the electrons travel (or the time it takes) to be able to calculate acceleration (and therefore force and, ultimately, electric potential.)
Can this problem be worked using dynamics? We are told about acceleration.
No. You are told that the electrons are accelerated to a certain speed, and so the information that you are given is actually about speed. It is equivalent to think of the acceleration as being caused either by a force or due to a transformation of energy. In this case, you are asked about electric potential, which is directly related to energy.
Do you need to take relativistic effects into account?
No. Even at 7.5 x 107m/s, γ = 1.03, or 1.0 to the accuracy of this problem.
The filament is heated up until the electrons have enough energy to be freed. At this lowest energy, they don’t have much additional kinetic energy. Even if they have some speed, it will be significantly less than 7.5 x 107m/s and so won’t show up to the accuracy of this problem.
You know that the electric potential changes as the electron goes from the filament to the screen. You are only asked for the value of that difference, and so you don’t need to know the actual value of electric potential at either point. You will solve for V2-V1.
In this problem, you want to examine the change in energy of the electron between the filament and the screen. You know speed of the electron at the screen is 7.5 x 107 m/s.
Some books use PE for potential energy. Others use P.E. and others use U. All are equivalent and refer to the same thing.
Wnc is any work done by non-conservative forces, such as friction or a push, which take energy in or out of the system of interest. Some books teach you to always think about this term, others only add it if it isn’t zero. Still others may write it as KE1 + PE1 + Eadded to the system = KE2 + PE2 + Eleaving the system. If there is no significant non-conservative force (as is the case in this problem) then all three versions of the equation are equivalent. Including Wnc in some form is more general and gives an equation that is true in all situations, including those with non-conservative forces.
There are no significant non-conservative forces (like friction) present in this problem, and so the work done by non-conservative forces is about zero.
The only potential energy that undergoes a change in this problem is electric potential energy, which is given by the definition PEE = qV. No other potential energies need to be considered because they contribute equally to both sides of the equation and so subtract out.
Subtract qV2 from both sides of the equation, and factor out the q from both potential energy terms.
You can look up properties of the electron in your text or online.
1 kg (m/s)2/C = 1 (kg m2/s2)/C = 1 J/C
The values for point 1 can be put into the equation directly from your picture.
The values for point 2 can be put into the equation directly from your picture.
Although electric potential is higher at the ending point, electric potential energy is lower. PEE = qV and q is negative for an electron. So a higher V gives a more negative, or lower, PE. This makes sense—initial PE is converted to KE as the electron moves to the screen.
-

In this problem, you are asked to find the potential difference required to accelerate an electron from rest to 7.5 x 107m/s. The energy conversion chain for this motion is
electric potential energy→kinetic energy
as reflected in the second line of the equation above.
You should notice that although electric potential is higher at the ending point, electric potential energy is lower. PEE = qV and q is negative for an electron. So a higher V gives a more negative, or lower, PE. This makes sense—initial PE is converted to KE as the electron moves to the screen.
