A 4.2 cm long solenoid is wrapped with 1000 loops of wire. What is the magnetic field down the center of the solenoid if a current of
0.66 A is run through the wire as shown?
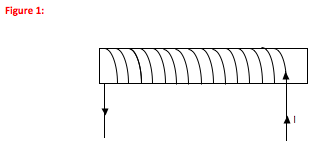
-
In this problem, you are given the current in a solenoid and asked for the magnetic field due to that current. This is just a definition problem.
-
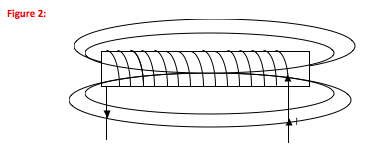
There is no need for a picture in most definition problems. However, magnetic fields are three dimensional and so it is helpful to use a picture to visualize the field and the current that causes it. In addition, when you use partially-solved equations (such as the definition of the magnetic field due to a solenoid) you also must use what you know about the shape of the field. For a tightly-wrapped solenoid, we know the field is essentially uniform down the center axis inside the solenoid, and wraps like the field of a bar magnet outside. This information will not come from the equation.
-
In equation form, the magnitude of the magnetic field inside a solenoid is
B = µ0 n I
The direction of the magnetic field is given by the two step right hand rule:
1.) Point your thumb in the direction of either I or B, whichever is straight.
2.) The direction your fingers curl gives the direction of the remaining vector (either I or B.)
or
“Thumb straight, fingers curl.”
-

B = µ0 n I
B = (4π x 10-7 T∙m/A)(1000/0.042 m)(0.66 A)
B = 0.020 T
To find the direction of magnetic field down the center of the solenoid, use your knowledge of the shape of the field. In this case, the current wraps around the core of the solenoid, so it goes with your fingers. The magnetic field is straight down the inside, so it goes with your thumb. (Thumb straight, fingers curl.)
Current wraps up in front and down in back of the solenoid as shown—place your right hand so that the fingers point up when they are in front of the picture and down as they bend to the back (the easiest way to see this is to hold your pencil as if it is the solenoid and wrap your fingers to be the current.) To do this, your thumb points to the left.
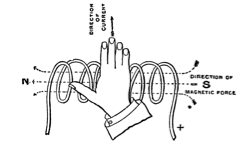
Source of image: Florida Center for Instructional Technology, http://etc.usf.edu/clipart/
There is a 0.020 T magnetic field to the left in the inside of the solenoid.
-
B = µ0 n I
B = (4π x 10-7 T∙m/A)(1000/0.042 m)(0.66 A)
B = 0.020 T
This problem is merely a definition problem—you are asked to calculate the magnetic field from the current that causes it. Because the general relationship between current and magnetic field is complicated, in most courses you are given several partially-solved special case equations. In this case, you need to use the equation as solved for a solenoid.
You also need to use what you know about the shape of the magnetic field in a solenoid. The two step right hand rule allows you to determine which direction the field points, but does not tell you the shape of the field.
Why do you call this a definition problem rather than a force problem?
It is true that magnetic field is related to magnetic force. However, in this problem you are not asked to relate that force to the motion of a charge in the field. Instead, you are asked to compute the field from the current causing it. This is analogous to being asked for frictional force if you are given µ and normal force.
How did you know which right hand rule to use?
The equation for magnetic field relates two vectors—current and magnetic field. Therefore, you want the two step right hand rule.
It relates
1) the direction of magnetic field
to
2) the direction of the current that causes it.
The equation for magnetic field relates two vectors—current and magnetic field. Therefore, you want the two step right hand rule.
It relates
1) the direction of magnetic field
to
2) the direction of the current that causes it.
You can look up the value of µ0 in your text book.
(4.2 cm)/(100 cm/m) = 0.042 m
The arrows on the figure show that the current flows up the wire on the front side of the solenoid and goes down on the back side.
Current flows from the + side of the battery (on the right) to the negative side. Therefore, it flows up along the right side of the wire, back down around the back of the loop, up again in front, etc.
In this equation, n refers to the number of turns per length, and not just to the number of turns.
Why do you call this a definition problem rather than a force problem?
It is true that magnetic field is related to magnetic force. However, in this problem you are not asked to relate that force to the motion of a charge in the field. Instead, you are asked to compute the field from the current causing it. This is analogous to being asked for frictional force if you are given µ and normal force.
