An electron is traveling to the right with a speed of 8.5 x 106 m/s when a magnetic field is turned on. The strength of the magnetic field is 0.050 T, and it is directed into the paper. Describe the path of the electron after the field has been turned on. (You may ignore relativistic effects.)
-
In this problem, you are asked to relate motion (the path of the electron) to force (magnetic field is directly related to magnetic force, just as g is directly related to gravitational force). Force and motion of a single object are always related through Newton’s Second Law, so this is a force or 2nd Law problem.
-
Step 1:
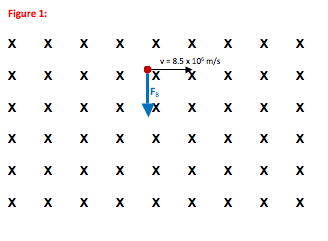
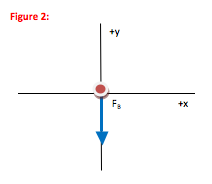
In order to determine the direction of magnetic force on an electric charge moving in a i, we need to use the 3-step right hand rule. (Force, velocity and field are all vectors—the 3-step right hand rule relates the direction of these three vectors.)
Although you now have a free body diagram, you also need to recognize that magnetic force is always perpendicular to the motion of the charge. So when the charge changes direction, the force also changes direction. Continue to step 2 to explore the implications of the changing direction of force on the path of the electron.
--------------------------------------------------------------------------------------------
Step 2:

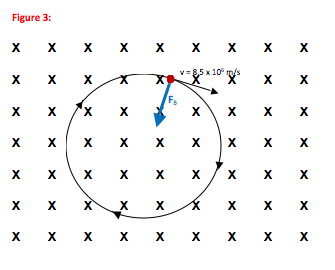
As the magnetic force acts on the electron, the electron changes direction. Using the right hand rule again shows that force also changes direction. In other words, the magnetic force continues to point perpendicular to velocity and pulls the electron in a clockwise circle.
To fully describe the path of the electron, you now need to find the size of that circle.
-
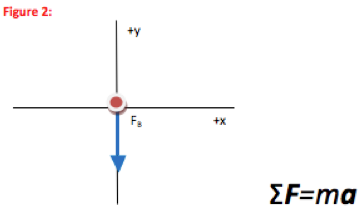
The key equation for any problem that relates forces and motion is Newton’s Second Law. Regardless of what quantity you are asked to find, begin with the Second Law. If additional information is needed, it will become apparent as you proceed.
-

The magnetic field causes the electron to move clockwise in a circle with a radius of 9.7 x 10-7 m. Nothing further is needed to describe the path of the electron.
-

In this problem, you are asked to describe the path of a moving charge when you are given information related to the force on that charge. It is a Newton’s 2nd Law problem.
This is a case where experience helps make the problem easier: any motion of a charge that is perpendicular to a magnetic field gives rise to circular motion of that charge. This is worth noting and remembering for future problems. To describe the path of the charge, then, you merely need to determine the size of the circle and which direction (clockwise or counter-clockwise) the charge moves around it.
Although you might initially be surprised at how small the circle is, note that the tiny mass of the electron means that you get a huge acceleration for even a small force.
Why did you draw the magnetic field as X’s?
Magnetic force is always perpendicular to both the motion of electric charges and the direction of the magnetic field. This means that magnetic force problems are inherently three-dimensional. The convention for drawing three dimensions on a two-dimensional piece of paper is that an “X” represents a vector into the plane of the paper and a “ ∙ ” represents a vector directed out of the paper.
Why did you draw the velocity of the electron on the figure?
Although you typically don’t sketch velocity on a drawing that prepares you to make a Free Body Diagram, you do need to track velocity here in order to use the right hand rule. In other words, the direction of force depends on the direction of velocity, and so velocity plays an important role in drawing the free body diagram. Note that while velocity is sketched on the initial figure, it is not included on the FBD itself.
How do you use the 3-step right hand rule?
In the 3-step right hand rule, your thumb gives the direction of the force on a positive charge, your index finger points with the motion of the charge, and your palm (or bent remaining three fingers) point in the direction of the magnetic field. So in this case, point your palm or bent fingers into the paper while your index finger points to the right. In this orientation, your thumb points up toward the top of the paper so the force on a + charge is up. The force on a – charge is the reverse, or down.
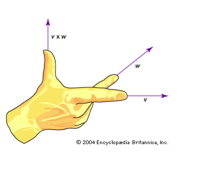
Source of image: Encyclopedia Britannica Inc., http://www.britannica.com/
How do you know the electron moves in a circle?
Magnetic force depends on sine of the angle between magnetic field and velocity. (For those of you in a calculus based class, magnetic force is the cross product of magnetic field and velocity.)
In other words, any component of velocity that is parallel to the magnetic field gives no contribution to magnetic force (a charge moving parallel to the field will continue at constant velocity) and any component of velocity that is perpendicular to magnetic field results in a force perpendicular to velocity and causes the charge to move in a circle.
In this problem, the electron’s velocity is entirely perpendicular to the magnetic field.
FB = qvB sinθ
Although you typically don’t sketch velocity on a drawing that prepares you to make a Free Body Diagram, you do need to track velocity here in order to use the right hand rule. In other words, the direction of force depends on the direction of velocity, and so velocity plays an important role in drawing the free body diagram. Note that while velocity is sketched on the initial figure, it is not included on the FBD itself.
Magnetic force is always perpendicular to both the motion of electric charges and the direction of the magnetic field. This means that magnetic force problems are inherently three-dimensional. The convention for drawing three dimensions on a two-dimensional piece of paper is that an “X” represents a vector into the plane of the paper and a “ ∙ ” represents a vector directed out of the paper.
You always need to draw a free body diagram for Newton’s Second Law problems and magnetic force problems are no exception. However, when a magnetic force is present, you have the additional step of using the 3-step right hand rule to find the direction of that force.
The point of the right hand rule is to allow you to find the direction of F or v or B when you know the direction of the other two. The biggest difficulty that most students have is fixing their hand in one orientation rather than letting the two known vectors determine the position of their hand. So here, you know v and B, and so you should let them determine the position of your fingers and discover where that puts your thumb.
Some orientations are awkward—don’t hesitate to turn your paper. If you have problems with the 3-step right hand rule, make a habit of always turning your paper so that the motion of the charge goes to the top of the page. This allows you to turn your wrist freely. Mark the direction you want to find on your paper before you rotate it back to the original position.
In the 3-step right hand rule, your thumb gives the direction of the force on a positive charge, your index finger points with the motion of the charge, and your palm (or bent remaining three fingers) point in the direction of the magnetic field. So in this case, point your palm or bent fingers into the paper while your index finger points to the right. In this orientation, your thumb points up toward the top of the paper so the force on a + charge is up. The force on a – charge is the reverse, or down.

Source of image: Encyclopedia Britannica Inc., http://www.britannica.com/
Some texts teach you to use your left hand for negative charges and your right hand for positive charges, others teach you to always use your right hand and reverse the answer if your charge is positive. Either approach will give the same answer.
Magnetic force depends on sine of the angle between magnetic field and velocity. (For those of you in a calculus based class, magnetic force is the cross product of magnetic field and velocity.)
In other words, any component of velocity that is parallel to the magnetic field gives no contribution to magnetic force (a charge moving parallel to the field will continue at constant velocity) and any component of velocity that is perpendicular to magnetic field results in a force perpendicular to velocity and causes the charge to move in a circle.
In this problem, the electron’s velocity is entirely perpendicular to the magnetic field.
You can solve Newton’s Second Law for any point in the motion. I chose to use the initial point (where magnetic field is first turned on.)
Acceleration of an object moving in a circle at a constant speed is inward toward the center of the circle (the negative y-direction as the FBD is shown here) and has a magnitude of v2/r.
The magnitude of magnetic force on a moving charge is qvB sinθ. θ is the angle between v (to the right) and B (in), or 900 in this case. Sin(900) = 1.
At the point in the circle where I chose to solve the problem, the force is directed down, or the –y direction.
Dividing both sides by -v
Mass of the electron can be found in your text or on line.
Charge of the electron can be found in your text or on line. Don’t include the – sign on charge or you will double count the direction of force. (The equation qvB sinθ gives the magnitude of the force and you put in the direction according to your coordinate system.)
(kg m/s)/(C∙T)
= (kg m/s)/(C∙kg/(C∙s))
= (kg m/s)/(kg/s)
= m
Why isn’t velocity included on the free body diagram?
The free body diagram is a stylized drawing to help you visualize the cause of acceleration (changes to velocity), and to directly map the drawing into the left hand side (ΣF) of Newton’s Second Law. Change in velocity is the effect of the forces, and therefore is not included on the list of forces.
Why aren’t other forces such as gravity included on the free body diagram?
The mass of the electron is so small that gravity is much smaller than the magnetic force. You do not have any information about whether the electron is in air or a vacuum or on a surface, and so the best that you can do is to describe the effect that the magnetic force has on the electron’s motion.
