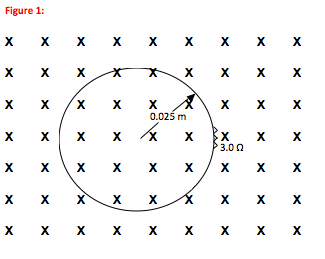
A circular loop of wire has a radius of 0.025 m and a resistance of 3.0 Ω. It is placed in a 1.6 T magnetic field which is directed in through the loop as shown and then turned off uniformly over a period of 0.10 s. What is the current in the wire during the time that the magnetic field changes from 1.6 T to zero?
-
In this problem, you are asked to find the current in a loop without a battery in it. There are two ways to cause current—you can directly drive it with a battery (or potential difference) or you can induce a current by changing the magnetic flux through a loop.
So this is an induction problem. Current in this loop is due to the changing magnetic flux through that loop. -

In induction problems, you need to work with the direction of any known vectors (such as field or current). So your picture should be a sketch of the actual situation with vectors labeled. All of this information (and more) is provided in the picture given in the problem, so no additional picture is needed.
Hint: Make sure the picture makes sense. Could you draw it from the text in the problem? -
Magnetic induction problems always begin with the definition of EMF:
EMF = -N ΔΦ/Δt = -N Δ(BA cosθ)/Δt (Calculus students use d rather than Δ.)
In this case, once you know induced EMF you will need to use it in ΔV = IR to find current. However, if you don’t recognize that step now it is fine. It will become apparent as you solve the problem. The most important thing is to recognize that you begin with induction.
Note that you will also need to use the right hand rule to determine the direction of current. -
Step 1:


Now that you know the EMF, continue to step 2 to find the current in the wire.
------------------------------------------------------------------------------
Step 2:

EMF plays the same role in a circuit as potential difference (ΔV) does. Therefore,
ΔV = IR
EMF = IR
I = EMF/R = (0.031 V)(3.0 Ω) = 0.010 AContinue to step 3 to find the direction of this current.
------------------------------------------------------------------------------
Step 3:

1. The direction of the induced current is such that
2. its magnetic field opposes
3. the change in the original magnetic field.
3. The change in the original magnetic field is up out of the paper ( ∙ )
2. Opposing "out of the paper" is "into the paper" (X)
1. From the two-step right hand rule, a magnetic field into the paper is caused by a clockwise current.
How did you figure out the change in magnetic field?
The original magnetic field is into the paper getting weaker. Therefore, the change in magnetic field is out of the paper
(original + change = final
or
into + out = 0).How did you use the right hand rule?
The direction of the magnetic field B due to current I is given by the two step right hand rule:
1. Point your thumb in the direction of either I or B, whichever is straight.
2. The direction your fingers curl gives the direction of the remaining vector (either I or B.)
or
“Thumb straight, fingers curl.”In this case, you know that the magnetic flux through the loop changes because the magnetic field changes.
The total resistance of the loop is 3.0 Ω. You can treat the loop as an ideal (resistance-free) loop with a 3.0 Ω resistor in it.
The problem describes a circular loop of wire of 0.025 m radius.
Problems involving magnetic force or field are inherently three-dimensional. The convention for drawing three dimensions on a two-dimensional piece of paper is that an “X” represents a vector into the plane of the paper and a “ ∙ ” represents a vector directed out of the paper. In this case, the magnetic field is directed into the loop (which was drawn in the plane of the paper.)
Φ is magnetic flux through a loop. You only have an induced EMF when flux changes through the loop.
Magnetic flux through a loop depends on the strength of the magnetic field, the size of the loop, and the orientation of the loop with the magnetic field.
The – sign in this equation is merely to remind you that the induced current is such that its magnetic field opposes the change in flux through the loop. It does not tell you the direction of either EMF or current.
“N” is the number of wraps in the loop of wire. In this case, it is a single loop.
Both the size of the loop and its orientation remain the same—they can be factored out of BA cosθ and pulled outside the Δ__/Δt operator. If this doesn’t make sense to you, it is fine to leave them in. Then you will have (BA cosθ)final - (BA cosθ)initial, which is equivalent to Acosθ(Bfinal – Binitial) when A and θ don’t change.
θ is the angle between B and A. The direction of A is defined as the direction of the normal to the plane of the loop—picture this as the direction of a pencil that is pushed through the paper. In this case, the normal to the loop is out of the paper, B is into the paper, so θ = 1800 and cos(1800) = -1.
The area of a circle is πr2.
Remember, Δ means final – initial.
m2s/T
= mv2s/(V∙s/m2)
= V
Note that you can find MKS units for Tesla on the internet.The original magnetic field is into the paper getting weaker. Therefore, the change in magnetic field is out of the paper
(original + change = final
or
into + out = 0).To oppose the change in magnetic field, you need a magnetic field coming out of the paper. In other words, a field out of the paper acts in the direction needed to try to keep the flux constant—it opposes the inward change.
The direction of the magnetic field B due to current I is given by the two step right hand rule:
1. Point your thumb in the direction of either I or B, whichever is straight.
2. The direction your fingers curl gives the direction of the remaining vector (either I or B.)
or
“Thumb straight, fingers curl.”How do you know which right hand rule to use?
Any time you need to relate a magnetic field to the current that causes it, you use the two step right hand rule (there are two vectors: current and field.)
Any time you need to consider the force on a moving charge (or current) in an external magnetic field, you use the three step right hand rule (there are three vectors: force, motion and field.)How do you work induction problems in which the size or orientation of the loop changes?
You work them in exactly the same way. When you get to the point in the problem where you need to put in numbers and solve the equation, either A or cosθ will remain inside the Δ__/Δt operator, and the other variables remain constant. The approach is identical! -

In this problem, you are asked to find the current in a wire that does not contain a battery. In general, if there is no source of voltage difference in a circuit, you should consider induction as the cause of current even though the word induction was not used in the problem. In this case, the magnetic field changes and so you have a changing magnetic flux through the loop. A changing magnetic flux results in an EMF, which has the same effect in a circuit as a voltage difference.
