You push a 15 kg box of books 2.0 m up a 25o incline into the back of a moving van. The box moves at a constant velocity if you push it with a force of 95 N. Find a) the work done by normal force on the box, b) the work done by your push on the box, c) the work done by gravity on the box, and d) the work done by friction on the box. (Assume your push is parallel to the incline.)
-
In this problem, you are given information about forces on an object and the distance it moves, and you are asked for work. Force and work are closely related through the definition of work. Parts a), b), and c) are definition problems.
You are not directly told the magnitude of the frictional force. Therefore, part d) is not a definition problem. However, you do know the motion of the box. Work and motion are related through the Work-Energy Theorem in the same way that force and motion are related through Newton’s Second Law. If you don’t recognize that there will be a Work-Energy Theorem component to this problem now, that is fine. It will become apparent when you get to part d) of the problem.
-
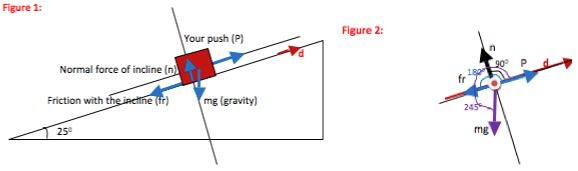
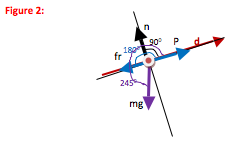
Because the definition of work depends on the angle between force and displacement, it is helpful to draw a picture even though this is a definition problem. The picture needs to show that angle for each force in question. To show the angle, begin in the direction of displacement and rotate counter-clockwise to the force. It is fine to draw a separate picture for each force, rather than color-coding the angles as done here.
-
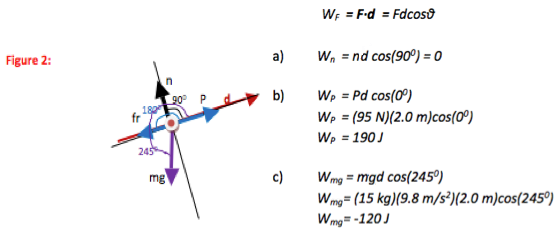
In equation form, the definition of the work done by force F is
WF = F∙d = Fdcosθ
This is the only relation that you need for parts (a-c) of this problem.
In part d), you are not given information about the size of the frictional force. You can find it using Newton’s Second Law and then use the definition of work once again. However, whenever you are asked about work it is easier to use the Work-Energy Theorem in place of Newton’s Second Law if possible. In equation form, the Work-Energy Theorem is
Wnet = ΔKE -
Step 1
If you did not recognize that you would need to use the Work-Energy Theorem to solve part d) of this problem earlier, you would see it now. You do not know the size of the frictional force and so cannot just plug it into the definition equation. Continue to Step 2 to solve part d) using the Work-Energy Theorem.
Step 2
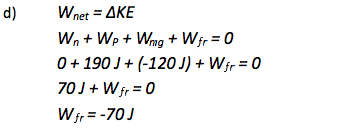
Part d) of this problem asked for the work done on the box by the frictional force. No further mathematical solution is necessary.
Can’t I solve for friction using Newton’s 2nd Law and plug that into the definition of work?
Although you are not told about the size of friction, you are given information about the motion of the box. That information will allow you to use the Work-Energy Theorem to find work done by friction as done in this example. An alternate way to find the work done by friction is to solve for the frictional force using Newton’s Second Law and plug that value into the definition of work. Although the Newton’s Law approach is equally correct, it will always save time and effort to use the Work-Energy Theorem when you can.
Why did you show d on the drawing?
It is correct that only forces should be shown on a free body diagram. However, this is a definition of work problem and not a force problem, so you should draw a picture appropriate for work rather than a free body diagram. Work depends on force, the distance moved, and the angle between force and displacement, so your drawing should reflect those three quantities.
How do you know the size of each angle?
Normal force acts perpendicular (90o) to the incline.
Friction is opposite, or anti-parallel, to the direction of motion. Therefore, θ is 1800 and not 0. A 00 angle means that force is in the same direction as displacement.
The angle between displacement and gravity is 270o (3/4 the way around the circle) minus the 25o angle of the incline. (You can see where to put the 25oangle by exaggerating the small and large angles on your drawing. In other words, 25o is less than half of a right angle, so draw the slope of the incline to be very small. Then you can see that mg makes a smaller angle with the –y axis than it does with the -x axis, and the smaller angle is 25o.)
The direction of displacement is up the incline. The 65o angle is the angle between moving down the incline and the direction of gravity. However, the magnitude of cos(65o) is equal to the magnitude of cos(245o). If you use the smaller angle, you must remember to put the sign of work in directly—the equation will not do it for you.Why do you use the 245o angle and not 65o?
The direction of displacement is up the incline. The 65o angle is the angle between moving down the incline and the direction of gravity. However, the magnitude of cos(65o) is equal to the magnitude of cos(245o). If you use the smaller angle, you must remember to put the sign of work in directly—the equation will not do it for you.
Why is 9.8 m/s2 positive?
OrWhy don’t you have to take the x-component of gravity only?
The F in the definition of work is the magnitude of the entire force F. Therefore, it is positive and you don’t have to worry about components. The cost term in the definition handles components for you.
What does “Wnet” mean?
“net” just means sum, so the net work is just the sum of the work done by all of the forces acting on the box.
How do you know ΔKE is zero?
The velocity of the box is constant. Therefore the change in its kinetic energy (Δ ½ mv2) is zero. Kinetic energy remains constant.
What does the negative sign for Wfr mean?
The negative sign indicates that the frictional force is acting against the motion of the box.
The direction of displacement, up the incline, needs to be shown on the figure because that is the reference point for θ. In other words, θ = 0 in the direction of displacement.
Even if part d) of the problem didn’t explicitly tell you that there is friction, you should suspect it is present because the box moves as a constant velocity up the incline. You can verify that suspicion with the Work-Energy Theorem or with Newton’s Second Law.
Normal force acts perpendicular (90o) to the incline.
Friction is opposite, or anti-parallel, to the direction of motion. Therefore, θ is 1800 and not 0. A 00 angle means that force is in the same direction as displacement.
The angle between displacement and gravity is 270o (3/4 the way around the circle) minus the 25o angle of the incline. (You can see where to put the 25oangle by exaggerating the small and large angles on your drawing. In other words, 25o is less than half of a right angle, so draw the slope of the incline to be very small. Then you can see that mg makes a smaller angle with the –y axis than it does with the -x axis, and the smaller angle is 25o.)
The direction of displacement is up the incline. The 65o angle is the angle between moving down the incline and the direction of gravity. However, the magnitude of cos(65o) is equal to the magnitude of cos(245o). If you use the smaller angle, you must remember to put the sign of work in directly—the equation will not do it for you.Some books use Δx rather than d for displacement. Either is fine, and both refer to the same thing.
Some books use K as a symbol for kinetic energy, and others use KE or K.E. These are all equivalent and refer to the same thing.
The Work-Energy Theorem is directly derived from Newton’s Second Law. It restates the The Work-Energy Theorem is directly derived from Newton’s Second Law. It restates the same information in terms of work and kinetic energy instead of force and acceleration. information in terms of work and kinetic energy instead of force and acceleration.
Even though you don’t know the magnitude of the normal force, you can still use the definition of work to solve part a). The angle between normal force and displacement is 90o. Cos(90o) = 0, so normal force does not do any work on the box. You may have recognized this conceptually without doing the math.
Your push is in the same direction as displacement. In other words, the angle between them is 0.
The MKS unit for work and energy is the Joule (J). 1 J = 1 N∙m
The negative sign indicates that the gravitational force acts against the motion of the box. Because only two significant figures were given in the problem, only two were kept in the solution.
The F in the definition of work is the magnitude of the entire force F. Therefore, it is positive and you don’t have to worry about components. The cost term in the definition handles components for you.
The negative sign indicates that the frictional force is acting against the motion of the box.
The velocity of the box is constant. Therefore the change in its kinetic energy (Δ ½ mv2) is zero. Kinetic energy remains constant.
“net” just means sum, so the net work is just the sum of the work done by all of the forces acting on the box.
Why did you show “d” on the diagram? I thought only forces are on a free body diagram.
It is correct that only forces should be shown on a free body diagram. However, this is a definition of work problem and not a force problem, so you should draw a picture appropriate for work rather than a free body diagram. Work depends on force, the distance moved, and the angle between force and displacement, so your drawing should reflect those three quantities.
Why don’t you need to divide the force vectors into components?
It is true that only the component of force parallel to displacement contributes to the work done. However, the equation for work done by force F, WF = Fdcosθ (F∙d for those of you in the calculus class,) does that for you. Because θ is the angle between force and displacement, Fcosθ is the component of force parallel to displacement.
How did you know the size of each angle?
Because the x- and y-axes form a 90o angle, the angles between distance moved and normal force, your push, and friction are straightforward. The angle between distance moved and gravity is 270o (3/4 the way around the circle) minus the 25o angle of the incline. (You can see where to put the 25o angle by exaggerating the small and large angles on your drawing. In other words, 25o is less than half of a right angle, so draw the slope of the incline to be very small. Then you can see that mg makes a smaller angle with the –y axis than it does with the -x axis, and the smaller angle is 25o.)
Can’t I use the 65o angle for gravity rather than the 245oangle?
The direction of displacement is up the incline. The 65o angle is the angle between moving down the incline and the direction of gravity. However, the magnitude of cos(65o) is equal to the magnitude of cos(245o). If you use the smaller angle, you must remember to put the sign of work in directly—the equation will not do it for you.
I don’t know the size of the frictional force. How can I answer part d)?
Although you are not told about the size of friction, you are given information about the motion of the box. That information will allow you to use the Work-Energy Theorem to find work done by friction as done in this example. An alternate way to find the work done by friction is to solve for the frictional force using Newton’s Second Law and plug that value into the definition of work. Although the Newton’s Law approach is equally correct, it will always save time and effort to use the Work-Energy Theorem when you can.
Help. I got a negative answer for work done by gravity and for work done by friction. Is that ok?
Yes. Although work and energy are not vector quantities, they do have positive and negative values (just as other scalars such as height and temperature do.) In this case, a positive value of work means that the force acts with the motion of the object, and a negative value of work means that the force acts against the motion.
-
In this problem, we were asked to find the work done on a box by a variety of forces. When you know the magnitude of a force, the work is does is given by:
WF = Fad = Fdcosθ
F in this equation is the magnitude of the force, d is total displacement, and θ is the angle between force and displacement. You do not need to divide any vectors into components for this definition. Negative values of work indicate that the force acts against the motion of the object.
Total work done on an object is related to the change in kinetic energy of the object, just as total force on an object is related to the acceleration.
Wnet = ΔKE
This relation will be restated as Conservation of Energy and used in a wide variety of problems. However, in this form, it is handy for finding the work done by an unknown force.
- Why did you show “d” on the diagram? I thought only forces are on a free body diagram.
- Why don’t you need to divide the force vectors into components?
- How did you know the size of each angle?
- Can’t I use the 650 angle for gravity rather than the 2450angle?
- I don’t know the size of the frictional force. How can I answer part d)?
- Help. I got a negative answer for work done by gravity and for work done by friction. Is that ok?
