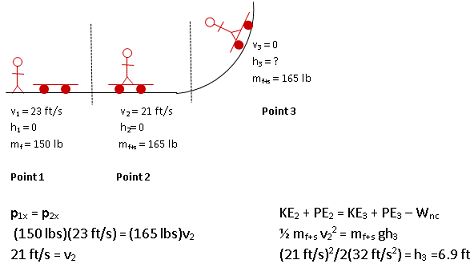
You are helping your friend prepare for the next skateboard exhibition by determining if the planned program will work. Your friend will take a running start and then jump onto a heavy-duty 15-lb stationary skateboard. The skateboard will glide in a straight line along a short, level section of track, then up a sloped concrete wall. The goal is to reach a height of at least 10 feet above the starting point before coming back down the slope. Your friend's maximum running speed to safely jump on the skateboard is 23 feet/second. Your friend weighs 150 lbs.
This problem was used with permission of Dr. Ken Heller of the University of Minnesota Physics Education Research Group.
-
In this problem, you are asked to find the height to which your friend rises when he or she jumps on a skateboard with a running start. Any time you are asked to relate speed and position of an object, you should check to see if you can use Conservation of Energy to solve the problem. In this case, you have an unknown amount of force that takes energy out of the system when your friend collides with the skateboard and so you cannot track non-conservative work during the collision. So this is not a one-step problem.
However, the unknown energy loss occurs during a collision. Any time you are asked to find speed or velocity of an object just before or just after a collision or separation, you can likely use Conservation of Momentum to solve that part of the problem.
This, then, is a two part problem. Momentum is conserved as your friend collides with the skateboard, and energy can be tracked as the skateboard goes up the incline. If you do not recognize both parts of the problem before you begin, that is fine. You can start the problem with either momentum or energy and will quickly find that you need to do an additional analysis to complete the problem
You are asked about the height to which your friend and the skateboard rise. Gravitational potential energy is associated with height, which suggests that energy can be used once your friend is on the skateboard.
Collisions or separations do not need to be dramatic. You can use Conservation of Momentum on any collision/separation problem in which Fextermal Δt = 0 over the time of the interaction. In other words, the internal force of interaction just needs to be significantly larger than the external forces on the system.
Momentum is conserved on a system only when the net force on that system is small enough that Fextermal Δt is essentially zero. (This comes straight from Newton's Second Law and the definition of acceleration.) In the case of a collision or separation, the force between the interacting objects or pieces is quite large. So the momentum of each individual object changes because of the force between them. (In this case, the velocity of your friend and the velocity of the skateboard each change due to the collision force.) But the net effect of the internal force on the two object system is zero (think of Newton's Third Law.)
In this case, the force of the collision is much larger than any kinetic friction on the skateboard during the collision. So the conditions for using Conservation of Momentum are met.
When a non-conservative force acts, it takes energy in or out of the system. If you know the size of the force and the distance over which it acts, you can calculate the amount of energy that enters or leaves the system by
W = F Δx cosθ
and you only need Conservation of Energy to understand the problem. In this case, you do not know the size of the force that brings your friend to rest on the skateboard and so an unknown amount of energy leaves the system during this collision.
Can this problem be worked using dynamics?
Why would you want to? It is generally possible to work Conservation of Energy and Momentum problems using a combination of Newton's Second and Third Laws and the kinematic relationships, but it is always easier to use energy and momentum when you can.
Why do you have to use Conservation of Momentum? Can't you just track energy?
In order for your friend to come to a stop relative to the skateboard, normal force and friction between your friend and the skateboard must do work. In other words, energy is lost from the friend/skateboard system during the collision. In general, whenever there is a collision or separation between objects, energy is lost from the system.
-
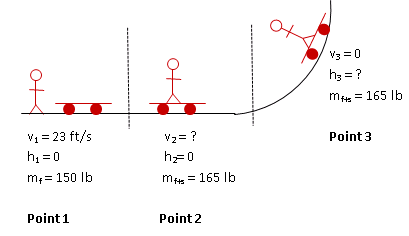
For Conservation of Momentum problems, you always draw a picture of the system immediately before the collision or separation and another picture immediately after (Points 1 and 2.) Because momentum depends on mass and velocity, label all mass and velocity information on the pictures. This helps to avoid mistakes as you fill into the equation later.
For Conservation of Energy questions, you want to show the velocity and position information at all points over which you track energy (Points 2 and 3.)
How do you know to pick your friend and the skateboard as a single system?
It is clear that after your friend lands on the skateboard they behave as a single object. Before the "collision", however, they move separately. But remember, whenever you have a collision between objects, or a separation of one object into smaller objects, you can probably treat the momentum of that multiple object system as being conserved around the time of the collision/separation even though the momentum of each individual object changes.
The reason for this is that momentum is conserved on a system only when the net force on that system is small enough that Fextermal Δt is essentially zero. (This comes straight from Newton's Second Law and the definition of acceleration.) In the case of a collision or separation, the force between the interacting objects or pieces is quite large. So the momentum of each individual object changes because of the force between them. (In this case, the velocity of your friends goes down and the velocity of the skateboard goes up as a result of the collision.) But the net effect of the internal force on the two object system is zero (think of Newton's Third Law.) So if we treat the interacting objects together as a single system, momentum of that larger system only changes by Fextermal Δt, or about zero. Δt is the time over which the collision or separation takes place and is small.
How do you know the shape of the inclined part of the track?
As long as friction doesn't take energy out of the system, the shape of the track doesn't matter. The only relevant information is the final height.
Before your friend jumps on the skateboard, your friend and the skateboard move separately and so are treated as two objects with their own mass. Once your friend has landed, they move together and so behave as a single object with the combined mass of 150 lb + 15 lb = 165 lb.
I chose the lowest point in this problem (the starting point) to be h = 0. I did not take the final height to be 10 feet because I do not know how far up your friend will go. The question asks if this set up will give a final height of at least 10 feet, and so I am solving the problem for the final height.
Your friend's speed before jumping on the skateboard is 23 ft/s.
Because energy is lost during the collision of your friend and the skateboard, you cannot assume that v2 is 23 ft/s. (In fact, even if energy was not lost the speed would not be 23 ft/s because the mass of the friend/skateboard system is larger than the mass of your friend.) You need to solve the Conservation of Momentum equation to find out how fast your friend and the skateboard move together.
As your friend and the skateboard move up the ramp, they will slow until they reach a stop and come down again. They are stopped at the highest point.
The first point of interest in this problem is just before your friend jumps on the skateboard. This point will be used as you compare momentum before the collision to momentum just after the collision.
The second point of interest in this problem is just after your friend has landed on the skateboard. This point will be used as you compare momentum before the collision to momentum just after the collision. It will also be used as you track the energy of the friend/skateboard from energy of motion to gravitational potential energy.
The third point of interest in this problem is the highest point to which your friend and the skateboard rise. This is the point about which the problem asks.
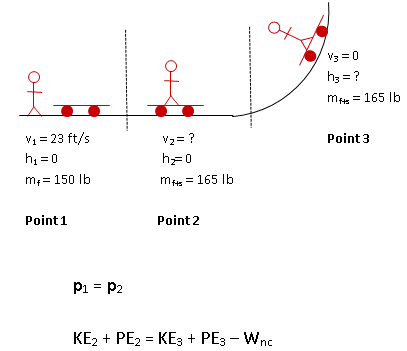
Any time you understand the motion of a system for which Fextermal Δt is about 0, you can usethe Conservation of Momentum equation. Practically, this means that any time you want to explore what happens during a collision or explosion you will consider Conservation of Momentum.
Any time you understand the motion of an object by looking at its energy, you begin with the Conservation of Energy equation. This form of the equation works whenever you can track Wnc.
In this problem, we know information about Point 1 and want to learn about Point 3. Therefore, we will begin with the Conservation of Momentum equation--we can use information about Point 2 to learn about Point 2. From their, energy at Point 2 can be tracked to learn about Point 1.
Once your friend has landed on the skateboard, there is virtually no non-conservative work done on the system. The wheels of the skateboard roll due to static friction. As long as there is little drag or slipping, the energy taken out of the system is negligible. Note that this is not true during the collision. When your friend lands on the skateboard, a significant and unknown amount of energy is dispersed. We cannot track Wnc during the time that period of time.
After your friend lands on the skateboard, they move together with a speed of 21 m/s. Scroll down to find the maximum height to which they can rise up the ramp.
How do you know which points to compare?
I know that energy is lost from the friend/skateboard system during the collision, but that momentum is conserved during that time. Momentum is not conserved as they move up the ramp because the force of gravity does work to slow them down. Therefore, I can only compare momentum just before and just after the collision.
Why did you treat the person and skateboard separately before the collision and together after?
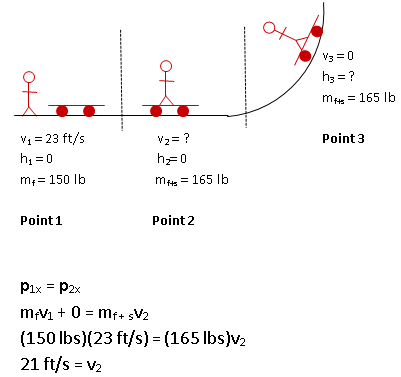
I didn't, really. For this problem, I am tracking the momentum (and, in Step 2, the energy) of the friend/skateboard system. Before the collision, they move separately and so each has its own velocity. After the collision, they move with the same velocity. mfv + . msv = . mf+sv. Just make sure if you work the problem this way that you assign both pieces the same velocity.
Momentum is a vector and so you need to treat components separately. Because the motions considered in this part of the problem are along a single direction, I chose that to be my x- axis.
After the collision has taken place, an unbalanced component of gravity acts as your friend and the skateboard move up the ramp. In other words, over that portion of the motion gravity does significant work and momentum is not conserved. Therefore, I can only consider Conservation of Momentum over the time of the collision--Point 1 to Point 2.
Before the collision, the skateboard is at rest. ms(0) = 0.
After the collision, your friend and the skateboard move together. Therefore, I chose to treat them as a single object with a combined mass of 165 lb. It is equally fine to treat them in two terms. Velocity will be the same for both.
----------------------------------------------------------------------------------------------
Step 2
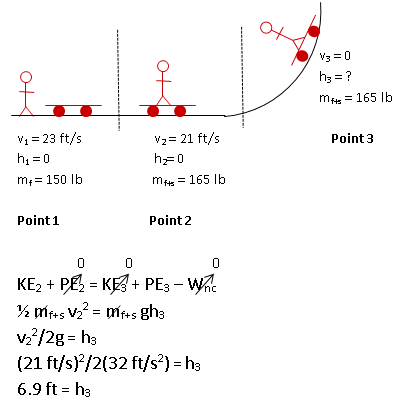
If your friend jumps on the skateboard from a running start at 23 ft/s, he or she will only rise up the ramp about 7 feet, falling short of the desired 10 feet for the program.
Why did you use 32 ft/s2? Why is it positive?
The information given in the problem was in English units. It is much easier to use g in English units than to convert all of the information in the problem to metric units. The sign of gravitational potential energy comes from the sign of height. g in the definition of gravitational potential energy refers to the absolute value.
How do you know which points to compare? Why can't you compare energy between Points 1 and 3?
Although the energy of the universe is always conserved, it can enter or leave any given system. In this case, energy leaves the friend/skateboard system when your friend lands on the skateboard. Because I do not know the size of the force that brings your friend to rest with respect to the skateboard, I cannot track the energy that left through Wnc. Therefore, I do not have enough information to compare the energy in the system at Point 1 to the energy in the system at Point 3. I do, however, know that no significant amount of energy leaves the system after the collision has taken place. Therefore, I am able to track energy between any two points after the collision.
Why didn't you have to consider energy loss due to friction?
A wheel rolls rather than slides when the frictional force on the bottom of the wheel holds it in place as the top of the wheel "falls" forward. In other words, when wheels roll without slipping there is no sliding friction and friction does not take energy out of the system.
Why didn't you have to consider the shape of the ramp?
The amount of work done by gravity (the amount of energy transformed from kinetic to gravitational potential energy) depends only on the vertical distance covered. As long as there is no non-conservative force such as friction taking energy out of the system, the length (shape) of the actual path covered doesn't matter.
I chose h = 0 to be at the bottom of the ramp. Therefore, the gravitational potential energy at Point 2 is 0.
A wheel rolls rather than slides when the frictional force on the bottom of the wheel holds it in place as the top of the wheel "falls" forward. In other words, when wheels roll without slipping there is no sliding friction and friction does not take energy out of the system. Wnc, therefore, is zero.
Mass in this equation refers to the mass of your friend plus the skateboard because they move together up the ramp. Mathematically, because the same mass occurs in all terms, it divides out.
In the first Solve step of this problem, we found that your friend and the skateboard move with a speed of 21 ft/s after your friend has landed on the skatebloard. Make sure you do not use 23 ft/s, which is the speed of your friend before energy was lost from the system. Be sure, also, that you remember to square the velocity.
The information given in the problem was in English units. It is much easier to use g in English units than to convert all of the information in the problem to metric units. The sign of gravitational potential energy comes from the sign of height. g in the definition of gravitational potential energy refers to the absolute value.
The choice of coordinate system is yours. Because I chose height to be zero at the bottom of the ramp, the answer that I get for h3 will be the height of the ramp above the level section of track.
As your friend and the skateboard move up the ramp, they will slow due to the gravitational force. Once they slow to a stop, they will then begin moving back down the incline. Their speed at the highest point, then , is zero.
Although this problem asked you to find the height your friend could move up a ramp given an initial running speed, you are not able to compare energy at the start and the end of the problem because an unknown amount of energy is lost from the system as your friend lands on the skateboard. The energy chain for this part of the motion is
kinetic energy of your friend --> kinetic energy of your friend and the skateboard + heat/sound
You can, however, compare momentum during the collision because no external force (in this case friction, normal force on the skateboard, gravity) does significant amount of work on the system during the time of the collision.
Following the collision, the energy chain is
kinetic energy of your friend and the skateboard --> gravitational potential energy of your friend and the skateboard
and so energy can be tracked for that portion of the motion.
Note that a height of 6.9 feet is reasonable and makes sense as the solution to this problem.
- Why do you have to use Conservation of Momentum? Can't you just compare the kinetic energy of your friend to the gravitational potential energy of your friend on the skateboard?
- Don't you have to know how much friction is present?
- How do you pick h = 0?
- How do you know to treat your friend and the skateboard together as a single system?
- Can this problem be worked using dynamics?
- What are the conversions between feet and meters and between pounds and Newtons?
Why do you have to use Conservation of Momentum? Can't you just compare the kinetic energy of your friend to the gravitational potential energy of your friend on the skateboard?
In order for your friend to come to a stop relative to the skateboard, normal force and friction between your friend and the skateboard must do work. In other words, energy is lost from the friend/skateboard system during the collision. In general, whenever there is a collision or separation between objects, energy is lost from the system.
Don't you have to know how much friction is present?
An unknown amount of friction takes energy out of the friend/skateboard system during the collision. This is why you cannot use Conservation of Energy alone for this problem. As long as the skateboard rolls without slipping, friction between the skateboard and the cement does not do any work and therefore does not take energy out of the system.
How do you pick h = 0?
All that matters for describing motion and energy is that you explicitly state where your reference point is. In this case, I chose the lowest height in the situation to be h = 0.
How do you know to treat your friend and the skateboard together as a single system?
It is clear that after your friend lands on the skateboard they behave as a single object. Before the "collision", however, they move separately. But remember, whenever you have a collision between objects, or a separation of one object into smaller objects, you can probably treat the momentum of that multiple object system as being conserved around the time of the collision/separation even though the momentum of each individual object changes.
The reason for this is that momentum is conserved on a system only when the net force on that system is small enough that Fextermal Δt is essentially zero. (This comes straight from Newton's Second Law and the definition of acceleration.) In the case of a collision or separation, the force between the interacting objects or pieces is quite large. So the momentum of each individual object changes because of the force between them. (In this case, the velocity of your friends goes down and the velocity of the skateboard goes up as a result of the collision.) But the net effect of the internal force on the two object system is zero (think of Newton's Third Law.) So if we treat the interacting objects together as a single system, momentum of that larger system only changes by Fextermal Δt, or about zero. Δt is the time over which the collision or separation takes place and is small.
Can this problem be worked using dynamics?
Why would you want to? It is generally possible to work Conservation of Energy and Momentum problems using a combination of Newton's Second and Third Laws and the kinematic relationships, but it is always easier to use energy and momentum when you can.
What are the conversions between feet and meters and between pounds and Newtons?
It doesn't matter. Why not just work the problem using English units? The acceleration of gravity in English units is 32 ft/s2.
