A 40 ft by 40 ft square house (with no basement) has outer walls that are 12 feet high. The roof rises to a height of 17 feet above the walls at the center, and the total area of windows and doors is 190 square feet. The house is insulated--the R-value of the insulation in the floor is 25 (ft2 0F hr/Btu), of the insulation in the roof is 55, and of the insulation in the walls is 15. Take the R value of the windows and doors to be about 5. The house is heated to 680F on a night when the outside air temperature is 200F and the windchill is 50F. If the house is well sealed against drafts and the furnace fails, about how long will it take for the inside temperature of the house to decrease to 650F? Take the ground temperature to be 500F, and assume there are no other sources of heat in the house.
-
At root, this is a heat transfer problem: you want to know how much time it takes place to lose enough heat for the house to cool 50.
You know that insulation in a house reduces the heat transfer by conduction, and so even if you were not explicitly given the R-values you should recognize that you need to calculate heat transfer by conduction. The problem states that the house is well sealed, which implies that you do not need to take convection into account. The third method of heat transfer is radiation. In this case, you do not have any information about the emissivity of the house and therefore cannot calculate the rate of heal loss by radiation. It is certainly true that convection and radiation do play a role. The house will cool faster than the rate that you calculate from conduction alone.
Note that you are not told in the problem how much thermal energy you need to transfer. This, then, is a two-part problem. Before you can find how much time it takes to transfer the energy, you need to find how much energy must leave the house as it cools 50F.
R-value is a measure of a material's resistance to heat transfer by conduction. Energy transfer by conduction takes place when faster moving molecules collide electromagnetically with slower molecules, giving some of their energy to the slower molecules.
Energy transfer by convection requires physical motion of a warm fluid such as air. In this case, if the house is well sealed, air does not leave the house and so energy is not convected from inside the house to the outside.
Human beings radiate about 100 J of energy per second, the same as a 100 W light bulb. Incandescent light bulbs give off about 90 % of their energy as heat rather than visible light. Appliances, too, convert some of the electric energy into thermal energy.
All objects radiate energy as electromagnetic waves due to their temperature. In addition to the dependence on temperature, the rate at which energy is radiated depends on the color and other factors that influence the effectiveness with which an object radiates. This information is summarized as emissivity of the object--emissivity is not a universal constant but is object specific.
Even though the house is getting cooler rather than warmer, energy is being transferred. In this case, the transfer is of thermal energy from the inside of the house to the outside.
My book does not talk about R-values. What are other ways this question could be phrased?
R-values allow you to compare the insulating properties of different materials. They take both the thermal conductivity of the material and its thickness into account. R is defined as thickness/Κ. This problem could also be written to include information about the thickness and composition of the insulation.
I don't see that this is a two-part problem. Isn't it just heat transfer?
This may become more clear as you select the relationships that you will use to calculate the time, or it may not be clear until you have a partial solution. If that is the case, make sure to spend some time thinking about the integration of the two parts before you leave this example. If the R-values tipped you off to consider heat transfer by conduction, it is great to start the problem there. As you get into it, you will realize that you do not know Q and can reconsider the need to relate energy and temperature change at that point.
How is time involved?
When we talk about "heat transfer," we mean the time rate at which thermal energy moves from one region to another. More insulation slows the rate at which the energy moves, but it does not prevent energy transfer.
-
A picture of the house is not particularly useful. There is no loss to understanding if you skip this step. On the other hand, it might help you to visualize the information about the shape of the roof.
How did you know the shape of the roof?
The problem states the the roof is higher in the center than on the sides. The simplest way to do that is with a roof that is made of two rectangles that slope upward and toward the center.
Even though the ground is warmer than the air, it is still colder than the inside of the house. Therefore, thermal energy will conduct through the floor and into the ground.
-
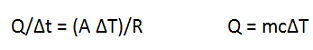
There are two versions of the relation that quantizes heat transfer by conduction. Because R-values were specified, I chose that version rather than Q/Δt = (A ΔT)/L. In this problem, you are not told how much energy is transferred. However, you are told that the temperature of the house falls and so you also need the equation that relates energy to temperature change.
Are the Q's in these equations the same?
Yes. The second equation describes how much energy leaves the house as it cools and the first describes the rate at which that amount of energy leaves.
Are the ΔT's in these equation the same?
No. ΔT in the first equation describes the temperature difference across the walls of the house. ΔT in the second equation refers to how much the temperature inside the house changes. Note that Δt refers to a time interval and not temperature.
As the house cools, thermal energy leaves the house. The amount of energy that leaves is proportional to the drop in temperature of the interior of the house.
Q/Δt represents the rate at which energy leaves the house. That rate is proportional to the temperature difference between the inside and outside air.
-

The first step in this problem is to determine how much energy needs to leave the house in order for the temperature to drop 3 0F.
What the heck is an "lbm"?
That is a great question, and I had to look it up myself. Because R-values are given in English units, I searched for c in English units. Because I didn't recognize lbm, I looked it up. It is the mass of an object in English units--I learned English mass as being a "slug." With either name, English mass is weight (mg) of the object in pounds, divided by 32 m/s2 (g in English units).
Why did you use English units?
In this case, the values that were given in the problem were in English units. When I searched for the needed constants, I just specified the units that I wanted (e.g. "in Btu") and saved myself the stop of converting from English to metric units.
Why didn't you use 3.0 x 108 for c?
c in this case refers to heat capacity and not to the speed of light. Make sure to understand the meaning of each symbol in your equations.
If you did not recognize this as the first step that is okay. When you fill into the conduction equation (see the step below) you will notice that you do not know how much energy is lost. At that point, you will see that you need this step.
To find the mass of the air inside the house, I used the definition of density. According to my web search, the density of air in English units is 0.074887 lbm/ft3. Density x volume gave me the mass of the air. I calculated the volume of the house in two parts: first I found the volume of the house itself and then of the attic. I assumed a roof shape as shown in the Draw step.
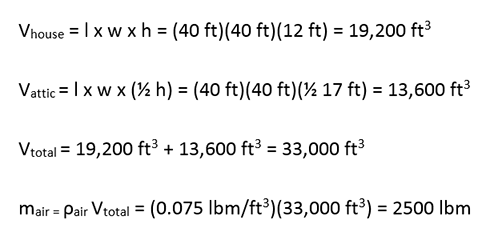
Make sure to understand the meaning of the symbols in the equations that you use. c in this case does not refer to the speed of light. It refers to the heat capacity of the material gaining or losing energy. I assumed the entire volume of the house was filled with air (in other words, I did not account for the varying heat capacity of the furnishings.) I did a web search for the "heat capacity of air in Btu" so that I would not have to do any unit conversions to use the numbers given in the problem.
The English units for heat capacity are Btu/lbm 0F. A Btu is a unit of energy, a lbm is a unit of mass, and 0F is a unit of temperature. You don't need to know this in advance. Just specify "English units" or any of the units that you do know when you do your search for the values you need.
This equation quantizes how much energy leaves the house. Therefore, ΔT refers to the temperature drop inside the house.
----------------------------------------------------------------------------------------------
Step 2

Once you know how much energy needs to leave the house in order for it to cool to 65 0F, you can calculate how long it takes the energy to leave.
Why did you use a different ΔT for the floor?
The ground is at at a temperature of 50 0F compared to 5 0F for the air surrounding the walls and roof.
Why did you use 50 and not 200 for the outside air?
If it is perfectly still, the air around a warm object or being will warm up. This reduces the rate of heat loss by conduction because ΔT is smaller. If the air is not perfectly still, not only is there more heat loss by convection but also no layer of warm air will build up. As a result, the object loses heat at a faster rate. The wind chill factor tells you the "equivalent" temperature--if the wind chill is 50F , that means you will lose heat at the same rate as you would on a calm day with a temperature of 50F .
Because energy conducts through all exterior surfaces of the house, you need to include the total outside surface area of the house. The house is not uniformly insulated, and so I broke up the area into pieces according to R-values. In other words, the total energy lost is the energy lost through the windows and doors plus the energy loss through the walls plus the energy loss through the roof plus the energy loss through the floor.
ΔT in this equation refers to the temperature difference across the surface through which the heat is being conducted. Note that as the house cools, the rate at which energy leaves is slightly reduced. For that reason, I used the average inside air temperature of (68 + 65)/2 = 66.5 0F for the temperature on the inside surfaces. The outside temperature for the floor is 50 0F, and I used 5 0F not 20 0F for the outside temperature of the walls and roof because wind chill means that you lose heat at the rate that you would in still air with the wind chill temperature.
Both the total surface area of the windows and doors and their average R-value are given in the statement of the problem.
4 walls have a total surface area of 4 x 40 ft x 12 ft = 1920 ft2. However, part of the walls are cut out for the windows and doors, so the surface area of the walls themselves is (1920 - 190) ft2 = 1700 ft2. The R-value for the walls is given in the statement of the problem.
The floor is 40 ft x 40 ft, or 1600 ft2. The R value of the floor is given in the statement of the problem.
I assumed the roof is made of two flat surfaces, each 40 ft x 26 ft as seen in the drawing below. The area of the roof, then, is 2 x 40 ft x 26 ft = 2100 ft2. The R-value of the roof is given in the statement of the problem.
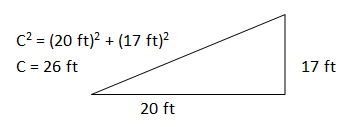
In this step, I divided all terms by Btu and cancelled the square feet in the numerator and denominator of the terms on the right hand side of the equation. Note that dividing by a fraction is the same as inverting and muliplying. This applies to units as well as to numbers and variables.
In this step, I multiplied each side by Δt and divided by 14,000 0F. Although numbers in the problem are given to two signifcant figures, I made enough estimations in the problem that it isn't really valid to keep the second significant figure in my answer. It is better to say it takes about an hour for the house to drop to 65 degrees.
-

The house cools because thermal energy is transferred across all surfaces of the house. The rate at which thermal energy is transferred depends on the amount of insulation as well as the temperature difference across each surface. For that reason, the total heat transfer had to be calculated as the sum of the parts--transfer through the walls, through the windows, etc.
Although physical constants could be looked up, a number of estimations were also made. For example, we assumed the entire house was filled with air and made assumptions about the shape of the roof. For that reason, it does not make sense to claim multiple significant figures.
What is the average R-value of the house?
It doesn't matter. Heat transfer is additive; the total heat lost from the house is equal to the heat lost through the roof plus the heat lost through the walls, etc. Add rates of heat transfer rather than averaging R.
How do I calculate heat loss by convection?
In this problem, you don't need to consider convection. The statement that the house is "well insulated" and the question "about how long" both suggest that you are to ignore convection. Of course, you know that no building is perfectly sealed and so the actual time it will take for the house to cool will be less than that which you calculate.
What is windchill?
If it is perfectly still, the air around a warm object or being will warm up. This reduces the rate of heat loss by conduction because ΔT is smaller. If the air is not perfectly still, not only is there more heat loss by convection but also no layer of warm air will build up. As a result, the object loses heat at a faster rate. The wind chill factor tells you the "equivalent" temperature--if the wind chill is 50F , that means you will lose heat at the same rate as you would on a calm day with a temperature of 50F .
