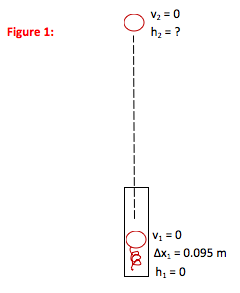
A child’s toy that is made to shoot ping pong balls consists of a tube, a spring (k = 18 N/m) and a catch for the spring that can be released to shoot the balls. When a ball is loaded into the tube, it compresses the spring 9.5 cm. If you shoot a ping pong ball straight up out of this toy, how high will it go?
-
In this problem, you are asked to find a vertical position of a ball when you are given its initial position on a spring. In both locations, the speed of the ball is zero.
If non-conservative forces are either known or small and if energy is converted from one form to another between the locations, then any time you relate speed and position of an object at two different points, conservation of energy is the most direct way to understand the problem.
In this case, you start out with stored energy in the compression of the spring and convert it to stored gravitational energy.
-
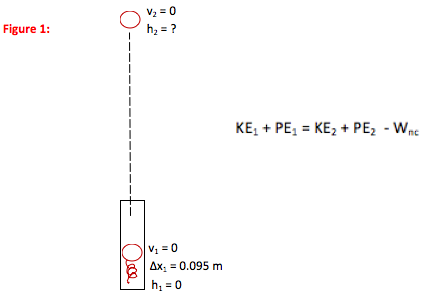
Any time you understand the motion of an object by looking at its energy, you begin with the Conservation of Energy equation.
-
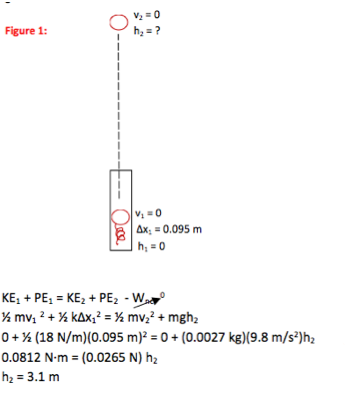
The ping pong ball rises to a height of 3.1 m above its position on the compressed spring. No further mathematical solution is needed for this problem.
Can this problem be worked using kinematics?
It is true that you are asked to describe motion in this problem. You also have information about the cause of the motion. So you could work it as a multi-part problem, using force to find acceleration to find velocity of the ball as it leaves the toy, and then use kinematics to find the height. (Note that spring force is not constant and so the process of going from force to acceleration to velocity of the ball as it leaves the toy would most easily take you back to the energy approach.) If you initially recognize that you have the information to work the problem with energy, you can solve it in a single step.
How do you pick h = 0?
All that matters for describing motion and energy is that you explicitly state where your reference point is. The initial position of the ball is slightly easier to use than the position of the ball when it leaves the toy, just because that means that h1 = 0. However, it is equally fine to use the location of the ball as it leaves the toy as the zero point. In that case, h1 = -0.095 m.
Why don’t you include a ½ kΔx2 term at Point 2?
You only include terms for the energy present. At point 1, the ball has potential energy due to its position on the compressed spring, but it does not have gravitational potential energy because it is at
h = 0. At point two, the ball is not at h = 0 and so it has gravitational potential energy. However, it is not stretching or compressing a spring, and so there is no spring potential energy.
This is not the way my book writes the Conservation of Energy equation. What is “Wnc”?
Wnc is any work done by non-conservative forces, such as friction or a push, which take energy in or out of the system of interest. Some books teach you to always think about this term, others only add it if it isn’t zero. Still others may write it as KE1 + PE1 + Eadded to the system = KE2 + PE2 + Eleaving the system. If there is no significant non-conservative force (as is the case in the first question) then all three versions of the equation are equivalent. Including Wnc in some form is more general and gives an equation that is true in all situations, including those with non-conservative forces.
Why is 9.8 m/s2 positive?
Gravitational potential energy can be either negative or positive, depending on whether the object is below or above the h = 0 point. In other words, the sign for PEg comes from the sign of h. + 9.8 m/s2 is always put in for g.
Why don’t you include an mgh term for Point 1?
At the starting point in this problem, the ball is at height = 0 against a compressed spring. Therefore, it has spring potential energy but does not have gravitational potential energy.
Why don’t you include a ½ kΔx2 term for Point 2?
At the top of the motion, the ping pong ball has a non-zero height but is not compressing or stretching a spring. Therefore, it has gravitational potential energy but does not have spring potential energy.
At the start of the problem, the ball is in the toy. The catch has not yet been released, and so the ball is at rest against the compressed spring. The spring force is a conservative force, and so the energy used to compress the spring has been stored in the system. Therefore, you know to include a spring potential energy term for the ball at Point 1.
You need to work any problem in a single unit system. Because the spring constant was given in MKS units, converted all values to meters and kilograms. I do conversions as part of drawing the picture so that I have all information in a ready-to-use format.
(9.5 cm)/(100 cm/m) = 0.095 mAt its maximum point, all of the kinetic energy of the ping pong ball has been converted into gravitational potential energy. v2 = 0.
Some books use PE for potential energy. Others use P.E. and others use U. All are equivalent and refer to the same thing.
Wnc is any work done by non-conservative forces, such as friction or a push, which take energy in or out of the system of interest. Some books teach you to always think about this term, others only add it if it isn’t zero. Still others may write it as KE1 + PE1 + Eadded to the system = KE2 + PE2 + Eleaving the system. If there is no significant non-conservative force (as is the case in the first question) then all three versions of the equation are equivalent. Including Wnc in some form is more general and gives an equation that is true in all situations, including those with non-conservative forces.
There are no significant non-conservative forces (like friction) present in this problem, and so the work done by non-conservative forces is about zero.
At the starting point in this problem, the ball is at height = 0 against a compressed spring. Therefore, it has spring potential energy but does not have gravitational potential energy.
At the top of the motion, the ping pong ball has a non-zero height but is not compressing or stretching a spring. Therefore, it has gravitational potential energy but does not have spring potential energy.
Google tells me that the mass of a ping pong ball is 27g.
(2.7 g)/(1000 g/kg) = 0.0027 kgGravitational potential energy can be either negative or positive, depending on whether the object is below or above the h = 0 point. In other words, the sign for PEg comes from the sign of h. + 9.8 m/s2 is always put in for g.
The values for Point 1 can be put into the equation directly from your picture.
The values for Point 2 can be put into the equation directly from your picture.
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
How do you know v2 = 0?
As the ping pong ball goes up, its kinetic energy is converted to gravitational potential energy. At its highest point, all kinetic energy has been converted to gravitational potential energy, so velocity at that point is zero.
How do you pick h = 0?
All that matters for describing motion and energy is that you explicitly state where your reference point is. The initial position of the ball is slightly easier to use than the position of the ball when it leaves the toy, just because that means that h1 = 0. However, it is equally fine to use the location of the ball as it leaves the toy as the zero point. In that case, h1 = -0.095 m.
Why don’t you include a ½ kΔx2 term at point 2?
You only include terms for the energy present. At point 1, the ball has potential energy due to its position on the compressed spring, but it does not have gravitational potential energy because it is at
h = 0. At point two, the ball is not at h = 0 and so it has gravitational potential energy. However, it is not stretching or compressing a spring, and so there is no spring potential energy.
Can this problem be worked using kinematics?
It is true that you are asked to describe motion in this problem. You also have information about the cause of the motion. So you could work it as a multi-part problem, using force to find acceleration to find velocity of the ball as it leaves the toy, and then use kinematics to find the height. (Note that spring force is not constant and so the process of going from force to acceleration to velocity of the ball as it leaves the toy would most easily take you back to the energy approach.) If you initially recognize that you have the information to work the problem with energy, you can solve it in a single step.
-
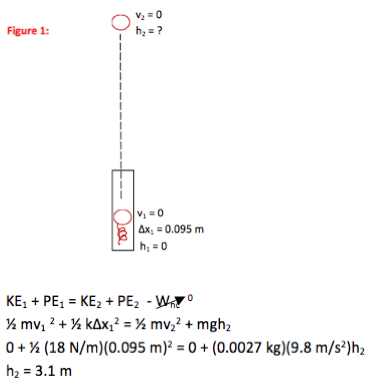
In this problem, you are asked to find how high a ping pong ball rises when it is shot off of a spring. The energy conversion chain for this motion is
spring potential energy→kinetic energy→kinetic energy + gravitational potential energy→gravitational potential energy
Because essentially no energy is lost from the system (air resistance is negligible,) the amount of energy in the system remains constant throughout. This means energy can be compared at any two points. In this case, we are given information about the energy at the starting point and are asked for information about the top of the motion. In other words,
spring potential energystart = gravitational potential energytop
or
½ kΔx12 = mgh2
as seen in the equation above (fill in 0 for both velocities.) The ball rises to a height at which all of the energy in the system (initially from the spring) has been converted to gravitational potential energy.
There are many description of motion problems which can be solved by either kinematics or energy. Energy is almost always the most efficient way to approach these problems as long as enough information is given. (Energy does not require dividing vectors into components, or doing Second Law problems to find acceleration.) In this case, the changing position of the ball reflected a change in the energy of the system, we are not asked to find time, and there are no significant unknown energy losses from the system. Therefore, we are able to approach this question by tracking the energy.