A 0.14 kg baseball is pitched with a speed of 39 m/s. If the batter bunts the ball so that it returns toward the pitcher with a speed of 13 m/s, what is the velocity of the bat immediately after the bunt? Treat this as a one-dimensional problem with the bat allowed to move freely during impact. The mass of the bat is 0.87 kg.
-
In this problem, you are asked to find the velocity of a bat immediately after impact (collision) with a ball. Any time you are asked to find speed or velocity of an object just before or just after a collision or separation, you should check to see if you can use Conservation of Momentum to solve the problem.
In this case, the force of impact between the bat and the ball is much larger than any other forces that act on that system. (The problem hinted at this when it told you to treat the bat as moving freely.) You can, indeed, use Conservation of Momentum.
-
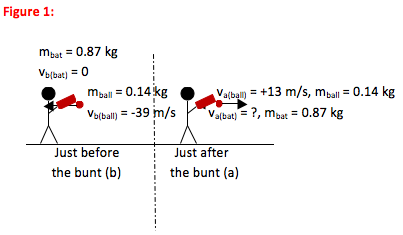
For Conservation of Momentum problems, always draw a picture of the system immediately before the collision or separation and another picture immediately after. Because momentum depends on mass and velocity, label all mass and velocity information
-

Pb = Pa
Any time you understand the motion of a system for which Fextermal Δt≈0, you begin with the Conservation of Momentum equation. -
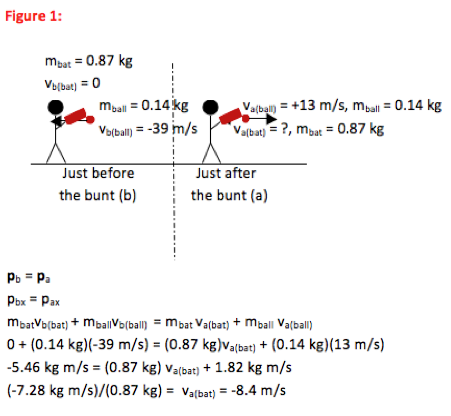
Immediately after the ball is bunted, the bat moves backwards with a velocity of 8.4 m/s towards the batter. No further mathematical solution is needed for this problem.
The problem states that the basketball player throws the ball—in other words, the “player-ball” system separates into two pieces. This is a candidate for a Conservation of Momentum problem.
Because the problem only asks for recoil velocity, you know you only need to consider the effects of the force of the throw—an internal force. So the conditions for using Conservation of Momentum are met.Collisions or separations do not need to be dramatic. You can use Conservation of Momentum on any collision/separation problem in which Fextermal Δt≈0 over the time of the interaction. In other words, the internal force of interaction just needs to be significantly larger than the external forces on the system.
Momentum is conserved on a system only when the net force on that system is small enough that Fextermal Δt is essentially zero. (This comes straight from Newton’s Second Law and the definition of acceleration.) In the case of a collision or separation, the force between the interacting objects or pieces is quite large. So the momentum of each individual object changes because of the force between them. (In this case, the velocity of the baseball and the velocity of the bat each change on impact.) But the net effect of the internal force on the two object system is zero (think of Newton’s Third Law.)
In this case, the force of impact is much larger than other forces present, so you only need to consider the impact force—an internal force. The conditions for using Conservation of Momentum are met.When a batter bunts a ball, he or she holds the bat still and allows the ball to strike the bat.
After the baseball is bunted, it returns toward the pitcher—in other words, it changes direction. Momentum and velocity are vectors, so before and after velocities of the ball must be given opposite signs.
The problem tells us to treat this motion in one dimension. I drew the motion of the baseball to be horizontal, but you would work the problem the same way if you drew it at an angle. Just pick your x-axis along the direction of motion.
Whenever you have a collision between objects, or a separation of one object into smaller objects, you can probably treat the momentum of that multiple object system as being conserved around the time of the collision/separation. The momentum of each individual object, however, changes. Therefore, you need to treat the objects together as your system.
The reason for this is that momentum is conserved on a system only when the net force on that system is small enough that Fextermal Δt is essentially zero. (This comes straight from Newton’s Second Law and the definition of acceleration.) In the case of a collision or separation, the force between the interacting objects or pieces is quite large. So the momentum of each individual object changes because of the force between them. (In this case, the velocity of the baseball and the velocity of the bat each change when they collide.) But the net effect of the internal force on the two object system is zero (think of Newton’s Third Law.) So if we treat the interacting objects together as a single system, momentum of that larger system only changes by Fextermal Δt, or about zero.
Furthermore, you were told that the bat moves freely during the collision. The player, however, experiences a large force with the ground. So the player acts externally to the bat-ball system—the bat and the ball collide, and the player affects the ultimate motion of the bat just as gravity affects the ultimate motion of the ball.This condition is usually met for collision or separation problems.
Momentum is a vector and so you need to treat components separately. Because the motions considered in this problem are along a single direction, I chose that to be my x- axis.
Even though you treat the bat and the ball together as a single system, they do not move together. Therefore, you need to include a separate momentum term for each before and after the collision.
Also remember that momentum is a vector. For a vector equation, put in the correct sign for values that you know (such as the velocities of the ball) and your answer will then give you the correct sign for the unknown quantity (the velocity of the bat.) "
"
The values before the bunt (b) can be put into the equation directly from your picture.
The values after the bunt (a) can be put into the equation directly from your picture.
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
Can this problem be worked using dynamics?
It is certainly true that both the bat and the ball feel the strength of the force between them equally. So you can use the motion of the baseball to solve for the impact force (in terms of Δt which is unknown) and put it into the Second Law equation for the bat (the time intervals will divide out.) However, the equation that you develop as you do so is just the Conservation of Momentum equation.
Can this problem be worked using Conservation of Energy?
No. In most collisions and separations there is a large amount of energy that leaves the system. In this case, you don’t have any information about the amount of that energy. In other words, Wnc is unknown.
Do the external forces of gravity and by the player prevent me from using Conservation of Momentum?
In this problem, you were very specifically asked about velocity of the bat immediately after impact. It is true the velocity of the ball will change as gravity pulls it down, and the velocity of the bat will change as the player holds on to it. However, the impact between the bat and the ball is much larger than these forces, and so they can be ignored over the time of impact. You are also told to assume that the bat moves freely during impact.
In general when you have a collision within a system, the internal force (of impact) is greater than external forces on the system. Therefore, as long as you compare the point in time immediately before the collision to the point in time immediately after the collision, the impulse by external forces (FextermalΔt) is small enough that you can take momentum to be conserved.
How do you know to pick the bat and ball together as a single system?
The quick answer is that whenever you have a collision between objects, or a separation of one object into smaller objects, you can probably treat the momentum of that multiple object system as being conserved around the time of the collision/separation. The momentum of each individual object, however, changes.
The reason for this is that momentum is conserved on a system only when the net force on that system is small enough that Fextermal Δt is essentially zero. (This comes straight from Newton’s Second Law and the definition of acceleration.) In the case of a collision or separation, the force between the interacting objects or pieces is quite large. So the momentum of each individual object changes because of the force between them. (In this case, the velocity of the baseball and the velocity of the bat each change on impact.) But the net effect of the internal force on the two object system is zero (think of Newton’s Third Law.) So if we treat the interacting objects together as a single system, momentum of that larger system only changes by Fextermal Δt, or about zero. Δt is the time over which the collision or separation takes place.
Why didn’t you treat the batter as part of the system?
In this case, you were told that the bat moves freely during the collision. The player, however, experiences a large force with the ground and does not move freely. So the player acts externally to the bat-ball system, putting a force on the bat which will eventually bring it to a stop.
How do you know vb(bat) = 0?
When a batter bunts a ball, he or she holds the bat still and allows the ball to strike the bat.
Why do you include opposite signs on the velocity terms?
After the baseball is bunted, it returns toward the pitcher—in other words, it changes direction. Momentum and velocity are vectors, so before and after velocities of the ball must be given opposite signs.
Don’t you have to worry about gravity or the force of the player on the bat?
In this problem, you were very specifically asked about velocity of the bat immediately after impact. It is true the velocity of the ball will change as gravity pulls it down, and the velocity of the bat will change as the player holds on to it. However, the impact between the bat and the ball is much larger than these forces, and so they can be ignored over the time of impact. You are also told to assume that the bat moves freely during impact.
In general when you have a collision within a system, the internal force (of impact) is greater than external forces on the system. Therefore, as long as you compare the point in time immediately before the collision to the point in time immediately after the collision, the impulse by external forces (FextermalΔt) is small enough that you can take momentum to be conserved.
How do you know to pick the bat and ball together as a single system?
The quick answer is that whenever you have a collision between objects, or a separation of one object into smaller objects, you can probably treat the momentum of that multiple object system as being conserved around the time of the collision/separation. The momentum of each individual object, however, changes.
The reason for this is that momentum is conserved on a system only when the net force on that system is small enough that Fextermal Δt is essentially zero. (This comes straight from Newton’s Second Law and the definition of acceleration.) In the case of a collision or separation, the force between the interacting objects or pieces is quite large. So the momentum of each individual object changes because of the force between them. (In this case, the velocity of the baseball and the velocity of the bat each change on impact.) But the net effect of the internal force on the two object system is zero (think of Newton’s Third Law.) So if we treat the interacting objects together as a single system, momentum of that larger system only changes by Fextermal Δt, or about zero. Δt is the time over which the collision or separation takes place.
Why didn’t you treat the baseball player as part of the system?
In this case, you were told that the bat moves freely during the collision. The player, however, experiences a large force with the ground and does not move freely. So the player acts externally to the bat-ball system, putting a force on the bat which will eventually bring it to a stop.
Can this problem be worked using dynamics?
It is certainly true that both the bat and the ball feel the strength of the force between them equally. So you can use the motion of the baseball to solve for the impact force (in terms of Δt which is unknown) and put it into the Second Law equation for the bat (the time intervals will divide out.) However, the equation that you develop as you do so is just the Conservation of Momentum equation.
Can this problem be worked using energy?
No. In most collisions and separations there is a large amount of energy that leaves the system. In this case, you don’t have any information about the amount of that energy. In other words, Wnc is unknown.
-
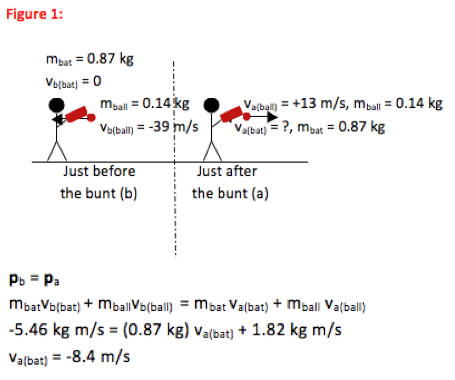
In this problem, you are asked to find velocity of a bat immediately after it was hit with a ball. This is a collision problem and so you should first consider solving it using Conservation of Momentum. Because the force of impact is so much larger than other forces acting on the bat and ball, you are able to ignore any effect of external forces during the time of collision and so conditions to use Conservation of Momentum are, indeed, met.
In this case, over half of the initial kinetic energy of the baseball is lost from the system as heat and sound. (You can find this by calculating the kinetic energies of the bat and ball before and after collision.) So if you were unconvinced earlier that the problem can’t be solved using energy, you can see that now.
Physically, note that the change in momentum of the ball is (0.14 kg)(13 m/s –(-39 m/s)) not (0.14 kg)(39 m/s). In other words, there is a greater change in momentum to reverse direction of an object than to stop it. This should make sense—it hurts more to hit a ball hard enough to send it away from you than it does to stop the ball.
