The driver of an SUV (m = 1700 kg) isn’t paying attention and rear ends a car (m = 950 kg) on level ground at a red light. On impact, both drivers lock their brakes. The SUV and car stick together and travel a distance of 8.2 m before they come to a stop. How fast was the SUV traveling just before the collision? The coefficient of friction between the tires and the road is 0.72.
-
In this problem, you are asked to find the speed of an SUV just before a collision. Any time you are asked to find speed or velocity of an object just before or just after a collision or separation, you should check to see if you can use Conservation of Momentum to solve the problem. Here, you are not given speed information just after the collision. Instead, you are given information about how far the car and SUV travel. So this is not a one-step problem.
If non-conservative forces are either known (as is the case with friction in this problem) or small and if energy is converted from one form to another between the locations, then any time you relate speed and position of an object at two different points conservation of energy is the most direct way to understand the problem.
In this case, you are given stopping force and stopping distance. In other words, you know how much work is done by the non-conservative forces, so you can relate that work to the kinetic energy (and therefore velocity) of the car and SUV just after the collision. In other words, energy is, indeed, the most direct way to learn the velocity of the car and SUV just after the collision.
This, then, is a two part problem. Energy can be tracked from just after the collision until the car and SUV come to a stop. Momentum is conserved during the time of the collision. If you do not recognize both parts of the problem before you begin, that is fine. You can start the problem with either momentum or energy and will quickly find that you need to do an additional problem to find that intermediate velocity.
-
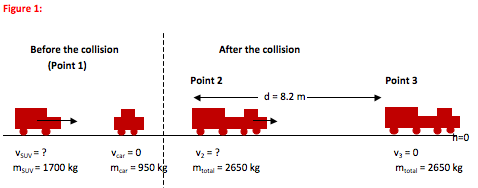
For Conservation of Momentum problems, you always draw a picture of the system immediately before the collision or separation and another picture immediately after (Points 1 and 2.) Because momentum depends on mass and velocity, label all mass and velocity information on the pictures. This helps to avoid mistakes as you fill into the equation later.
For Conservation of Energy problems, you want to show the velocity and position information at all points over which you track energy (Points 2 and 3.)
-

Pb = Pa
Any time you understand the motion of a system for which Fextermal Δt≈0, you begin with the Conservation of Momentum equation.
KE2 + PE2 = KE3 + PE3 – Wnc
Any time you understand the motion of an object by looking at its energy, you begin with the Conservation of Energy equation. This form of the equation works whenever you can track Wnc.
In this problem, we know information about Point 3 and want to learn about Point 1. Therefore, we will begin with the Conservation of Energy equation—we can use information about Point 3 to learn about Point 2. Information about Point 2 is needed to learn about Point 1. -
Step One
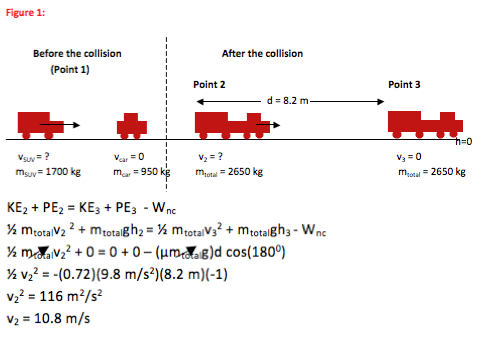
At Point 2, the car/SUV system has enough kinetic energy to travel 8.2 m with the brakes locked. This translates to a speed of 10.8 m/s at Point 2. Continue on to use this information to find the speed of the SUV before the collision.
Step Two
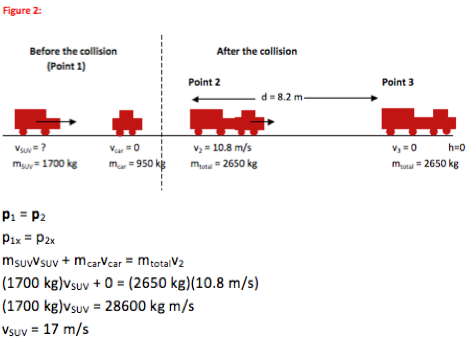
The SUV was traveling at a speed of 17 m/s before the collision. No further mathematical solution is needed for this problem.
Can this problem be worked using dynamics?
It is certainly true that both the SUV and the car feel the strength of the collision force. So you could first use the frictional force to find the acceleration of the car and SUV after the collision and use that acceleration in the kinematics relationships to find their speed immediately after the collision. Then you could use the motion of the car to solve for the average force of the collision (in terms of Δt which is unknown) and put it into the Second Law equation for the SUV (the time intervals will divide out.) However, the equation that you develop as you do so is just the Conservation of Momentum equation.
Why do you have to use Conservation of Momentum? Can’t you just track energy?
In this case, almost 40% of the SUV’s initial kinetic energy leaves the system during the collision as heat and sound energy. Although you can’t know that number until after you solve the problem, you know that whenever objects are deformed, significant work is done by non-conservative forces.
How do you know to pick the SUV and car together as a single system?
It is clear after the collision that the car and SUV behave as a single object. Before the collision, however, they move separately. But remember, whenever you have a collision between objects, or a separation of one object into smaller objects, you can probably treat the momentum of that multiple object system as being conserved around the time of the collision/separation even though the momentum of each individual object changes.
The reason for this is that momentum is conserved on a system only when the net force on that system is small enough that Fextermal Δt is essentially zero. (This comes straight from Newton’s Second Law and the definition of acceleration.) In the case of a collision or separation, the force between the interacting objects or pieces is quite large. So the momentum of each individual object changes because of the force between them. (In this case, the velocity of the SUV goes down and the velocity of the car goes up as a result of the collision.) But the net effect of the internal force on the two object system is zero (think of Newton’s Third Law.) So if we treat the interacting objects together as a single system, momentum of that larger system only changes by Fextermal Δt, or about zero. Δt is the time over which the collision or separation takes place and is small.
Why is 9.8 m/s2 positive?
Work can be either negative or positive, depending on whether the force acts with or against motion. In other words, the sign for Wnc comes from the sign of cosθ. + 9.8 m/s2 is always put in for g.
How did you know which points to compare?
We do not have enough information about the force of the collision to track energy between Points 1 and 2. However, we do know about friction and so can track energy between Points 2 and 3.
What happened to mass?
The car and SUV move together after the collision and so can be treated as a single object with m = (1700 kg + 950 kg) = 2650 kg.
Why do you treat the car and SUV together after the collision?
After the collision, the car and SUV move together. Therefore, I chose to treat them as a single object with a combined mass of 2650 kg. It is equally fine to treat them in two terms—velocity will be the same for both.
Collisions or separations do not need to be dramatic. You can use Conservation of Momentum on any collision/separation problem in which Fextermal Δt≈0 over the time of the interaction. In other words, the internal force of interaction just needs to be significantly larger than the external forces on the system.
Momentum is conserved on a system only when the net force on that system is small enough that Fextermal Δt is essentially zero. (This comes straight from Newton’s Second Law and the definition of acceleration.)
In the case of a collision or separation, the force between the interacting objects or pieces is quite large. So the momentum of each individual object changes because of the force between them. (In this case, the velocity of the SUV and the velocity of the car each change due to the collision force.) But the net effect of the internal force on the two object system is zero (think of Newton’s Third Law.)
In this case, the force of the collision is much larger than any friction on the cars during the collision. So the conditions for using Conservation of Momentum are met.It may not immediately look like energy is the best approach. However, remember that whenever you can track energy you have all the information you need for the Conservation of Energy equation. In this case, knowing friction and distance allow you to find Wnc = Ffrd(cos 1800).
KE = ½ mv2
You do not have any information about the work done by non-conservative forces during the collision, and so you cannot track energy across the collision. You can, however, use Conservation of Momentum.
After the collision has taken place, the cars continue to slow down due to ongoing action of friction. Therefore, momentum is not conserved after the collision but you have enough information to track energy.Once you know you are going to approach the problem using momentum, you know to draw a picture immediately before the collision and another immediately after.
Once you know you are going to approach the problem using momentum, you know to draw a picture immediately before the collision and another immediately after.
In addition, you have planned to track energy from the time of the collision until the cars come to a stop. Therefore, Point 2 will be used in both the energy and the momentum steps of this problem.You are able to track energy from the end of the collision until the car and SUV come to a stop, because you know the non-conservative force on them after the collision.
The car is at a red light, so in the absence of other information it makes sense to assume it is initially at a stop.
After the collision, the SUV and car move together so they can be treated as a single object with the combined mass of (1700 kg + 950 kg) = 2650 kg.
At the end of the problem, the car and SUV have come to a stop—their velocity is zero.
The values for Point 1 can be put into the equation directly from your picture.
The values for Point 2 can be put into the equation directly from your picture.
The values for Point 3 can be put into the equation directly from your picture.
The collision happens over a short enough time interval that the effects of friction are minimal compared to the effects of the collision. In other words, you can ignore friction just during the time of the collision. You cannot use Conservation of Momentum to track speeds for any significant period of time before or after the collision.
Whenever you have a collision between objects, or a separation of one object into smaller objects, you can probably treat the momentum of that multiple object system as being conserved around the time of the collision/separation. The momentum of each individual object, however, changes. Therefore, you need to treat the objects together as your system.
The reason for this is that momentum is conserved on a system only when the net force on that system is small enough that Fextermal Δt is essentially zero. (This comes straight from Newton’s Second Law and the definition of acceleration.) In the case of a collision or separation, the force between the interacting objects or pieces is quite large. So the momentum of each individual object changes because of the force between them. (In this case, the velocity of the car and the velocity of the SUV each change due to the collision.) But the net effect of the internal force on the two object system is zero (think of Newton’s Third Law.) So if we treat the interacting objects together as a single system, momentum of that larger system only changes by Fextermal Δt, or about zero.Between Points 2 and 3, friction is the main non-conservative force on the system and we are given information both about the size of friction and about the distance over which is acts. In other words, we can find Wnc between Points 2 and 3. We do not have information to compute Wnc during the collision because we do not know the size of the collision force.
This condition is usually met during the time of a collision.
Wnc = Fncd cosθ = Ffrictiond cosθ.
We do not have enough information about the force of the collision to track energy between Points 1 and 2. However, we do know about friction and so can track energy between Points 2 and 3.
The car and SUV move together after the collision and so can be treated as a single object with m = (1700 kg + 950 kg) = 2650 kg.
Mass is present in both non-zero terms of the equation, and so it can be divided out. It is equally correct to include it.
Ffriction = µn = µmg as seen by the FBD.
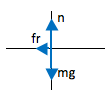
θ is defined as the angle between displacement (to the right in this drawing) and friction (to the left.)
Work can be either negative or positive, depending on whether the force acts with or against motion. In other words, the sign for Wnc comes from the sign of cosθ. + 9.8 m/s2 is always put in for g.
Don’t forget to include the sign that comes from cos(180o) = -1.
The coefficient of friction is 0.72 as given in the problem.
Don’t forget to divide by ½ (multiply by 2.)
Momentum is a vector and so you need to treat components separately. Because the motions considered in this problem are along a single direction, I chose that to be my x- axis.
After the collision has taken place, friction acts over a long enough time that its effects are significant and momentum is not conserved. Therefore, I can only consider Conservation of Momentum over the time of the collision—Point 1 to Point 2.After the collision, the car and SUV move together. Therefore, I chose to treat them as a single object with a combined mass of 2650 kg. It is equally fine to treat them in two terms—velocity will be the same for both.
Before the collision, the car is at a red light. It is reasonable to assume that it is at rest.
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
Why do you have to use Conservation of Momentum? Can’t you just track energy?
In this case, almost 40% of the SUV’s initial kinetic energy leaves the system during the collision as heat and sound energy. Although you can’t know that number until after you solve the problem, you know that whenever objects are deformed, significant work is done by non-conservative forces.
Don’t you have to worry about friction during the collision?
In general when you have a collision within a system, the internal force (of the collision) is greater than external forces (friction) on the system. Therefore, as long as you compare the point in time immediately before the collision to the point in time immediately after the collision, the impulse by external forces (Fextermal Δt) is small enough that you can take momentum to be conserved during the collision.
How do you pick h = 0?
All that matters for describing motion and energy is that you explicitly state where your reference point is. In this case, all action takes place at the same height and so I took that to be h = 0.
How do you know to pick the car and SUV together as a single system?
It is clear after the collision that the car and SUV behave as a single object. Before the collision, however, they move separately. But remember, whenever you have a collision between objects, or a separation of one object into smaller objects, you can probably treat the momentum of that multiple object system as being conserved around the time of the collision/separation even though the momentum of each individual object changes.
The reason for this is that momentum is conserved on a system only when the net force on that system is small enough that Fextermal Δt is essentially zero. (This comes straight from Newton’s Second Law and the definition of acceleration.) In the case of a collision or separation, the force between the interacting objects or pieces is quite large. So the momentum of each individual object changes because of the force between them. (In this case, the velocity of the SUV goes down and the velocity of the car goes up as a result of the collision.) But the net effect of the internal force on the two object system is zero (think of Newton’s Third Law.) So if we treat the interacting objects together as a single system, momentum of that larger system only changes by Fextermal Δt, or about zero. Δt is the time over which the collision or separation takes place and is small.
Can this problem be worked using dynamics?
It is certainly true that both the SUV and the car feel the strength of the collision force. So you could first use the frictional force to find the acceleration of the car and SUV after the collision and use that acceleration in the kinematics relationships to find their speed immediately after the collision. Then you could use the motion of the car to solve for the average force of the collision (in terms of Δt which is unknown) and put it into the Second Law equation for the SUV (the time intervals will divide out.) However, the equation that you develop as you do so is just the Conservation of Momentum equation.
-
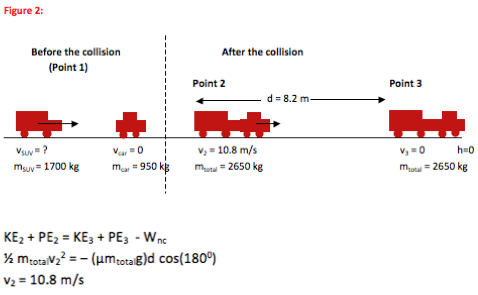
Although the problem asks you to find the speed of the SUV before the collision, you do not have enough information about the speed of the car/SUV system after the collision to begin with Conservation of Momentum. You first need to use distance and speed information to track the energy after the collision to find this velocity.
The energy chain for this motion is kinetic energy→ heat and sound
or
½ mtotalv22 = – Ffrictiond cos(1800)
as seen in the equation above. The speed of 10.8 m/s (25 mph) is reasonable.
Once we know the speed of the car and SUV immediately after the collision (Point 2), we can use that information in the Conservation of Momentum equation to find the speed of the SUV immediately before the collision.
p1 = p2
mSUVvSUV + mcarvcar = mtotalv2
vSUV = 17 m/s
Again, the value of 17 m/s (39 mph) is physically reasonable.
