Two students need to build a Rube Goldberg machine for a middle school Science Olympiad competition. To start the chain of events, they plan to shoot a (2.7 g) ping pong ball horizontally out of a tube using a spring (k = 18 N/m) that has been compressed 6.5 cm. The ping pong ball will strike another ping pong ball that is suspended from a 50. cm long string. The balls will stick together (due to 0.10 g of superglue on the second ball) and swing up to strike a third ball at the top of a ramp. If the top of the ramp is to be just at the top of the swing of the ping pong balls, how high do the students need to build it?
-
In this problem, you are asked to find the height of two ping pong balls after a collision. The question about height suggests that you should use energy, and the collision suggests Conservation of Momentum. So this is not a one-step problem.
If non-conservative forces are either known or small (as is the case in this problem except during the collision) and if energy is converted from one form to another between the locations, then any time you relate speed and position of an object at two different points conservation of energy is the most direct way to understand the problem. In this case, you are given one position (on a spring) and asked for another (height) with a collision in between.
This, then, is a three part problem. Energy is conserved before the collision; momentum is conserved during the collision; energy is conserved after the collision. If you do not recognize all parts of the problem before you begin, that is fine. You can start the problem with either momentum or energy and will quickly find that you need to do additional steps to find the intermediate velocities.
-
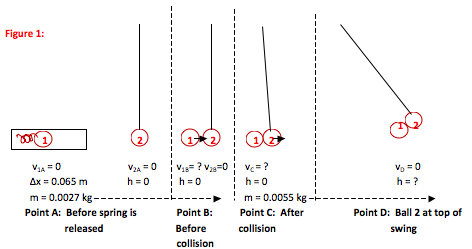
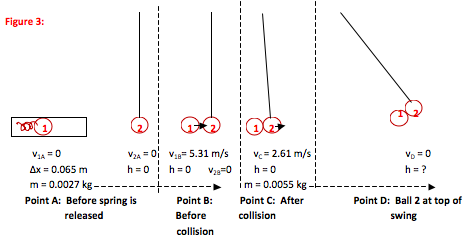
For Conservation of Momentum problems, you always draw a picture of the system immediately before the collision or separation and another picture immediately after (Points B and C.) Because momentum depends on mass and velocity, label all mass and velocity information on the pictures. This helps to avoid mistakes as you fill into the equation later.
For Conservation of Energy problems, you want to show the velocity and position information at all points over which you track energy (Points A to B and Points C to D.)
-

pb = pc
Any time you understand the motion of a system for which Fextermal Δt≈0, you begin with the Conservation of Momentum equation.
KEA + PEA = KEB + PEB – Wnc
KEC + PEC = KED + PED – Wnc
Any time you understand the motion of an object by looking at its energy, you begin with the Conservation of Energy equation. This form of the equation works whenever you can track Wnc.
In this problem, we know information about Point A and want to learn about Point D. Therefore, we will begin with the Conservation of Energy equation—we can use information about Point A to learn about Point B. Information about Point B will provide information about Point C through Conservation of Momentum because we do not know Wnc during that interval. The velocity found for Point C will allow us to learn about height at Point D through Conservation of Energy.
-
Step One
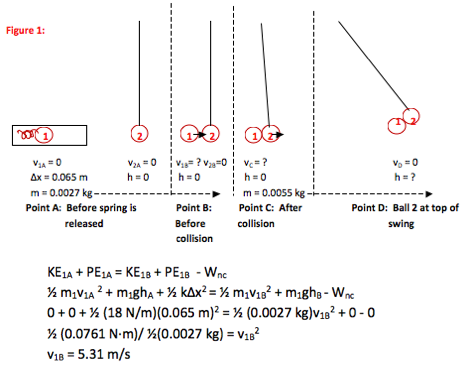
As it leaves the spring, the ping pong ball has a speed of 5.31 m/s. Scroll down to use this information to find the speed of the two ping pong balls just after the collision.
Step Two
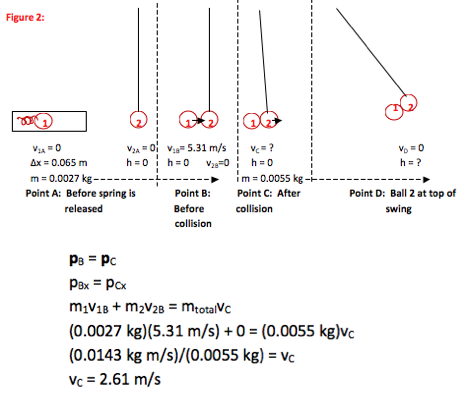
Following the collision, the ping pong balls swing upward with an initial speed of 2.61 m/s. Scroll down to use this information and Conservation of Energy to find out how high they rise.
Step Three
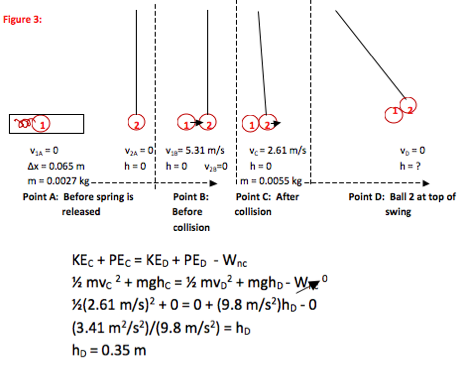
At the top of the swing, the ping pong balls reach a height of 0.35 m, so the ramp needs to be built to 0.35 m above the initial height of the ping pong balls. No further mathematical solution is necessary.
Collisions or separations do not need to be dramatic. You can use Conservation of Momentum on any collision/separation problem in which Fextermal Δt≈0 over the time of the interaction. In other words, the internal force of interaction just needs to be significantly larger than the external forces on the system.
Any time you have an inelastic collision, you know that some energy leaves the system due to the non-conservative force of the collision. In this case, you know that the collision is inelastic because the two ping pong balls stick together.
During the time before the collision, there are no non-conservative forces acting on either ping pong ball. All of the stored potential energy of the spring is transferred to kinetic energy of the ball.
You do not have any information about the work done by non-conservative forces during the collision, and so you cannot track energy across the collision. You can, however, use Conservation of Momentum.
You do not have any information about the work done by non-conservative forces during the collision, and so you cannot track energy across the collision. You can, however, use Conservation of Momentum.
After the collision has taken place, the cars continue to slow down due to ongoing action of friction. Therefore, momentum is not conserved after the collision but you have enough information to track energy.
You are able to track the energy from the ping pong ball resting on the spring until it strikes the second ball because no non-conservative forces act during this time. You need to start with this point, because that is where you have the most information.
Once you know you are going to approach the problem using momentum, you know to draw a picture immediately before the collision and another immediately after.
In addition, you know that energy is conserved up to Point B, and so B will be used in both energy and momentum steps in this problem.Once you know you are going to approach the problem using momentum, you know to draw a picture immediately before the collision and another immediately after.
In addition, you have enough information to track energy from the time of the collision until the ping pong balls come to a stop. Therefore, Point C will be used in both the energy and the momentum steps of this problem.You are able to track energy from the end of the collision until the ping pong balls come to a stop at the top of the swing, because there are no non-conservative forces on them after the collision. You are interested in the final height of the system.
From Point A to Point B, you only need to track the energy of the first ping pong ball. (There are no energy changes for the second during this interval.) Therefore, you only need to consider the mass of that ball. m = (2.7 g)/(1000 g/kg) = 0.0027 kg. It is always easiest to do unit conversions at the “Draw a Picture” stage so that you are fully ready to work the problem.
When the ping pong ball is loaded on the compressed spring, it is at rest (v1A = 0) until the spring is released. Energy is stored in the compression of the spring. Δx = (6.5 cm)/(100 cm/m) = 0.065 m. It is always easiest to do unit conversions at the “Draw a Picture” stage so that you are fully ready to work the problem.
Following the collision, the two ping pong balls and the dot of glue stick together and move as a single object with m = (0.0027 kg + 0.0027 kg + 0.0001 kg) = 0.0055 kg.
At the top of the swing, all of the ping pong balls’ kinetic energy has been converted to gravitational potential energy—the velocity of the balls is zero.
When the two ping pong balls strike into each other, energy leaves the system but momentum is conserved.
Whenever you have a collision between objects, or a separation of one object into smaller objects, you can probably treat the momentum of that multiple object system as being conserved around the time of the collision/separation. The momentum of each individual object, however, changes. Therefore, you need to treat the objects together as your system.
The reason for this is that momentum is conserved on a system only when the net force on that system is small enough that Fextermal Δt is essentially zero. (This comes straight from Newton’s Second Law and the definition of acceleration.) In the case of a collision or separation, the force between the interacting objects or pieces is quite large. So the momentum of each individual object changes because of the force between them. (In this case, the velocity of each ping pong ball changes due to the collision.) But the net effect of the internal force on the two object system is zero (think of Newton’s Third Law.) So if we treat the interacting objects together as a single system, momentum of that larger system only changes by Fextermal Δt, or about zero.Between Points A and B and between Points C and D, there are no significant non-conservative forces. Wnc ≈ 0. So we can use the Conservation of Energy equation.
This condition is usually met during the time of a collision.
The values for Point A can be put into the equation directly from your picture.
The values for Point B can be put into the equation directly from your picture.
The values for Point C can be put into the equation directly from your picture.
The values for Point D can be put into the equation directly from your picture.
We do not have enough information about the force of the collision to track energy across Point B to Point C. However, we do know that there is no non-conservative force acting until the collision. Therefore, we can use what we know about energy at Point A to find the speed of the ball just before the collision (Point B.)
Ping pong ball 1 is at height h = 0 throughout this interval. It is equally fine not to include the mgh term at all since the only potential energy is spring potential energy.
Wnc = 0 because there are no significant forces that take energy out of the system during this period of time.
Initially, the ball is at rest against the spring. It has no kinetic energy at Point A.
At Point A, potential energy is stored in the compression of the spring. The spring is no longer compressed at Point B—there is no spring potential energy at that point.
(N/m)(m2) = N∙m2/m = N∙m
(N∙m)/kg = (kg m/s2)(m)/kg = m2/s2 for the units of v2.
Momentum is a vector and so you need to treat components separately. Because the motions considered in this problem are along a single direction, I chose that to be my x- axis. After the collision has taken place, gravity acts over a long enough time that its effects are significant and momentum is not conserved. Therefore, I can only consider Conservation of Momentum over the time of the collision—Point B to Point C.
After the collision, the two ping pong balls move together. Therefore, I chose to treat them as a single object with a combined mass (including the glue) of 0.0055 kg. This will make the next step (tracking energy of the system) more straightforward.
Before the collision, ping pong ball 2 is at rest—it has no initial momentum.
Because Wnc is zero (there are no non-conservative forces in this interval) and there are no spring potential energy terms, mass of the total system is present in every term. Therefore, it can be divided out.
At the top of the motion, the ping pong balls have come to a stop.
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
We do not have enough information about the force of the collision to track energy across Point B to Point C. However, we do know that there is no non-conservative force acting after the collision. Therefore, we can use what we know about speed at Point C to find information any time after the collision—and we want to know about the top of the swing (or Point D.)
Can this problem be worked using dynamics?
You can certainly use the spring force acting over the compression of the spring to find the velocity of the first ping pong ball as it leaves the spring. However, spring force is not constant and so for that reason if no other it is much more direct to use energy and momentum for this problem.
Why do you have to use Conservation of Momentum? Can’t you just track energy?
In this case, almost half of the ball’s initial energy leaves the system during the collision as heat and sound energy. Although you can’t know that number until after you solve the problem, you know that whenever objects stick together, significant work is done by non-conservative forces.
How do you know to pick the two ping pong balls together as a single system?
It is clear after the collision that the two ping pong balls behave as a single object. Before the collision, however, they move separately. But remember, whenever you have a collision between objects, or a separation of one object into smaller objects, you can probably treat the momentum of that multiple object system as being conserved around the time of the collision/separation even though the momentum of each individual object changes.
The reason for this is that momentum is conserved on a system only when the net force on that system is small enough that Fextermal Δt is essentially zero. (This comes straight from Newton’s Second Law and the definition of acceleration.) In the case of a collision or separation, the force between the interacting objects or pieces is quite large. So the momentum of each individual object changes because of the force between them. (In this case, the velocity of the first ping pong ball goes down and the velocity of the second goes up as a result of the collision.) But the net effect of the internal force on the two object system is zero (think of Newton’s Third Law.) So if we treat the interacting objects together as a single system, momentum of that larger system only changes by Fextermal Δt, or about zero. Δt is the time over which the collision or separation takes place and is small.
How did you know which points to compare?
We do not have enough information about the force of the collision to track energy across Point B to Point C. However, we do know that there is no non-conservative force acting until the collision. Therefore, we can use what we know about energy at Point A to find the speed of the ball just before the collision (Point B.)
Why isn’t there a spring potential energy term at Point B?
At Point A, potential energy is stored in the compression of the spring. The spring is no longer compressed at Point B—there is no spring potential energy at that point.
Why do you treat the ping pong balls as a single object after the collision?
After the collision, the two ping pong balls move together. Therefore, I chose to treat them as a single object with a combined mass (including the glue) of 0.0055 kg. This will make the next step (tracking energy of the system) more straightforward.
How did you know which points to compare?
We do not have enough information about the force of the collision to track energy across Point B to Point C. However, we do know that there is no non-conservative force acting after the collision. Therefore, we can use what we know about speed at Point C to find information any time after the collision—and we want to know about the top of the swing (or Point D.)
What happened to mass?
Because Wnc is zero (there are no non-conservative forces in this interval) and there are no spring potential energy terms, mass of the total system is present in every term. Therefore, it can be divided out.
Why do you have to use Conservation of Momentum? Can’t you just compare the potential energy of the ping pong ball on the spring the potential energy of the ping pong balls at the top of the swing?
In this case, almost half of the ball’s initial energy leaves the system during the collision as heat and sound energy. Although you can’t know that number until after you solve the problem, you know that whenever objects stick together, significant work is done by non-conservative forces.
Don’t you have to worry about gravity during the collision?
In general when you have a collision within a system, the internal force (of the collision) is greater than external forces (gravity, tension) on the system. Therefore, as long as you compare the point in time immediately before the collision to the point in time immediately after the collision, the impulse by external forces (Fextermal Δt) is small enough that you can take momentum to be conserved during the collision.
How do you pick h = 0?
All that matters for describing motion and energy is that you explicitly state where your reference point is. In this case, the ping pong ball leaving the spring strikes the other ball at its lowest point, so I chose that lowest point to be h = 0.
How do you know to pick the two ping pong balls together as a single system?
It is clear after the collision that the two ping pong balls behave as a single object. Before the collision, however, they move separately. But remember, whenever you have a collision between objects, or a separation of one object into smaller objects, you can probably treat the momentum of that multiple object system as being conserved around the time of the collision/separation even though the momentum of each individual object changes.
The reason for this is that momentum is conserved on a system only when the net force on that system is small enough that Fextermal Δt is essentially zero. (This comes straight from Newton’s Second Law and the definition of acceleration.) In the case of a collision or separation, the force between the interacting objects or pieces is quite large. So the momentum of each individual object changes because of the force between them. (In this case, the velocity of the first ping pong ball goes down and the velocity of the second goes up as a result of the collision.) But the net effect of the internal force on the two object system is zero (think of Newton’s Third Law.) So if we treat the interacting objects together as a single system, momentum of that larger system only changes by Fextermal Δt, or about zero. Δt is the time over which the collision or separation takes place and is small.
Can this problem be worked using dynamics and kinematics?
You can certainly use the spring force acting over the compression of the spring to find the velocity of the first ping pong ball as it leaves the spring. However, spring force is not constant and so for that reason if no other it is much more direct to use energy and momentum for this problem.
-
In this problem, you are asked to compare positions of objects with a collision in between. The overall energy chain for the situation is
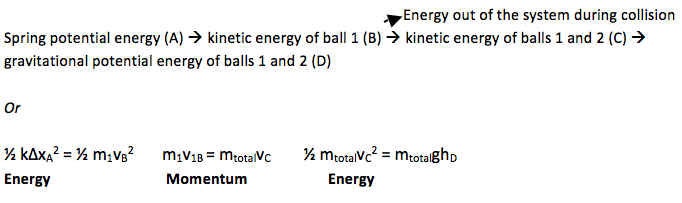
We solved the Conservation of Energy equation from A to B to find the velocity at Point B. Momentum was no conserved because of the force of the spring on the ball.
We solved the Conservation of Momentum equation across the collision (B to C) to find the velocity at Point C. Energy could not be tracked because of the unknown force of the collision.
We again used energy from C to D to arrive at a reasonable value for height of the ramp. Momentum was not conserved because of the action of gravity over this time period.
- Why do you have to use Conservation of Momentum? Can’t you just compare the potential energy of the ping pong ball on the spring the potential energy of the ping pong balls at the top of the swing?
- Don’t you have to worry about gravity during the collision?
- How do you pick h = 0?
- How do you know to pick the two ping pong balls together as a single system?
- Can this problem be worked using dynamics and kinematics?
