A photon with an initial energy of 14 keV scatters off of a free electron and changes direction by 550. What is the wavelength of the scattered photon? What is the recoil speed of the electron?
-
In introduction to quantum mechanics units, you are introduced to a variety of experimental results involving light, atoms, or constituents of atoms. In most cases, when you look at interactions on these tiny scales, you have a foundations of quantum mechanics problem.
In this case, the interaction of interest is that of a photon interacting with a free electron. This is known as the Compton Effect. At root, the Compton Effect is understood through Conservation of Momentum and Conservation of Energy, and so if you recognized this as a momentum problem that shows a good understanding of basic physics applied to a new situation. As always, problems should be initially approached through the core physics concepts regardless of what is requested in the solution.
In quantum mechanics problems, light is sometimes considered as a wave and sometimes as a particle.
protons, neutrons or electrons
-
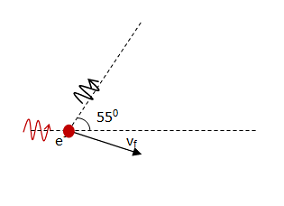
A photon interacting with a free electron can be treated as any other collision in which the interacting objects are free to move. Therefore, the picture looks like that for any other two-dimensional collision problem. There is no need, however, to draw a second picture in which the velocities are divided into components.
How do you know the electron was initially at rest?
I didn’t know for sure. But there was nothing in the problem that indicated any initial motion.
All that matters for this problem is how much the direction of the photon changes—its actual initial direction is not specified and does not matter. I chose it to be in the +x direction for ease of making the sketch. Regardless of your choice for intial direction, the photon after the collision should be traveling 550 from the initial direction of motion (shown by the dotted reference line).
There is no indication in the problem to suggest that the electron was initially in motion and so I took it to be at rest. Following the collision, however, the electron would move in such a way to conserve momentum. Initial momentum is all in the +x direction according to my drawing (py = 0), and so final momentum, too, must not have a y-component. The +y component of the scattered photon’s momentum must be cancelled by a –y component to the electron’s final momentum.
“Scattered photon” merely means that the photon changed direction after its interaction with the electron.
A free electron is not bound in an atom and can therefore absorb any amount of energy. It can be treated as a free particle.
In two dimensional collisions, the motion of the colliding objects before and after the collision needs to be drawn in such a way that directions are clearly shown.
For the Compton Effect, Conservation of Momentum and Conservation of Energy have been combined into a partially solved equation based on the scattering angle of the photon. You will not need to work with x- and y-components of the momentum separately in this problem.
-
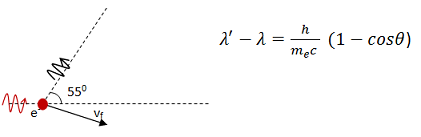
Whenever a photon interacts with a free electron, it is asking you to think about the Compton Effect. Your book has probably provided you with this partially-solved version of the Conservation of Momentumand Conservation of Energy equations as they apply to photon-electron scattering. One caution with partially-solved or situation specific equations: Make sure that you understand both when the equation applies and what each symbol represents.
In this problem, you are asked first for the photon wavelength and then for the electron energy. As always, begin with the core physics behind the problem and let that understanding lead you to the answer to secondary questions. You do not need to picture the full solution before you begin.
The derivation of the Compton Effect equation from momentum and energy is straightforward but too long to reproduce here. A quick internet search will bring up multiple sites showing the derivation if your book does not include it.
λ in this case represents the wavelength of the photon. The ‘ indicates the wavelength after the photon has interacted with the electron.
Remember this equation comes from energy and momentum transfer between the photon and the electron. me is the mass of the electron.
θ represents the angle between the original motion of the photon and its final direction of motion.
The Compton Effect equation applies only to the situation in which a photon interacts with/scatters off a free electron. It comes from solving the Conservation of Momentum and Conservation of Energy equations for an elastic collision between a photon and an electron. Note also that the expression for photon energy (E = hf = hc/λ) was used in the derivation.
-
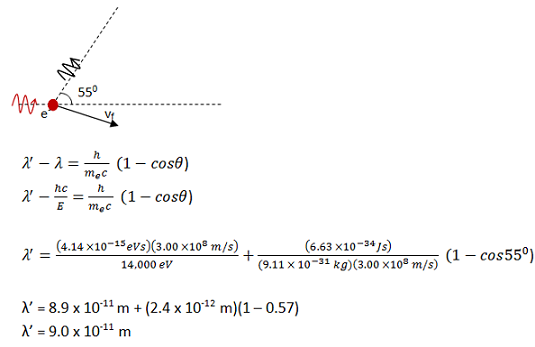
The Compton Effect equation directly gives the wavelength of the scattered photon. Scroll down in order to find the final speed of the electron.
I don’t know the initial wavelength of the photon. How do I begin?
For a photon, E = hf. By the wave equation (c = fλ), E = hc/λ. Multiply by λ and divide by E to get λ = hc/E.
What is an eV?
An eV (electron volt) is the unit of energy given to one electron that has been accelerated through a potential difference of 1 Volt. It is equal to 1.6 x 10-19 J. Because the value for photon energy was given in keV (1 keV = 1000 eV), I made sure to use Planck’s Constant (h) also in eV in this term.
Why did you use two different values for h?
In the first term, energy was given in keV so I used h in eV s. In the second term, electron mass and the speed of light were used in MKS units and so I needed to also use h in MKS units.
An eV (electron volt) is the unit of energy given to one electron that has been accelerated through a potential difference of 1 Volt. It is equal to 1.6 x 10-19 J. Because the value for photon energy was given in keV (1 keV = 1000 eV), I made sure to use Planck’s Constant (h) also in eV in this term.
For a photon, E = hf. By the wave equation (c = fλ), E = hc/λ. Multiply by λ and divide by E to get λ = hc/E.
c in this case stands for the speed of light.
If you use electron mass in kg, you must work with Planck’s constant also in MKS units.
Two significant figures were given in the information used for this problem, so two significant figures are included in the solution.
----------------------------------------------------------------------------------------------
Step 2
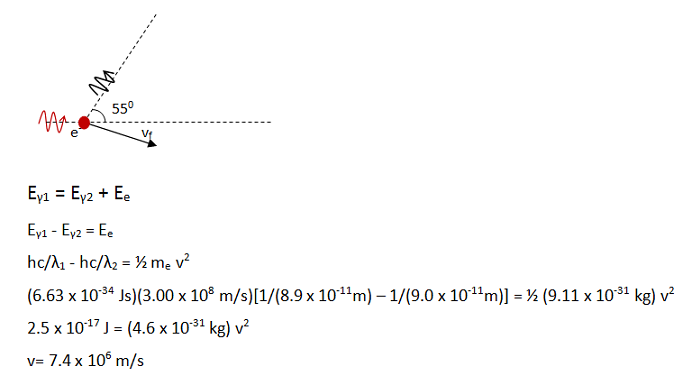
In the second question, you are asked to find the speed of the electron after the interaction with the photon. As has been discussed throughout this problem, the Compton Effect reflects a conservation of energy and momentum between the electron and the photon. It is always easier to use energy than momentum if you can, and so I began by tracking what happened to the initial energy of the photon. No further solution in necessary in this problem.
In this case, the part of the initial energy of the photon stayed with the photon—you are told that it scatters off the electron and changes direction. The rest of the energy goes into recoil velocity (kinetic energy) of the electron.
For a photon, E = hf. By the wave equation (c = fλ), E = hc/λ.
The energy given to the electron is kinetic energy. KE = ½ mv2.
Because this part of the problem is worked with MKS units, make sure to use h in MKS units also.
Energy in the universe is always conserved. If you have enough information in a problem to track what happens to the energy, it is typically the easiest and most powerful way to approach a problem. In this case, you have the additional motivation that momentum is a vector. Even though it, too, is conserved in this case, scalar math is always easier than vector math.
-

Once you recognize this problem as the Compton Effect, you can answer the first question mathematically merely by plugging into* the Compton equation. However, to understand the problem you need to recognize that this equation tracks momentum and energy.
Remember that in order to understand the experimental results of the Compton Effect, we treat light as both a particle rather and as a wave. In other words, we understand the interaction of light with the electron as an elastic collision between a photon (light particle) and the electron. In this interaction, the photon gives some of its energy to the electron. In understanding light as a wave, however, we recognize that lower energy light has a longer wavelength (as given by E = hf = hc/λ) than high energy light. This is in agreement with the experimental results that show the scattered light has a longer wavelength than the incident light.
*Note that the energy of a photon is related to its wavelength and so the definition of photon energy was also used in order to relate the given quantities to those used in the equation.
What is the difference between an electron and a free electron? Why does it matter?
If an electron is bound in an atom, its energy is quantized—it can only have certain energy values (those of the orbitals.) A free electron can have any energy. This matters in photon collisions, because an electron in an atom can only absorb photon energy if it is of just the right amount to take it to another orbital. A free electron can interact with a photon of any energy and absorb all or part of that energy—collisions of free electrons and photons can be treated just like other collisions.
What do you mean by “scatters”?
This just means that the photon changes direction as it interacts with the electron. Its energy is not fully absorbed by the electron.
