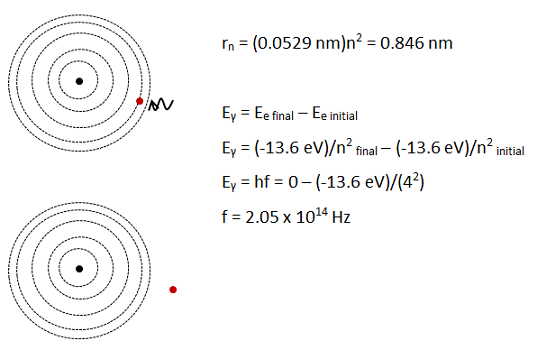
According to the Bohr model of the atom, what is the radius of orbit of an electron in the n=4 orbital of hydrogen? What minimum frequency photon is required to remove the electron from the atom?
-
In introduction to quantum mechanics units, you are introduced to a variety of experimental results involving light, atoms, or constituents of atoms. In most cases, when you look at interactions on these tiny scales, you have a foundations of quantum mechanics problem.
In this case, you are explicitly asked about the Bohr model of the atom. You have equations that give the radius and energy of each orbit in the Bohr atom, and so this is essentially a one-step or definition problem. If you also recognize the energy conservation component of this problem (photon energy is given to the electron) from the beginning, that is good! But don’t worry if you don’t see all parts at the start of the problem—you will be led to conservation of energy as you progress.
In quantum mechanics problems, light is sometimes considered as a wave and sometimes as a particle.
protons, neutrons or electrons
The Bohr model of the atom treats the electron as a particle orbiting the central nucleus in one of the allowed circular orbits. The radii of orbits and allowed energy levels of the electron come from treating angular momentum as being quantized. Bohr was able to replicate observations by taking angular momentum values to be integer multiples of h/2π and using Newton’s Laws and Conservation of Energy.
-
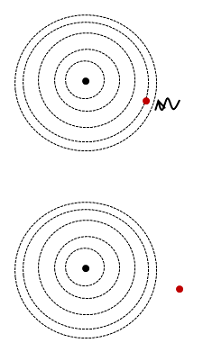
As for most definition problems, a picture is not required to organize the information. However, it may help you to picture the energy transfer.
Why did you draw five orbits for the electron?
I chose the number of orbits to draw randomly. I knew that I needed to show at least four orbits because the electron is in the 4th, and wanted to show at least one more. You can include as many more as you like. Note that the energy difference between the nth and nth + 1 orbit gets smaller and smaller as n approaches infinity.
Orbits in the Bohr model are taken to be circles, each numbered according to its distance from the nucleus. The inner most orbit is the n=1 orbit, the next is n=2, etc.
Photons are typically drawn with wavy lines. In this case, the photon is coming in to the atom and absorbed by the electron.
Remember that photons are energy. In this situation, photon energy is absorbed by the electron in order to free it. In other words, it goes to increasing the electric potential energy of the electron.
-
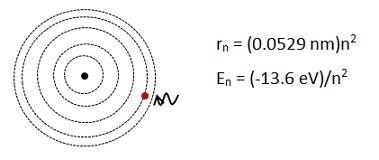
Whenever you are asked about the Bohr model of the atom, begin by checking to see if you have a definition equation for the quantity(s) that you want to understand. In this case, both radius and energy for each orbital are given directly through the above equations. If at this stage you also recognize that you will need to know the energy of a photon (E = hf), that is great. If not, you will come to it as you work the problem.
These are not the equations given in my text. Where did you get the numbers?
The numbers in these equations are just the solved combination of constants that are given in some books.
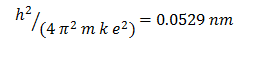
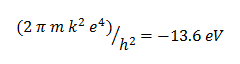
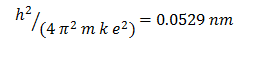
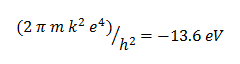
Note that the – sign in this equation reflects the choice of 0 for electric potential energy. For a free electron, n is infinity and energy is 0. For any orbital less than infinity, the electron is in a bound state and the (electric potential) energy is negative.
n in this case just numbers each orbital. n=1 for the first orbit, n=2 for the second, etc.
-
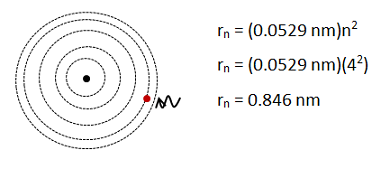
The radius of the nth orbital is given directly by this equation. Scroll down to solve for the minimum frequency of the photon.
Remember, n just numbers the orbitals.
The constants in the equation were calculated to three significant figures. “4” in this case is an exact number—we are counting orbitals so it is known exactly—and so the answer is given in three significant figures.
----------------------------------------------------------------------------------------------
Step 2
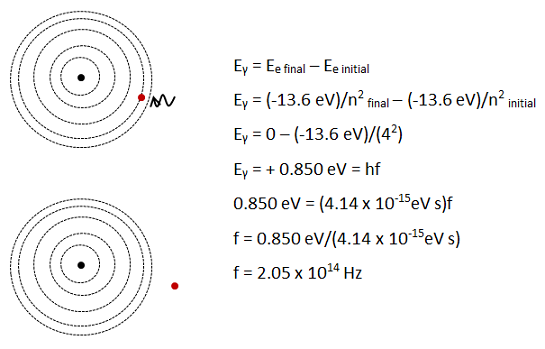
In the second question, the electron is freed from the atom due to interaction with the photon. If you did not previously recognize this as an energy problem, at this stage the fact that you know energy levels of the Bohr atom should suggest to you that you can track energy.
How did you know to treat this as an energy problem?
The best way to recognize that this is an energy question is to recognize that in order to free and electron from an atom you must put energy into the system. So the key physics is energy as reflected in the first line of the solution. You can then use your definitions of photon energy and energy levels in the Bohr atom to relate energy to the information of the problem.
In this case, the energy of the photon is given to the electron. Remember that energy of a photon is given by hf.
Einitial = Efinal
Eγ + E e initial = Ee final
Eγ = Ee final - E e initial
The energy of a free, or unbound, electron can be calculated by taking it to be in the n=infinity orbital. 1 divided by infinity is zero. Alternately, you might remember that we have chosen the zero point of electric potential energy to be 0 when the electron is free.
Note that the + sign correctly reflects that fact that you need to put energy into the system in order to free the electron.
Because the expression for the energy in a Bohr atom is given in eV, make sure also calculate the energy of the photon in eV.
The constants in the Bohr energy equation were calculated to three significant figures. “4” in this case is an exact number—we are counting orbitals so it is known exactly—and so the answer is given in three significant figures.
A better reason to recognize that this is an energy question is to recognize that in order to free and electron from an atom you must put energy into the system. So the key physics is energy as reflected in the first line of the solution. You can then use your definitions of photon energy and energy levels in the Bohr atom to relate energy to the information of the problem.
-
The first part of this problem is merely a one-step problem describing the Bohr atom.
For the second question, you need to recognize that energy must be put into the system in order to free the electron. Just as for Conservation of Energy problems involving mechanical energy, it does not matter what is given and what you are asked to find. Always begin the the core physics of the situation.
What is the Bohr model?
The Bohr model of the atom treats the electron as a particle orbiting the central nucleus in one of the allowed circular orbits. The radii of orbits and allowed energy levels of the electron come from treating angular momentum as being quantized. Bohr was able to replicate observations by taking angular momentum values to be integer multiples of h/2π and using Newton’s Laws and Conservation of Energy.
How do you relate photon frequency to the Bohr model?
As always, don’t worry if you don’t see the full approach to the problem when you start! Begin with what you understand. In this case, as you explore the Bohr model you will see that you know about the energy of the electron and so ultimately you will track energy from the photon to the electron.
