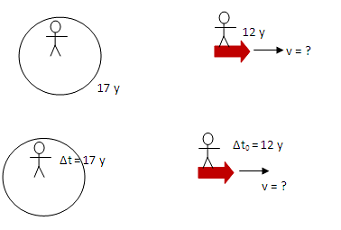
An astronaut on a spaceship traveling at a constant velocity away from Earth travels for 12 years before she encounters another solar system. According to her colleagues on Earth, the trip to the new solar system took 17 years. How fast did the astronaut travel? How far from Earth is the new solar system?
-
In this problem, an observer on the spaceship measures how long it takes her to make a trip, and an observer on the Earth times the same trip. Any problem that relates the measurements of two observers measuring the same thing is a relativity problem.
In the second question, you are asked to relate distance to the closely related quantities of speed and time. The second question is just a definition.
-
How do you know which way the spaceship moves?
It doesn’t matter whether you drew the Earth on the right or the left side of the page. All that is important is that the ship moves relative to Earth in a line along the length of the ship. You only solve for speed (not direction) in this problem so all work will be the same.
It doesn’t matter whether you drew the Earth on the right or the left side of the page. All that is important is that the ship moves relative to Earth in a line along the length of the ship. You only solve for speed (not direction) in this problem so all work will be the same.
In this problem, both observers are timing how long it takes the astronaut on the ship to make a trip. Therefore, the frame of the astronaut on the spaceship is the proper frame. As always, the system of interest is identified in red.
Make sure to show all measurements on your drawing. To begin, just put each measurement down next to the observer who measured it. You will assign labels to the variables as a second step.
One of the most important things to do in Special Relativity problems is to clearly and correctly identify the reference frames of the observers. In this problem, the observers were clearly stated—an astronaut on the ship and her colleagues on Earth—and so figures to represent the observers should be drawn on the ship and on the Earth.
To identify which of these observers is in the proper frame, ask what is being measured. In this case, it is time for the astronaut to make the trip and so the spaceship (and the astronaut on it) is in the proper frame. The subscript 0 on a measurement indicates it was made in the proper frame.
-
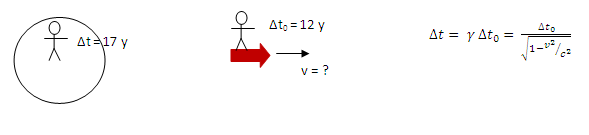
In this case, both observers measure the time it takes the astronaut and spaceship to travel, and so the problem is understood through the relativistic time equation regardless of what quantity is requested in the solution.
-
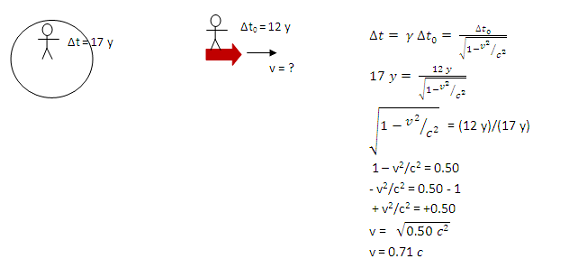
The spaceship is traveling at 73% the speed of light (or 2.2 x 108 m/s) away from Earth. No further mathematical solution is needed in this problem.
Why isn't the final answer in m/s?
It is convenient to solve for speeds in terms of the speed of light. If you desire an answer in terms of m/s, just substitute 3.00 x 108 m/s in for c
In this step, I multiplied each side by √(1-v2⁄c2) and divided each side by 17 y.
In this step, I divided 12 y by 17 y to get 0.71 (the units cancel) and then squared each side of the equation.
In this step, I not only subtracted but also multiplied both sides by -1 in order to get rid of the – sign in front of the v2 term.
In order to solve for v, I need to get it alone on one side. In this step, I multiplied each side by c2 and then took the square root of both sides.
It is convenient to solve for speeds in terms of the speed of light. If you desire an answer in terms of m/s, just substitute 3.00 x 108 m/s in for c
----------------------------------------------------------------------------------------------
Step 2
Now that you know how fast the spaceship is traveling, it is only a definition problem to determine how far it goes.
Two cautions:
- Because you want distance in conventional units such as meters, make sure to use velocity in units of m/s and not in units of c.
- With the exception of the three relativistic equations, all physics equations are worked within a single reference frame. Make sure to use distance and time measurements within the same frame in the velocity equation.
The definition of velocity is

The new solar system is 1.1 x 1017 m from Earth. No further mathematical solution is needed in this problem.
-
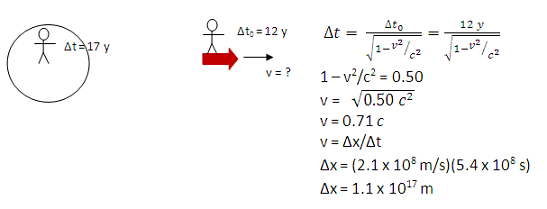
Regardless of what you were asked to find, this is a relativistic time problem because two observers in different reference frames both time the same event. In this case, it is the astronaut on the spaceship that does the action being timed, and so the spaceship is the proper frame (and measures the shorter time.)
Because the two measurements are noticeably different from each other, you expect that the relative speed of the frames should be a substantial fraction of the speed of light as found.
In the second question, you were asked to related length to time. This is not a relativistic question because it does not involve two observers measuring the same thing. Rather a single observer measured two different things. All physics equations that related different quantities must be worked in a single reference frame.
------------------------------------------------------------------------------------------Note that if you wanted to know the distance as measured by the astronaut, you could either use her time measurement in the velocity definition equation or you could use the relativistic length equation to relate her measurement of distance to that of her colleagues back on Earth.
The relative speed of the two reference frames is a variable in all of the relativistic equations and so it is not a useful criterion for selecting the equation to use. You should always base your choice on the measurement that is compared by the two observers.
No reference frame is explicitly stated for the distance in this problem. Because you want the distance between Earth and the new solar system, it makes sense to assume the requested distance is that as measured in the frame of the Earth.
(17 y)(365.25 days/y)(24 hr/day)(3600 s/hr) = 5.4 x 108 s
Two significant figures were given in the information of this problem, so two significant figures are included in the solution.
How can I start this problem? All of the relativity equations use velocity.
It doesn’t matter what was given or requested—you always work problems according to the key physics involved. In this case, two observers both measure the time it takes to make a trip, and so this is a relativistic time problem.