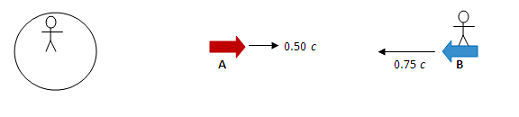
An observer on Earth watches two spaceships. According to his measurements, spaceship A is traveling away from Earth at half the speed of light, and spaceship B is approaching Earth at 0.75 c. How fast is spaceship A moving according to the crew on spaceship B?
-
In this problem, an observer on Earth and an observer on spaceship B both measure the speed of spaceship A. Any problem that relates the measurements of two observers measuring the same thing is a relativity problem.
-
How do you know which way the spaceship moves?
It doesn’t matter whether you drew the Earth on the right or the left side of the page. All that is important is the relative motion (towards or away from Earth.) The statement of this problem does not make it clear as to whether or not the ships are on the same or opposite sides of the Earth. If you interpreted the description to mean that the two spacecraft are on different sides of the Earth, you should show both ships moving in the same direction and will get a different numerical answer. The approach that you use will be the same.
How did you know to pick spaceship A as the system?
Both the observer on Earth and the crew on spaceship B measure the speed of spaceship A. Therefore, spaceship A is the system being studied.
Why don't you show the proper frame?
There is no proper frame for velocity addition problems. This will be discussed further in the “Solve” step of the problem.
All relativity problems relate the observations made by two observers. In this case, the problem explicitly states that there is an observer on Earth. Include a sketch of this observer on the figure!
Both the observer on Earth and the crew on spaceship B measure the speed of spaceship A. Therefore, spaceship A is the system being studied.
It is important to show the velocities on the figure, with arrows to indicate their directions. (The figure is a picture of all the information that you have, in a format that can be directly transferred in the appropriate mathematical relationship.) However, at this point do not assign symbols to the velocities. You will need to determine which frame is which before you can do that. Proceed to the next two steps to see how the symbols should be assigned.
All relativity problems relate the observations made by two observers. In this case, the problem explicitly asks for a measurement made by the crew on spaceship B. Therefore, sketch that observer (the crew) on spaceship B.
-
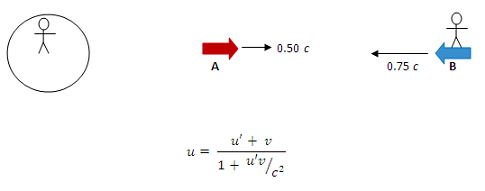
In this case, both observers measure the speed of spaceship A. Therefore, this is a relativistic velocity addition problem regardless of what quantity is requested in the solution.
How do I know which velocity is u, which is u', and which is v?
There are three different speeds to track in velocity addition problems: the speed of the system according to one observer, the speed of the system according to the other observer, and the relative speed of the observers. There is some logic to the way that the variables are named.
u and u’ are the speed of the system according to the observer in the unprime frame and the observer in the prime frame, respectively. Note that “u” is used for both, since they are the speed of the same thing.
v is a different symbol, so it is the speed of something other than the system represented by u—it is the relative speed of the two observers. Because it does not have a prime, it is the relative speed as measured by the observer in the unprime frame.
All three special relativity equations involve velocity or speed. Therefore, it is not useful to use the quantity requested in the question as a criterion for selecting the relation. In this problem, both observers measure the speed of some third object. In other words, the measurement being compared by the observers is speed. The measurement being compared by the observers is the criterion on which the relation should be selected.
There are three different speeds to track in velocity addition problems: the speed of the system according to one observer, the speed of the system according to the other observer, and the relative speed of the observers. There is some logic to the way that the variables are named.
u and u’ are the speed of the system according to the observer in the unprime frame and the observer in the prime frame, respectively. Note that “u” is used for both, since they are the speed of the same thing.
v is a different symbol, so it is the speed of something other than the system represented by u—it is the relative speed of the two observers. Because it does not have a prime, it is the relative speed as measured by the observer in the unprime frame.
-
Step 1
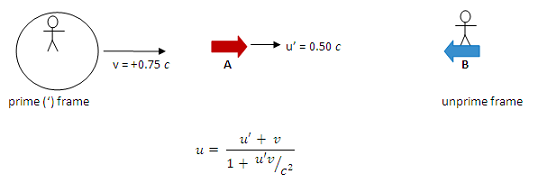
The first step in solving a velocity addition problem is to identify which is the prime observer and which is the unprime observer. There is no proper frame, so the choice is yours! However, the math is always easier if u (rather than u’) is the unknown quantity. Once the prime and unprime frame are identified, symbols can be assigned to the given quantities.
What happened to the velocity arrow on spaceship B?
Once you have assigned the prime and unprime frames, you can assign symbols to the quantities that are given. Because 0.75 c is the relative speed of the observers, it is given the symbol v. Because v does not have a ', you must assign it as the speed of the ' observer (Earth) according to the observer in the unprime frame (spaceship B). Therefore, 0.75 c is the Earth’s motion according to someone on B. The Earth and B are moving toward each other, which is the + direction for Earth as shown in this figure.
Math is easiest if the prime (') frame is that of the observer whose measurement you know. You are given the speed of the system according to the observer on Earth, so it is easiest if Earth is the ' frame.
Math is easiest if the prime (') frame is that of the observer whose measurement you know, and the unprime frame that of the observer whose measurement you want to find. You want to find the speed of the system according to the crew on spaceship B, so it is easiest if spaceship B is the unprime frame.
Once you have assigned the prime and unprime frames, you can assign symbols to the quantities that are given. Because 0.50 c is the speed of the system, it is given the symbol u. Because it is the speed of the system according to the observer in the prime frame, it is also given a '. Therefore, 0.50 c is identified as u’. Also note that it is in the positive direction.
Once you have assigned the prime and unprime frames, you can assign symbols to the quantities that are given. Because 0.75 c is the relative speed of the observers, it is given the symbol v. Because v does not have a ', you must assign it as the speed of the ' observer (Earth) according to the observer in the unprime frame (spaceship B). Therefore, 0.75 c is identified as v and must be given as the sign of Earth’s motion according to someone on B. The Earth and B are moving toward each other, which is the + direction for Earth as shown in this figure.
----------------------------------------------------------------------------------------------
Step 2
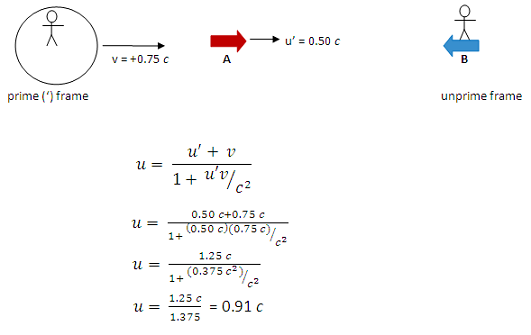
According to an observer on spaceship B, spaceship A approaches with a speed of 0.91 c. No further mathematical solution is necessary.
Make sure to note that there is a factor of c in both u’ and v. Therefore, the c2 in the denominator cancels out.
Two significant figures were given in the information of this problem, so two significant figures are included in the solution.
-
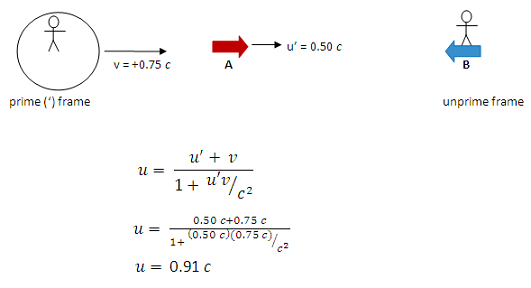
Regardless of what you were asked to find, this is a relativistic velocity problem because two observers in different reference frames both measure the speed of the same thing. There is no proper frame in this situation, so the prime and unprime frames for the observers need to be chosen and clearly identified.
The numerical answer makes sense. First, we know that velocity will never be greater than c. Second, because spaceships A and B are approaching each other, we expect that the speed of A relative to B will be greater than the speed of either of the spaceships as measured by an observer on Earth.
How can I start this problem? All of the relativity equations use velocity.
It doesn’t matter what was given or requested—you always work problems according to the key physics involved. In this case, two observers both measure the speed of a third object (spaceship A), and so this is a relativistic velocity addition problem.