An astronaut on a spaceship approaching Earth observes that it takes 2.0 hours for an asteroid to pass out of sight. Mission control on Earth measures the transit time of the asteroiod to be 25% longer than that. A second spaceship approaches Earth from the other side at one third the speed of the first spaceship. What is the transit time of the asteroid as measured on the second ship?
-
In this problem, two observers on different spaceships (plus an observer on Earth) measure the time it takes an asteroid to cover a certain path. Any problem that relates the measurements of two observers measuring the same thing is a relativity problem.
You may feel uncomfortable by the lack of numbers in the problem. It is certainly true, for example, that you will need to know the velocities of the spaceships in order to calculate the time interval. In other words, this is a multi-part problem. Don't worry if you don't see all parts of a problem at the beginning. Start with the key physics concept, relativity, and work smaller problems as you need them.
When you work relativity problems, you will always compare the observations made by two observers. In this problem, you know of three observers but can only work with two at a time.
Is this a time dilation or velocity addition problem?
In this case, it is actually both. However, don't worry if you don't see that at this point. Draw a picture to organize your basic information-you can draw additional pictures later as the problem unfolds.
-
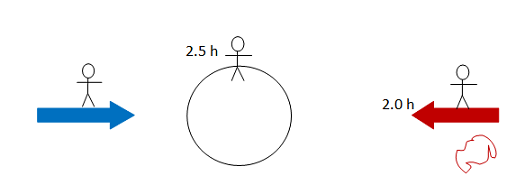
For relativity problems, a useful picture shows the location of the observers and any other information. It is not a good idea to put labels on the information when you first draw the picture. Wait until you determine the proper and/or prime frame so that you can lable the quantities correctly.
The time interval as measured on Earth is 25% more, or 1.25 x, as long as that measured on the spaceship. (1.25)(2.0 h) = 2.5 h
It doesn't matter which side you drew which spaceship. As long as they are on opposite sides of the Earth, both going towards the Earth, you are fine. If you reversed the pictures, your signs for direction will be opposite mine but the numerical values will be the same.
For time dilation and length contraction problems you need to identify the proper frame. For velocity addition problems, you need to select a prime frame. You may have thought ahead enough to know that in this case you will work both kinds of problems. But remember, you only work one at a time. So you will use proper frame for the time dilation sub-problems, and prime frame for the velocity addition sub-problem.
This is a difficult problem to initially determine the system of interest. It is really the time interval as measured by the astronaut on the ship that forms the focus of this problem, as shown by the red shading of the spaceship. However, if you identified the asteroid (whose motion is being timed) as the system of interest that is ok, too, and it should lead you to the same mathematical work.
-
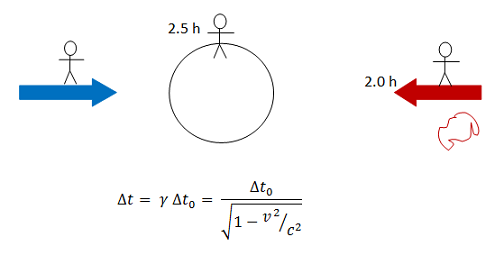
In this case, the observers on the two spaceships each measure the time of transit of the asteroid so this is a time dilation problem regardless of what information is given. Notice, however, that you need to know the relative speed of the two spaceships in order to calculate the time interval, and so at this point you have to recognize that this is a multi-part problem even if you weren't aware of that before.
Your pre-problem, then, requires that you find the relative speed of the ships. If, rather than comparing the time intervals measured by the two astronauts, you instead compare the time interval measured by one astronaut to that measured by Mission Control, you can use the time dilation equation to find the velocity of that astronaut's ship.
What is v in this equation?
v is the relative speed of the observers in the two reference frames. When you compare measurements made by an astronaut and Mission Control, it is the speed at which the spaceship moves toward Earth. When you compare measurements made by the two astronauts, it is the speed at which the two ships approach each other.
How can I calculate the relative speed between the two spaceships?
This is ultimately going to be a three step problem. You will use time to find the relative speed between the spaceship and Earth, and then can use velocity addition to find the relative speeds between the spaceships.
How did you know to use time dilation to find the velocity of the spaceship?
If you have problems seeing this step, go to the Speed of a Spaceship II example problem. It covers finding relative speed based on two time measurements in full detail.
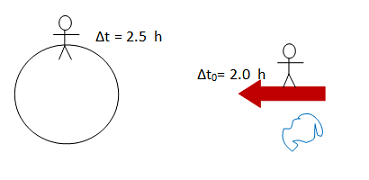
The information given in this problem is the measurements made by two observers (on the first ship and on Earth) about the time of travel of the asteroid. Whenever two observers measure the same time interval, the information is understood through the relativistic time dilation equation. Because both times were given, the information allows you to find the relative motion of the two observers-the speed at which the first ship approaches Earth. If you have problems seeing this step, go to the Speed of a Spaceship II example problem. It covers finding relative speed based on two time measurements in full detail.
v is the relative speed between the observers who measure t and t0. Ultimately you will use the relative speed between the ships to calculate the time interval measured by the astronaut on the second ship. In the first step, you will use the times measured on the first ship and on Earth to learn about the motion of the first ship.
As soon as you know that you will understand a problem through time dilation, you need to identify the proper frame. To identify which of the observers is in the proper frame, ask what is being measured. In this case, the answer is not straightforward. The asteroid's motion is being timed as it moves past the spaceship. If this distinction is too subtle, you can always remember that the proper time is the smallest of the time measurements. With either approach, the spaceship is the proper frame for timing the motion of the asteroid.
-
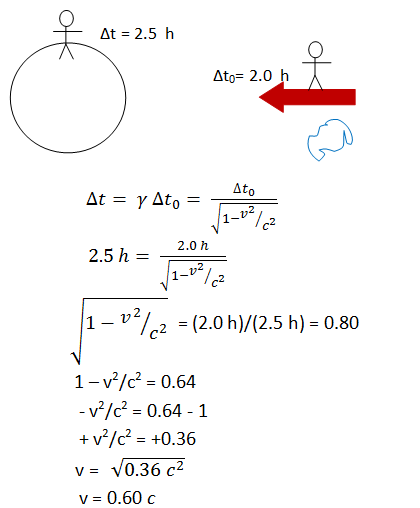
Comparison of time measurements made on the Earth and on the spaceship allows us to find the relative speed of the spaceship and the Earth. We know that the second ship approaches Earth at 1/3 the speed of the first, or (1/3)(0.60 c) =(0.20 c). Scroll down to use this information to find the relative speed between the two spaceships.
Why isn't the final answer in m/s?
It is convenient to solve for speeds in terms of the speed of light. If you desire an answer in terms of m/s, just substitute 3.00 x 108 m/s in for c.
In this step, I multiplied each side by the square root of (1-v2/c2) and divided each side by 2.5 h.
In this step, I not both subtracted and multiplied both sides by -1 in order to get rid of the - sign in front of the v2 term.
In order to solve for v, I need to get it alone on one side. In this step, I multiplied each side by c2 and then took the square root of both sides.
Remember, the goal of the problem is to compare the time interval measurements made on the two spaceships. In order to do that, we need to know the relative speed of the two ships. At this stage, we know the speed of each ship relative to the Earth but not relative to each other.
----------------------------------------------------------------------------------------------
Step 2
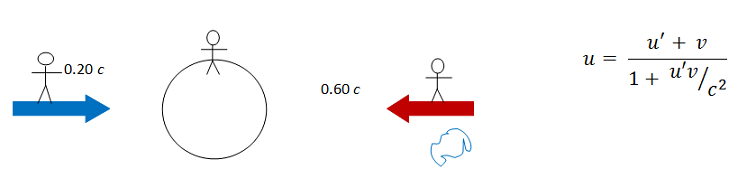
Before you can work with the velocity addition equation, you need to identify who is the prime observer and who is the unprime observer. There is no proper frame, so the choice is yours! However, the math is always easier if u (rather than u') is the unknown quantity.
Once the prime and unprime frame are identified, symbols can be assigned to the given quantities on the figure. If you struggle with this step, go to Speed of a Spaceship III for a more detailed example of finding the relative speed between two reference frames.
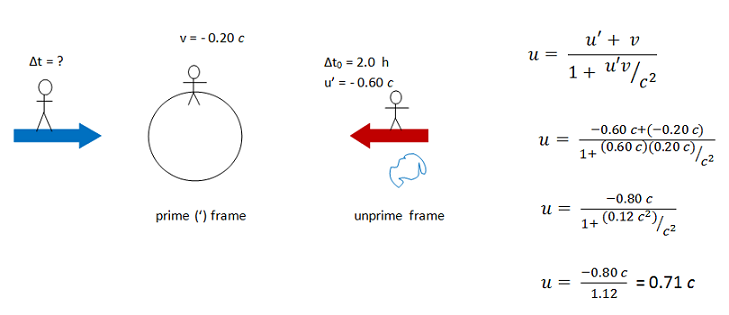
Now that you know the relative speed between the spaceships, you are ready to return to the original question. Scroll down to find the time of transit of the asteroid as measured by an observer on the second spaceship.
Why isn't the relative velocity 0.20 c + 0.60 c = 0.80 c?
Remember, the spaceships are approaching Earth and each other at relativistic speeds. Therefore, the speed at which they approach each other cannot be approximated as the sum of their speeds relative to Earth.
Why did you find the speed of the first spaceship as measured by the second? I thought you wanted to find the relative speed of the two ships.
The velocity addition equation relates the speed of a third object as measured by two different observers. In this case, we need to know the relative speed of the two ships. You can think of that relative speed as the speed of the first ship as measured by the second, or as the speed of the second as measured by the first. I chose to do the first, so that observers on Earth and the second ship measure the speed of the first ship. If you used the second approach, your signs will just be reversed.
Remember, the spaceships are approaching Earth and each other at relativistic speeds. Therefore, the speed at which they approach each other cannot be approximated as the sum of their speeds relative to Earth.
Note that there is a factor of c in both u' and v. Therefore, the c 2in the denominator cancels out.
The velocity addition equation relates the speed of a third object as measured by two different observers. In this case, we need to know the relative speed of the two ships. You can think of that relative speed as the speed of the first ship as measured by the second, or as the speed of the second as measured by the first. I chose to do the first, so that observers on Earth and the second ship measure the speed of the first ship. If you used the second approach, your signs will just be reversed.
Once you have assigned the prime and unprime frames, you can assign symbols to the quantities that are given. Because 0.60 c is the speed of the object whose speed you are measuring, it is given the symbol u. Because it is the speed of that thing according to the observer in the prime frame, it is also given a '. Therefore, 0.60 c is identified as u'. Also note that it is in the negative direction as I have drawn my picture.
Once you have assigned the prime and unprime frames, you can assign symbols to the quantities that are given. Because 0.20 c is the relative speed of the two observers (one on Earth and one on the second spaceship), it is given the symbol v. Because v does not have a ', you must assign it as the speed of the ' observer (Earth) according to the observer in the unprime frame (the second spaceship). The Earth and the second spaceship are moving toward each other, which means that the Earth is moving in the negative direction (to the left) according to the observer on the ship.
Math is easiest if the prime (') frame is that of the observer whose measurement you know. You are given the speed of the spaceship according to the observer on Earth, so it is easiest if Earth is the ' frame.
Math is easiest if the prime (') frame is that of the observer whose measurement you know, and the unprime frame that of the observer whose measurement you want to find. You want to find the speed of the first spaceship relative to (as measured by) the second spaceship, so it is easiest if the spaceship is the unprime frame.
----------------------------------------------------------------------------------------------
Step 3
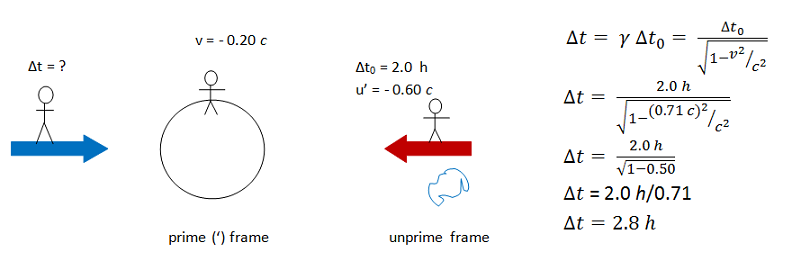
According to an observer on the second spaceship, it takes 2.8 hours for the asteroid to pass out of sight of the first ship.
Why did you use 0.71 c for v instead of 0.20 c?
In this case, the two observers whose measurements are being compared are the observers on the two spaceships. Therefore, v is the relative speed between the two ships.
As discussed in the first stage of the solution, the first spaceship is the proper frame for measuring the time of transit of the asteroid.
Note that both 0.71 and c are squared. The c2s cancel and (0.71)2 = 0.50.
Two significant figures were given in this problem and so two significant figures are included in the solution.
In this case, the two observers whose measurements are being compared are the observers on the two spaceships. Therefore, v is the relative speed between the two ships.
-
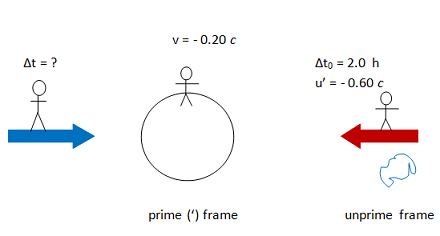
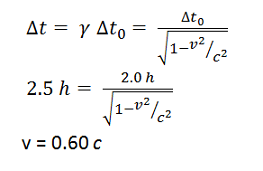
This was a three part problem. You were asked to compare time measurements made by two observers, and so it is a relativisitic time dilation problem. However, you were not given the relative speed between the observers and so had to begin by calculating that speed. The first step was to find the speeds of each of the two spaceships relative to Earth.
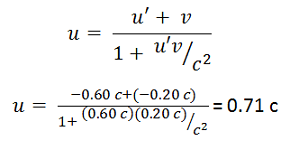
Once the speeds of the two ships relative to Earth are known, the velocity addition equation was used to find the relative speed between the ships. At this point, we were able to compare the time measurements between the ships as asked.

As expected, the observer on the second ship measures a longer time interval than the observer on the first ship. As astronaut 2 watches 2.0 hours tick off on a clock in the first ship, he sees that clock run slow so more time ticks off on his clock. The reverse is true as astronaut 1 watches a clock on ship 2. Crazy!
How do I begin? There aren't many numbers given.
It doesn't matter what was given or requested-you always work problems according to the key physics involved. As long as you begin with the physics, you can find quantities as you need them. In this case, multiple observers time the transit of an asteroid, so this is a relativistic time dilation problem.
