Different musical instruments sound different. In other words, you can distinguish a piano from a trumpet, even if they both play the same note. This is because of the relative strengths of the overtones that are present in the sound waves produced by each. What are the frequencies of the first three overtones for a piano playing a Middle C (262 Hz)? If a piano tuner found that the Middle C string actually had a fundamental frequency of 255 Hz, by what factor would he have to adjust the tension in order to tune the string? Should he increase or decrease the tension?
-
In this problem, you are directly told to consider overtones of vibration. Overtones are standing wave patterns that result from the superposition of identical waves in the same place at the same time. Therefore, this is a 1-dimensional standing wave problem. You can bring in additional definitions as you need them, but always begin with the key physics of the situation.
Overtones are the higher order normal modes of vibration of an object; each normal mode corresponds to a natural frequency of vibration. The first (simplest) normal mode is called the fundamental and in instruments its corresponding frequency determines the pitch of the note. The more complicated normal modes determine the quality of the sound and are called overtones. Overtones are numbered beginning with 1, and so the full set of normal modes is the fundamental, the first overtone, the second overtone, etc. This terminology holds regardless of the relationship between frequencies.
The fundamental frequency is the frequency of the simplest normal mode of vibration of an object. This is always the lowest frequency of the vibration. Our brains interpret the lowest frequency of vibration in a musical instrument as the pitch of the note being played.
Identical waves are waves of the same kind (waves in a string, sound waves, etc.) with the same wavelength and amplitude. In this case, as the waves travel along the piano string they are reflected back by the anchoring points at the end of the string. As a result, identical waves are traveling back and forth along the string.
The string is a one-dimensional object. A two-dimensional standing wave would be waves in and out of a 2-d surface, such as standing waves on water.
The actual vibration of an object is the sum of all of the normal modes of vibration that are present. To superpose waves, you add the amplitude of all oscillations present at each location.
Isn't this just a plug and chug problem?
If you see this as a plug and chug problem using the wave equation and the definition of the velocity of a wave in a string, that is great. Both of those equations are straightforward in both concept and mathematics. However, it is not a good idea to plug into the partially-solved versions of the wave equation that give frequency of overtones. (You can see these in the solve step of the problem.) First, by using those equations you are practicing your algebra but not understanding the physics of the situation. Second, there are different partially-solved equations for every type of instrument but the wave equation always applies. If you understand the physics, you only need to remember one equation.
-
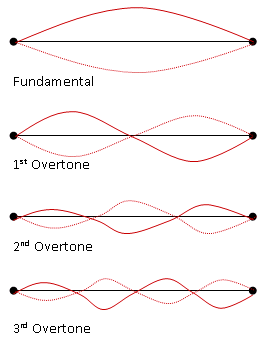
Even though you are asked for the overtones, always begin with a picture of the fundamental oscillation. The fundamental oscillation is the simplest wave pattern that meets the boundary conditions. In this case, you know that the piano strings are anchored at each end and so there are nodes at each end of the string. The simplest pattern that accomplishes this is half a wavelength.
Once you have the fundamental oscillation, you can build the overtones in order just by making them increasingly complicated. Each addition of a node takes you to a higher order overtone.
Why did you talk about adding nodes to draw the overtones? My instructor taught me to add loops.
This is the same thing. Every time you add a node into the drawing, you introduce an additional half wavelength.
You talk about wavelengths and half wavelengths, but I don't see it. I see loops in the drawings instead.
Remember that the string is continually vibrating. We draw the two extremes of the motion, so that the solid lines on the drawing represent the shape of the string as it stops moving in one direction and the dotted line represents its shape as it stops in the other direction. If you could watch the string you would see it as a blur going back and forth between those pictures. So if you don't see the wave nature in the "loop" picture, just look at the solid line (the shape of the string at one point in time.)
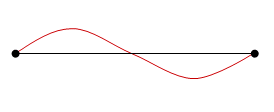
It should be straightforward to see that the solid line in the 1st overtone is one complete wavelength. When the dotted line is added in, you can then see that one wavelength corresponds to two loops. Each loop is half a wavelength.
Boundary conditions are just the conditions at the end (or edges) of the object. If we know what must be true at the edges, we know the only allowed wave patterns are those that meet those conditions.
The piano strings do not flop around at either end. Both ends are tied down and don't move. Any point in an object that doesn't vibrate is called a node and so we know the boundary condition at each end is a node.
If you go from one node to the next, you have half a wavelength. A full wavelength (as shown below) has an additional node in the middle.

The easiest way to make sure you have not skipped any overtones is to count the nodes. Keep the boundary conditions fixed and look at increasingly complicated patterns of vibration that meet those boundary conditions. The only way to keep the boundary conditions fixed is to add half-wavelengths (because they return you to the same end condition), or, in other words, to add nodes.
-
Standing wave pictures give a picture of, and a way to measure, the the wavelength of the oscillation of interest. In this case, you are asked to consider the frequencies associated with the wavelengths. Wavelength and frequency are always related by the wave equation:
v = f λ
If at this point you also recognize that in later questions you will need the definition of the velocity of a wave in a string that is great. If you do not see that part of the problem yet, that is fine. You will come to the additional question as you work the problem. Velocity of a wave in a string is given by
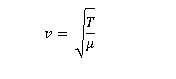
Why do you want velocity of a wave in a string? A piano produces sound waves. Shouldn't you use the velocity of sound?
The wave the moves from the instrument to your ear is a sound wave and propogates with the speed of sound. However, in this problem you are relating wavelength of the wave in the string to the frequency of vibration.
The wave equation is just a re-write of the defintion of velocity (change in displacement over time) for the specific case of waves. By definition, it takes one period for the wave to travel one wavelength.
Be careful of symbols. T in this equation is tension in the string and not period of oscillation. Some books overcome this confusion by using F for force. In either case, the velocity of a wave in a string depends on the tension in the string.
-


We now know the frequencies of the first three overtones. Scroll down to consider how to tune the piano string.
I don't have any numbers. Don't I need to know the wavelength of the wave in order to solve for the frequency?
In this case, you do know the fundamental frequency of the string. Any time you are comparing cases, it is likely that you can solve the problem with ratios (and the unknowns will cancel out) or by solving the known case for a group of variables together as I do here. If you are not sure if this approach will work, as a general rule of thumb you don't need to know all variables if your relation involves only multiplication and division and if you know information about one case.
Can I use the information about fundamental frequency to solve for the length of the string?
Although that is not the most efficient approach (see previous Query Question above), you can often use a known case to solve for unknown variables that appear in the second case. However, that approach will not work for this problem because you also don't know the velocity of the wave in the string.
Why can't I just use the relation fovertone = n ffundamental?
It is not a good idea to plug into this partially-solved version of the wave equation. First, by using this equation you are practicing your algebra but not understanding the physics of the situation. Second, there are different partially-solved equations for every type of instrument but the wave equation always applies. If you understand the physics, you only need to remember one equation.
Remember, you are applying the wave equation to the standing wave in the string and not to the sound wave that goes from the piano to your ear. So v in this equation refers to the speed of the wave in the string and not the speed of sound.
In this case, half a wavelength fits between the nodes at the ends of the string. The length of the string is equal to half a wavelength, so the wavelength is twice the length of the string.
In this case, one entire wavelength fills the string. λ = L.
In this case, one wavelength fills 2/3 of the string. λ = 2/3 L.
For this overtone, two complete wavelengths fit on the string, or one wavelength is half the length of the string.
ffund = v/(2L)
f1 = v/L = 2v/(2L) = 2 ffund
To divide by a fraction, invert and multiply. 1/(2/3) = 1 x (3/2)
ffund = v/(2L)
f3 = v/(1/2 L) = 2v/L =4 v/(2L) = 4 ffund
----------------------------------------------------------------------------------------------
Step 2
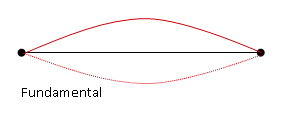
The problem tells us that the piano tuner adusts the pitch of the note by changing the fundamental frequency, and so we only need to look at the first picture.
Furthermore, we are told that he adjusts the frequency by adjusting the tension. If you did not previously realize that you need to use the definition of velocity of a wave in a string, you would see it now.
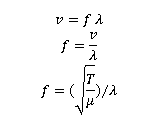
At this point, you can answer the conceptual part of the question. The frequency of the string's vibration is too low, and so in order to increase the frequency you need to also increase the tension. To quantize the amount by which tension needs to be adjusted, compare the two cases as a ratio.
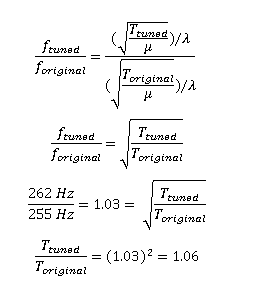
The tension in the string needs to be increased by a factor of 1.06, or 6 %, in order to tune the string.
Remember, the wave in question is the wave in the piano string and not the sound wave that goes from the piano to your ear. So you do not use the speed of sound in this equation. Instead you must use the speed of the wave in a string.
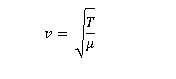
From the previous step, you know that the wave equation gives you a relationship to quantize the frequency of the vibration. Wavelength is fixed because the string does not change in length as you tune it. Therefore, the only way you can affect frequency is through the wave's velocity.
Tension is in the numerator of the relationship for v, so as tension increases velocity also increases.
You do not need to know length and linear density of the string. Whenever you compare two cases it is likely that you can cancel unknowns if you relate the two situations through a ratio. As long as there are only two terms (A = B) this approach will work.
μ (linear density of the string) and λ (wavelength = 2 x the length of the string) do not change as the string is tuned. Therefore, they each cancel out in the equation.
-
In this problem, the word "overtones" should flag that you want to examine standing waves in a string, even if you aren't yet comfortable recognizing the relationship between standing waves, resonance, and musical instruments. All you need in order to understand 1-dimensional standing waves is a picture of the waves and the wave equation.
That said, if you play a musical instrument make sure to relate your answers to your musical knowledge. You may know that the frequency of a note doubles each octave, for example, and so you may recognize the first overtone as being the C one octave above Middle C. You also know that as you tighten a guitar string the pitch of the string gets higher, in agreement with your conceptual answer to the second part of the problem. You can now explain that effect because you recognize that tightening the string increases the speed of the wave in the string. If wavelength is fixed by the instrument, f must increase so that v = f λ remains true.
The frequencies that you hear in a musical instrument are those that resonate--that correspond to strong waves in the string or air column and do not cancel out. Resonant frequencies are associated with normal modes of oscillation.
My book talks about harmonics not overtones. Are overtones the same as harmonics?
Overtones and harmonics represent the same basic idea but are numbered differently. In both cases, you are looking at the normal modes of vibration of the instrument; each normal mode corresponds to a natural frequency of vibration. The first (simplest) normal mode is called the fundamental and its corresponding frequency determines the pitch of the note. The more complicated normal modes determine the quality of the sound and are called overtones. Overtones are numbered beginning with 1, and so the full set of normal modes is the fundamental, the first overtone, the second overtone, etc. This terminology holds regardless of the relationship between frequencies.
Naming normal modes as harmonics, on the other hand, is based on frequency. If the frequency of a normal mode is an integer multiple of the fundamental frequency, then that normal mode is also called a harmonic. Harmonics are determined by the integer multiplier. Since the frequency of the first normal mode is 1 x the fundamental frequency, the first normal mode is also the first harmonic. Not all harmonics are present in all objects. For example, in a closed pipe, the frequencies corresponding to the normal modes are 1, 3, 5, etc. times the fundamental frequency, and so only odd overtones are present.
