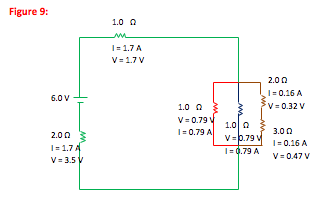
What is the current through, and voltage drop across, each resistor in the following circuit?
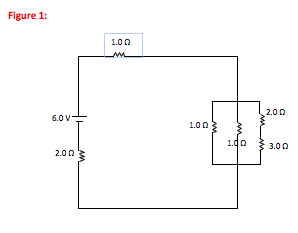
-
In this problem, you are asked to find current and voltage drop in an electric circuit. Any time that you are given an electric circuit and asked for properties associated with that circuit (current, resistance, voltage, charge, capacitance) you will work the problem in one of two ways.
If the circuit is straightforward and you can track the flow of current, the best approach is to use a basic understanding of circuits to work the problem. If, however, the circuit contains a Wheatstone Bridge or is, in general, too complicated to track the current, then you will need to use Kirchhoff’s Laws (note: this link will take you to different problem).
In this example, I will use a basic understanding of circuits to work the problem.
-
The first thing you need to do in a circuit problem is reduce the circuit to a single equivalent resistance (or capacitance.)
Hint: The most frequent mistakes made in these problems come about from skipping this step or doing too many things at once. If you carefully reduce the circuit and record your drawings along the way (I like to put each drawing in a column along the left side of my paper so that I can work my way back up), you may be able to take shortcuts in later steps. But don’t take shortcuts now!
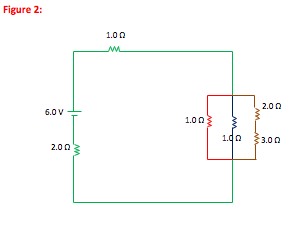
It is handy for these problems to use colors to track sections of the circuit where current is the same. So before I begin to reduce the circuit, I use colored pencils or highlighters to trace the currents. A single color means that current is the same throughout that path.
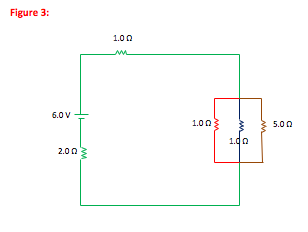
For resistors in series,
Req = ∑i
Ri = 2.0 Ω + 3.0 Ω = 5.0 Ω
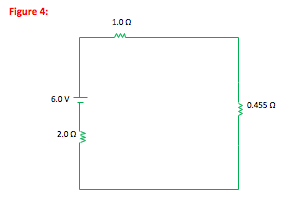
For resistors in parallel,
1/Req = ∑i
(1/Ri) = 1/(1.0 Ω) + 1/(1.0 Ω) + 1/(5.0 Ω) = 2.2 Ω-1
Req = 1/(2.2 Ω-1) = 0.455 Ω.
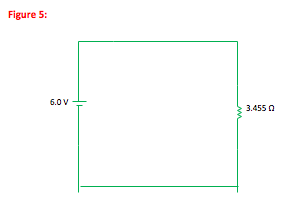
-
There are two ideas (charge is conserved, energy is conserved) and three equations that help you understand circuits.
As applied to circuits,
Conservation of Charge gives: Current is the same through resistors in series.
Conservation of Energy gives: Voltage drop is the same across each leg of a parallel circuit.
The three equations are
1.) Req = ∑i Ri
2.) 1/Req = ∑i (1/Ri)
3.) ΔV = IR
You already used Conservation of Charge and the first two equations as you drew the pictures. To solve the problem, you will use Conservation of Energy, Conservation of Charge, and the third equation.
-
Note: In this example, I use color in branches of the circuit, calculations, and descriptions. Note that all elements in a given color relate to each other.
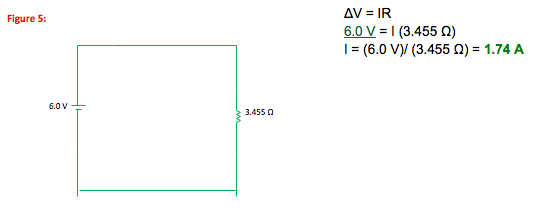
1.74 A of current come through the battery. The current everywhere that is color-coded green and bolded is also 1.74 A (there are no junctions in the green portion of the circuit.)

We now know the current and voltage drop across the 1.0 and 2.0 Ω resistors in the series portion of the circuit, so those resistors require no further calculation.
Check: 1.7 V + 3.5 V + 0.79 V = 6.0 V. The voltage gain across the battery is balanced by conversions across the resistors.
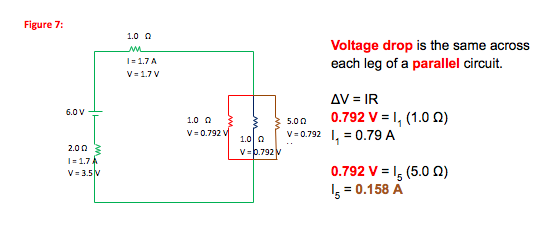
Check: 0.79 A + 0.79 A + 0.16 A = 1.74 A. Current is conserved in and out of the junction.
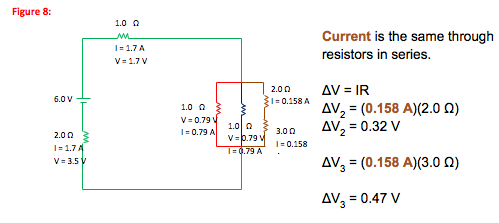
Check: 0.32 V + 0.47 V = 0.79 V = drop across parallel branch
How do I approach a circuit with capacitors instead of resistors?
In exactly the same way! The relation ΔV = IR that you use for resistors is replaced with ΔV = Q/C, and capacitors in parallel add according to Ceq = ∑iCi, while capacitors in series add according to 1/Ceq = ∑i(1/Ci). The approach that you use, however, is identical.
How can I work this circuit using Kirchhoff’s Laws?
Why is use of Kirchhoff’s Laws not the best approach for working this problem?
Although Kirchhoff’s Laws will work in any circuit, they have two disadvantages.
First, they require a lot of linked algebraic equations. (In this problem you would need to jointly solve four equations in four unknowns, and this one is pretty direct.)
Second, you do not need to know or learn anything at all about the physics of circuits to use Kirchhoff’s Laws. So working circuits that way will strengthen your algebraic skills, but will not help you with conceptual questions about circuits. If you use the basic ideas behind circuits on practice problems, you will find that you can answer many mathematical and conceptual questions without having to fully go through all mathematical steps.Why did you start with the 2.0 and 3.0 Ω resistors?
You will save steps if you begin to reduce the circuit by starting within parallel branches and working out. In this case, the 2.0 and 3.0 Ω resistors are in series with each other within a larger parallel section of the circuit. I cannot reduce that parallel section until I first reduce this series component within it. From the perspective of the battery and the current through each wire, it is equivalent to replace the 2.0 and 3.0 Ω resistors with a single 5.0 Ω resistor.
Isn’t the equivalent resistance of the parallel portion of the circuit 2.2 Ω.?
OrIsn’t the equivalent resistance of the parallel portion of the circuit 7.0 Ω.?
It is very common to make math errors when solving for the equivalent resistance of a parallel circuit.
Remember that (1/a) + (1/b) is NOT equal to 1/(a + b)!
Also, remember to take the inverse of your sum at the end—the sum is equal to 1/Req and not to Req.Are there faster ways to solve this?
As long as you work within each picture at one time (so that you don’t inadvertently combine series and parallel portions together), it is fine to reason out currents and voltages without using the equation. For example, if you recognize that the current across the 5.0 Ω resistor is 1/5 as much as that across the 1.0 Ω resistor, you can think of the current as being made of 11 parts. 5 parts go across each 1.0 Ω resistor and one part goes across the 5.0 Ω resistor.
(5/11)(1.74 A) = 0.79 A
(1/11)(1.74 A) = 0.158 AAlthough Kirchhoff’s Laws will work in any circuit, they have two disadvantages.
First, they require a lot of linked algebraic equations. (In this problem you would need to jointly solve four equations in four unknowns, and this one is pretty direct.)
Second, you do not need to know or learn anything at all about the physics of circuits to use Kirchhoff’s Laws. So working circuits that way will strengthen your algebraic skills, but will not help you with conceptual questions about circuits. If you use the basic ideas behind circuits on practice problems, you will find that you can answer many mathematical and conceptual questions without having to fully go through all mathematical steps.The battery has no knowledge of the details of the circuit. Any circuit that has the same equivalent resistance will yield the same current through a given battery. In other words, if you take out this circuit and replace it with a single resistance of the “equivalent” amount, the battery will not know the difference and you will have the same amount of current. That single equivalent resistance is the starting place for solving a circuit problem.
Charge is conserved—in other words, current is the same in any series portion of the circuit (where there are not alternate paths.) It is true that electric potential energy is converted into other forms when current goes through a resistor, but the electrons themselves do not get used up. Current stays the same. At a junction, some of the current will follow each path but it still must add to the total value.
You will save steps if you begin to reduce the circuit by starting within parallel branches and working out. In this case, the 2.0 and 3.0 Ω resistors are in series with each other within a larger parallel section of the circuit. I cannot reduce that parallel section until I first reduce this series component within it. From the perspective of the battery and the current through each wire, it is equivalent to replace the 2.0 and 3.0 Ω resistors with a single 5.0 Ω resistor.
Once each branch within a parallel portion of a circuit has been reduced to a single resistance, the parallel portion of the circuit itself can be reduced. In this case, if the parallel portion of the circuit were replaced with a single 0.455 Ω resistor, the amount of current through the battery would not change.
Note that resistance of a parallel branch should be less than the resistance of any individual branch. By providing more space for the current to flow, there is less resistance. (Think of water in pipes—multiple pipes allow more water to flow than even the largest of the individual pipes.It is very common to make math errors when solving for the equivalent resistance of a parallel circuit.
Remember that (1/a) + (1/b) is NOT equal to 1/(a + b)!
Also, remember to take the inverse of your sum at the end—the sum is equal to 1/Req and not to Req.Once the parallel portion of the circuit has been reduced to a single resistor, you can see that the net resistance of the circuit is equal to that of a 1.0, a 2.0 and a 0.455 Ω resistor in series with each other. There will be the same amount of current through the battery if these three resistors are replaced by a single 3.455 Ω resistor.
Some books use V instead of ΔV in this equation. I use ΔV to emphasize that this equation quantifies the change in voltage across a resistor.
When the circuit reaches its steady state, the amount of energy (per charge) that the current gains as it goes across the battery is equal to the amount of energy (per charge) that it converts to other forms in the resistors. This balance is what determines how much current comes out through the battery. This understanding can be restated as “voltage drop is the same across each leg of a parallel circuit.” Regardless of which path the current takes, it must convert the same amount of energy (per charge) to other forms.
Once you have reduced the circuit to a single resistor, the voltage drop across that equivalent resistor is equal to the voltage gain across the battery.
Make sure to work with a single drawing at a time and not to skip intermediate circuits. Once you know the “green” current, you can find voltage drop across all real and calculated resistors which experience that current. Likewise as you move from drawing to drawing you will always carry current or voltage drop with you for a single section of the circuit.
As long as you work within each picture at one time (so that you don’t inadvertently combine series and parallel portions together), it is fine to reason out currents and voltages without using the equation. For example, if you recognize that the current across the 5.0 Ω resistor is 1/5 as much as that across the 1.0 Ω resistor, you can think of the current as being made of 11 parts. 5 parts go across each 1.0 Ω resistor and one part goes across the 5.0 Ω resistor.
(5/11)(1.74 A) = 0.79 A
(1/11)(1.74 A) = 0.158 AHow do I work a problem in which I have capacitors in a circuit?
In exactly the same way! The relation ΔV = IR that you use for resistors is replaced with ΔV = Q/C, and capacitors in parallel add according to Ceq = ∑iCi, while capacitors in series add according to 1/Ceq = ∑i(1/Ci). The approach that you use, however, is identical.
Help! I have a very complicated circuit and have no idea how to reduce it to a single equivalent resistance. What do I do?
This is the only case in which I recommend using Kirchhoff’s Laws. Click here to solve this circuit with Kirchhoff’s Laws.
How do I work a problem in which I have capacitors in a circuit?
In exactly the same way! The relation ΔV = IR that you use for resistors is replaced with ΔV = Q/C, and capacitors in parallel add according to Ceq = ∑iCi, while capacitors in series add according to 1/Ceq = ∑i(1/Ci). The approach that you use, however, is identical.
Help! I have a very complicated circuit and have no idea how to reduce it to a single equivalent resistance. What do I do?
This is the only case in which I recommend using Kirchhoff’s Laws. Click here to solve this circuit with Kirchhoff’s Laws.
-

In this problem, you first use the understanding that current is the same through all series portions of a circuit and the equations for equivalent resistance to replace the given circuit with one that has the same effect from the perspective of the battery.
This break down of the circuit into one equivalent resistance is the key to working circuit problems successfully. Start within parallel components of the circuit and work out, and don’t take more than one step at a time.
Once you know the equivalent effect of the circuit on the battery, you can use the understanding that voltage drop is the same across parallel legs of a circuit (conservation of energy) and the equation defining the voltage drop across a resistor to find the current and voltage drop for each resistor.
Keeping track of your information is key. At each step, if you fill what you know into the appropriate intermediate drawing you are far less likely to make mistakes. If you replaced a series of resistors with a single resistor, the current through all is the same. Likewise, if you replaced a parallel portion of the circuit with a single resistor, the voltage drop across all is the same.
In this case, there is a current of 1.7 A through the battery. At the junction to the parallel legs of the circuit, the current splits. Just over 45% of the current goes through each of the 1 Ω resistors, and 9.1% of the current goes through the 5 Ω resistor. No current is used up, but electric potential energy is converted to other forms in each resistor.
