What is the current through, and voltage drop across, each resistor in the following circuit?
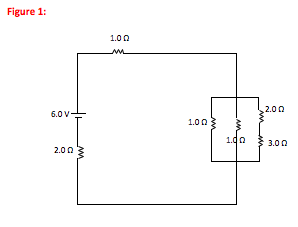
-
In this problem, you are asked to find current and voltage drop in an electric circuit. Any time that you are given an electric circuit and asked for properties associated with that circuit (current, resistance, voltage, charge, capacitance) you will work the problem in one of two ways.
If the circuit is straightforward and you can track the flow of current, the best approach is to use a basic understanding of circuits to work the problem. If, however, the circuit contains a Wheatstone Bridge or is, in general, too complicated to track the current, then you will need to use Kirchhoff's Laws.
In this example, I will model the use of Kirchhoff’s Laws to work the problem.
-
Hint: When working a circuit problem with Kirchhoff's Laws, you need to keep track of all the different currents. If you recognize that current is the same through all resistors in series, you reduce the number of unknowns in your problem. I find that color-coding the circuit to show each region of “same” current helps to avoid record-keeping mistakes.
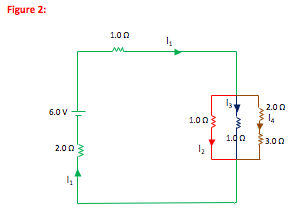
-
In this example, I chose to model solving a circuit with Kirchhoff's Laws.
1. Current into a junction = current out of that junction
2. The change in voltage around any loop of the circuit = 0
Once you know current through a resistor, voltage drop is given by
ΔV = IR -
Step 1:


Now that you have found the current through each resistor, scroll down to find the voltage drop across each resistor
--------------------------------------------------------------------------------------------
Step 2:
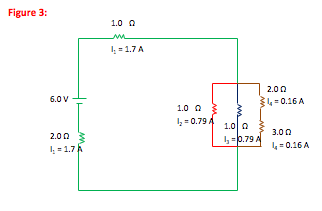

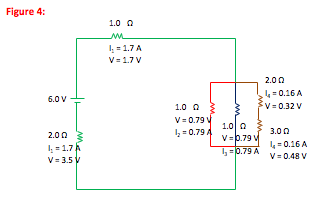
How do I approach a circuit with capacitors instead of resistors?
Kirchhoff’s Laws are not a good model for the approach to working circuits of capacitors. Click here to solve this circuit using an approach that applies equally well to capacitors. In that case, the relation ΔV = IR that you use for resistors is replaced with ΔV = Q/C, and capacitors in parallel add according to Ceq = ∑iCi, while capacitors in series add according to 1/Ceq = ∑i (1/Ci). The approach that you use, however, is identical.
How can I work this circuit without using Kirchhoff’s Laws?
How did you know which way the current flows?
OrWhy do you need to specify the direction that current flows?
Kirchhoff's Laws require you to know (or guess) at the direction of each current. (If you guess wrong, you will get a negative sign in your answer.) When you use the loop rule, you will put in –IR when you go across a resistor with the direction of current and a +IR when you cross the resistor against current. You need to be consistent and so should mark the direction of current on your drawing.
In this case, the circuit is straightforward. Current flows "out" of the + side of a battery, around the circuit, and "into" the – side, or, in this case, clockwise around the circuit.How do we know current is the same through all resistors in series?
Charge is conserved—in other words, current is the same in any series portion of the circuit (where there are not alternate paths.) It is true that electric potential energy is converted into other forms when current goes through a resistor, but the electrons themselves do not get used up. Current stays the same. At a junction, some of the current will follow each path but it still must add to the total value.
How did you know which order to solve the equations?
When you have multiple equations in multiple unknowns, it doesn’t matter what order you use to solve them. It will always work if you pick one equation, solve it for any one variable, put that expression back into the remaining equations, and repeat to eliminate a different variable until you finally have a single equation with one unknown. That is the approach I used here, first eliminating I3, then I1, then I4 so that I could solve for I2.
Why do you only have one junction equation?
You can write junction equations for all but one of the junctions-that last equation will always be redundant. In this case, you can see that the equation for either junction is identical to the other.
How do you know which loops to pick?
You need a total of four equations (because you have four unknown currents.) Because you have one junction equation, you need three loop equations. Any three loops will do.
In this case, I took the loop through the battery, around through the left-most resistor in the parallel portion of the circuit, and back to the battery.Whenever current comes to a junction, it splits. Some of the original current follows each of the possible paths. Current remains the same over any portion of the circuit where there is no junction.
Charge is conserved—in other words, current is the same in any series portion of the circuit (where there are not alternate paths.) It is true that electric potential energy is converted into other forms when current goes through a resistor, but the electrons themselves do not get used up. Current stays the same. At a junction, some of the current will follow each path but it still must add to the total value.
Kirchhoff's Laws require you to know (or guess) at the direction of each current. (If you guess wrong, you will get a negative sign in your answer.) When you use the loop rule, you will put in –IR when you go across a resistor with the direction of current and a +IR when you cross the resistor against current. You need to be consistent and so should mark the direction of current on your drawing.
In this case, the circuit is straightforward. Current flows "out" of the + side of a battery, around the circuit, and "into" the – side, or, in this case, clockwise around the circuit.A junction is any point in the circuit where current can split or where several currents come together.
Charge is conserved. It is true that electric potential energy is converted into other forms when current goes through a resistor, but the electrons themselves do not get used up. Current stays the same. At a junction, some of the current will follow each path but it still must add to the total value.
Batteries convert chemical energy to electric potential energy and resistors convert electric potential energy to other forms. Therefore, if you follow in the direction of current, batteries boost the voltage of the charges (by the voltage of the battery) and resistors reduce the voltage of the charges (by ΔV = -IR.) If you trace a loop against current, the signs are reversed.
A loop is just any closed path in the circuit—a path that starts and ends at the same point.
Once a circuit reaches its steady state current, the boosts to energy provided by the battery are exactly balanced by the decrease in electric potential energy due to the resistors. Therefore, over any closed path (start and end at the same point), Conservation of Energy tells us that the net change in voltage is zero.
You can write junction equations for all but one of the junctions-that last equation will always be redundant. In this case, you can see that the equation for either junction is identical to the other.
A junction is any place that multiple wires join.
You need a total of four equations (because you have four unknown currents.) Because you have one junction equation, you need three loop equations. Any three loops will do.
In this case, I took the loop through the battery, around through the left-most resistor in the parallel portion of the circuit, and back to the battery.You need a total of four equations (because you have four unknown currents.) Because you have one junction equation, you need three loop equations. Any three loops will do.
In this case, I took the loop through the battery, around through the right-most resistor in the parallel portion of the circuit, and back to the battery.You need a total of four equations (because you have four unknown currents.) Because you have one junction equation, you need three loop equations. Any three loops will do.
In this case, I took the loop up through the left-most resistor in the parallel portion of the circuit, and back down through the middle resistor in the parallel section.When you have multiple equations in multiple unknowns, it doesn’t matter what order you use to solve them. It will always work if you pick one equation, solve it for any one variable, put that expression back into the remaining equations, and repeat to eliminate a different variable until you finally have a single equation with one unknown. That is the approach I used here, first eliminating I3, then I1, then I4 so that I could solve for I2.
6.0 V = I1 (1.0 Ω) + I2 (1.0 Ω) + I1 (2.0 Ω)
6 = 1 I1 + 1 I2 + 2 I1
6 = 3 I1 + I26.0 V = I1 (1.0 Ω) + I4 (2.0 Ω) + I4 (3.0 Ω) + I1 (2.0 Ω)
6 = 1 I1 + 2 I4 + 3 I4 + 2 I1
6 = 3 I1 + 5 I4This example is for resistors in a circuit. How do I work a problem in which I have capacitors in a circuit?
Kirchhoff’s Laws are not a good model for the approach to working circuits of capacitors. Click here to solve this circuit using an approach that applies equally well to capacitors. In that case, the relation ΔV = IR that you use for resistors is replaced with ΔV = Q/C, and capacitors in parallel add according to Ceq = ∑iCi, while capacitors in series add according to 1/Ceq = ∑i (1/Ci). The approach that you use, however, is identical.
-

In this problem, you use Kirchhoff's Laws to find the current through each resistor in a circuit. Kirchhoff's Laws are Conservation of Charge and Conservation of Energy applied to circuits. Although you can use them without understanding the circuit, once you have also used ΔV = IR for each resistor, you should go back through the circuit to follow the current and track the energy.
In this case, there is a current of 1.7 A through the battery. At the junction to the parallel legs of the circuit, the current splits. The total current in the parallel section (0.79 A + 0.70 A + 0.16 A) = 1.7 A, or the current through the battery, as it should. .
No current is used up in resistors, but electric potential energy is converted to other forms in each resistor. In the steady state, the energy (per charge) provided by the battery is completely converted to other forms over any path that the current can follow. In this case, the battery provides a potential difference of 6.0 V. Through any branch of the parallel portion of the circuit, the current loses 0.8 V. Therefore, over any path the current loses (1.7 V + 0.8 V + 3.5 V) = 6.0 V as expected.
