Your friend is moving into a new apartment. He has a 4.0 foot tall mirror that he wants to hang on his wall so that he can see himself fully in it. If your friend is six foot four, how high should he hang the mirror? Assume that his eyes are four inches below the top of his head.
-
Mirrors reflect light. To understand what you see or how you see it when looking in a mirror, you need to think about how light is reflected.
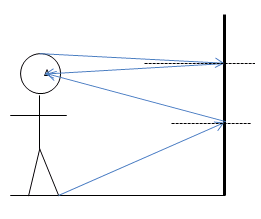
In order to understand what we see in a mirror, we need to draw the light rays that get to our eyes. In this case, your friend wants to see all of himself. As long as he can see his feet and the top of his head, the mirror is located well on the wall. Therefore, you need to draw the light ray that goes from his feet to his eyes, and the light ray that goes from the top of his head to his eyes.
I don't know where the focal point is. How do I draw the principle rays?
Drawing principle rays is helpful for understanding how light waves reflect off of mirrors with curved surfaces. However, for plane (flat) mirrors, the rule that the angle of reflection is equal to the incident angle is straightforward to apply. No need to draw principle rays. (Incidentally, the focal length for a plane mirror is infinity.)
How do you know which rays to draw?
Light is scattered (reflected in all directions) off of every point in your friend's body as shown for his foot below. However, only a very few of those light rays get to your eye. Those are the rays that you see, and so those the only rays that you need to draw.
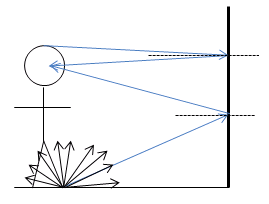
Your friend needs to position the mirror so that the bottom edge is low enough to show him his feet, and the top edge is high enough to show his head. Any location that meets those criteria will work.
Light is scattered (reflected in all directions) off of every point in your friend's body as shown for his foot below. However, only a very few of those light rays get to your eye. Those are the rays that you see, and so those the only rays that you need to draw.

We know that light reflects off of a surface with the same angle relative to the normal as it had coming in: Θi = Θr. Therefore, you can trace the path of the light rays by drawing straight lines until they get to the mirror. Use Θi = Θr to find the outgoing direction of the wave. The light that shows your friend his foot is the ray that leaves his foot, bounces off the mirror, and enters his eye.
We know that light reflects off of a surface with the same angle relative to the normal as it had coming in: Θi = Θr. Therefore, you can trace the path of the light rays by drawing straight lines until they get to the mirror. Use Θi = Θr to find the outgoing direction of the wave. The light that shows your friend the top of his heat is the ray that leaves his pate, bounces off the mirror, and enters his eye.
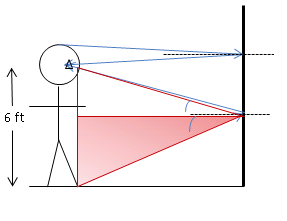
Beyond the understanding that Θi = Θr (used in the Draw a Picture stage), understanding the reflection off a plane mirror just requires geometry. At the most, you may need to call on the definitions of sine, cosine or tangent, but more likely you will compare similar triangles.
Can't I use 1/f = 1/o + 1/i?
No. This equation is useful for curved lenses and mirrors. Because the focal length of a plane mirror is infinity, all it tells you here is that your friend's image is as far behind the mirror as he is in front of it. This equation does not give any information about the vertical properties of the image.
Similar triangles are triangles of the same shape--in other words, with the same angles. The ratio of lengths of sides is the same for similar triangles, even if the triangles themselves are not the same size. Because Θi = Θr, the triangle formed by the reflected ray is similar to the triangle formed by the incident ray, and so similar triangles appear in plane mirror problems.
In this problem, all you will need is an understanding of similar triangles.
sinΘ = (opposite side)/hypotenuse; cosΘ = (adjacent side)/hypotenuse; tanΘ = (opposite side)/(adjacent side).

Note that the two triangles outlined in red (one shaded and one clear) are similar triangles. Furthermore, they share a horizontal side so they are similar triangles of the same size. This means that the two vertical sides are the same length. Since they add to 6 ft, each vertical side is 3 feet. Your friend will be able to see his feet as long as the bottom of the mirror is no more than 3 feet off the floor.
You can repeat this analysis for the top of your friend's head. In that case, the two sides of the similar triangles add to 4 inches, so each side is 2 inches. Your friend will be able to see the top of his head as long as the top of the mirror is at least 6' 2" off the floor.
So where should he put the mirror?
The bottom of the mirror must be no more than 3 feet off the ground, and the top at least 6 feet 2 inches off the ground, so as long as the mirror is at least 3 feet 2 inches tall your friend will be able to see himself. His mirror is 4 feet tall so he has a range of 10 inches (the bottom of the mirror can be anywhere from 2 feet 2 inches to 3 feet off the ground) in location that will still work.
Both are right triangles, and the angle of incident and the angle of reflection are the same. So all three angles in each triangle must be the same.
Remember, your friend's eyes are 4" below the top of his head. 6' 4" - 4" = 6'.
The horizontal distance from your friend to the mirror is the same for each triangle. Therefore, not only are the triangles similar but they are the same (just inverted.) Like sides, then, are of the same length. If they add to 6', each must be 3'.
Take a look at the drawing. If you slide the mirror down, there will still be a reflecting surface where you need it in order to direct a ray from your friend's foot to his eye.
Your friend is 6'4" tall. The top of the mirror must be at most 2" below the top of his head, or 6'2" above the ground.
The horizontal distance from your friend to the mirror is the same for each triangle. Therefore, not only are the triangles similar but they are the same (just inverted.) Like sides, then, are of the same length. If they add to 4", each must be 2".
Take a look at the drawing. If you slide the mirror up, there will still be a reflecting surface where you need it in order to direct a ray from your friend's pate to his eye.
Mirrors redirect light waves by reflecting them off the surface of the mirror. Your brain interprets the light that gets to your eye as if it traveled in a straight line and so your friend sees an image of himself that looks like it is coming from behind the mirror.
As long as the mirror is high enough to reflect a ray of light from your friend's head to his eye, he will see his head. As long as it is low enough to reflect a ray of light from his foot to his eye, he will see his foot. You know that light will travel in a straight line unless it comes to an interface, and so you are able to draw the paths that the light rays take between your friend and his eyes. It is only a matter of using geometry to relate the distances in your figure.
Now is also a good time to return to the first FAQ. Note that regardless of the distance between your friend and the mirror, the vertical sides of the lower triangles are equal and add to six feet, and the vertical sides of the upper triangles are equal and add to four inches. As long as the mirror is at least half your friend's height and hung correctly, he will be able to see himself no matter how far back he stands. If you feel that your experience is contrary to this result, pay very careful attention next time you look in a mirror. There is a distance effect for a mirror hung at a slant, but not for a vertical mirror.
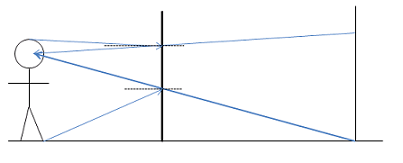
Don't I need to know how far from the mirror my friend intends to stand?
It turns out that distance from the mirror doesn't matter. You will be able to see that from the similar triangles made by the rays of light. But, as always, start the problem with a focus on the key physics. If you are confident in your choice of physics approach, you can worry about what is and isn't given when it is time to fill in numbers.
I don't have any equations for flat mirrors. How do I begin?
The key physics behind mirrors is reflection, and you know that the angle of incidence is equal to the angle of reflection. It is very important in plane (flat) mirror problems to begin with a picture to help you visualize and remember your geometry.
