Magnifying Glass - Physics - University of Wisconsin-Green Bay

Lenses work by refracting, or bending, light. For spherical lenses, the effects of refraction are summarized in how we draw and understand the principle rays. In other words, any time you are asked to understand image formation by a spherical lens, it is likely to be a geometric optics problem.

Whenever you look at something in a mirror or through a lens, you see an image of the object--your brain interprets the light waves that strike your eye as if they traveled in a straight line. In this case, you are told that the image is larger than the object (letters in the book). The word "magnify" should flag to you that this is a geometric optics problem even if the general description of the physics did not.

A spherical lens is any lens whose surface is part of a sphere. The term does not mean that the lens is an entire sphere.

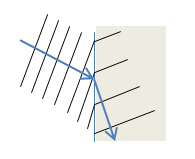
When light enters a new medium, it changes speed. If part of the light wave enters the new material first, it will slow down or speed up before the rest of the wave. As you can see in the picture below, the net effect is that the wave changes direction. If the drawing doesn't make sense to you, think of the wavefronts (black lines) as rows of marchers in a band. As each band member crosses the line, he or she picks up speed.

Go the Draw a Picture page for a detailed discussion of what the principle rays represent and how to draw them.
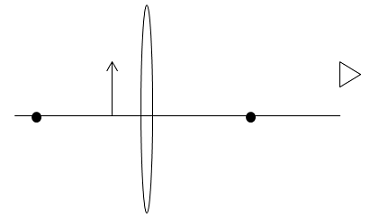
In this side view drawing, the arrow represents the object you are looking at--the book--and the triangle represents your eye. Note that in order for you to see the image rather than the object, light must leave the book, travel through the lens, and travel to your eye. Therefore, the lens is located between the object and your eye.

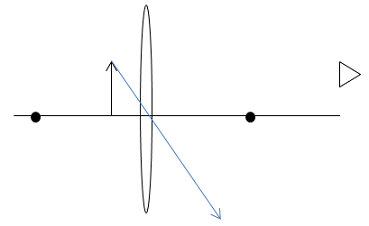
To locate the image, we need to draw the three principle rays from the top of the object and trace them to your eye. The easiest principle ray to draw is the one that leaves the top of the object, enters the center of the lens and continues on in a straight line:

The second principle ray leaves the top of the object traveling parallel to the optic axis. When it reaches the lens, it changes direction and goes out through the focal point:

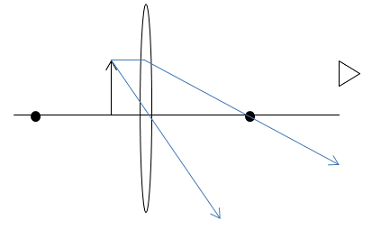
Finally, the third principle ray goes into the lens on a line that passes through the top of the object and the focal point. It changes direction in the lens and goes out parallel to the optic axis.

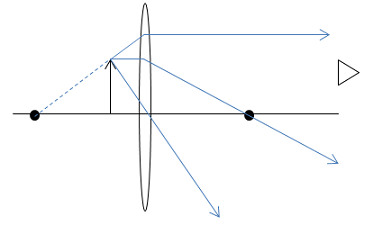
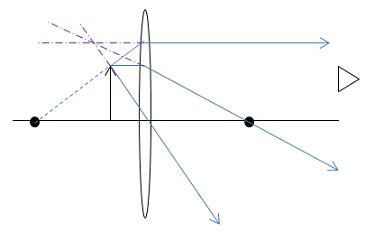
To understand where the image is located, you need to trace the rays that reach your eye back to the point where they appear to intersect.

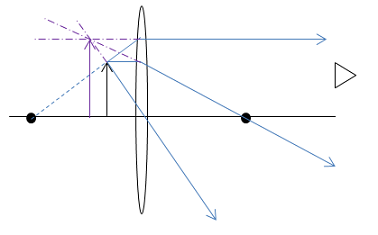
You now have a picture that illustrates not only the location of the image but also shows a visual understanding of how that image is located and sized.
- View Queries
How do you know the object is inside the focal length?

If you did not know this fact about magnifying glasses from memory, you would quickly catch your error when you drew principle rays for an object outside the focal point, as you would end up with an inverted image. That said, it is an observation worth making. Take any convex lens and hold it a far distance from an object. You should see an inverted image when you look through the lens. As you bring the lens closer and closer to the object, watch how the image changes. When it gets fuzzy and then flips, you have crossed to the point where the object is now within the focal distance of the lens.

Do I really have to make this drawing? Can't I just go straight to the equations?

It is true that in terms of equations this is just a two step "plug and chug" problem. But it is well worth your time to draw the principle rays for two reasons. The first is pragmatic--your instructor will likely require you to draw princple rays on your exam. The second relates to learning. By drawing the principle rays you have a strong visual to help you understand the physics of how the image is formed. That visual and understanding will also help you catch common errors in your math--for example, using an incorrect sign for image distance or focal length.

Hold on! I thought convex lenses caused rays to converge. The outgoing rays in the drawing are still diverging.

That is true. However, the outgoing rays are diverging less than the incident rays. You can see this by looking at the angular spread in the rays coming from each arrow. The incident rays (shown in blue leaving the top of the black arrow) spread over a much greater angle than the outgoing rays (trace the purple rays back to their intersection.)

So in this case, the lens did act to converge the rays relative to their initial path. It was not strong enough, however, to change their direction enough to make them intersect. Note that this gives you another understanding of focal length. As long as an object is outside the focal distance, the angular spread of rays that reach the lens is small enough for the lens to bring the rays together.

Why did you draw the lens so big? It should be smaller than the book.

An infinite number of rays leave every point on the object. As you can see from the drawing below for the top of the arrow, all of the rays from a single point that go through the lens also converge at a single point. Therefore, it doesn't matter which rays we draw--any rays will show us the point of convergence. The principle rays have simple rules that allow us to know their outgoing directions, and so we draw the lens big enough to encompass them. Even if those three rays don't actually go through the lens, they show us where the rays that do go through the lens converge.

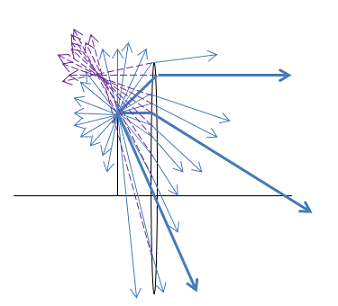
You talk about drawing light from the object to your eye, and yet none of the principle rays that you drew went to the eye. How do you see the image?

The answer to this question is the same as the answer to the previous question. There is an infinite number of rays that leave the object and all converge at the same (image) location. You can see in the drawing that at subset of those rays will get to your eye, and they converge in the same place that the principle rays converge.

It is conventional to represent any object for an optics problem with an arrow. The reason for this is simple. As long as you know where any two points of the object appear to be, you can locate the entire image. The arrow shows a definite top and so it is a simple shape that allows you to distinguish between upright and inverted images and therefore contains all of the information that you need about the object.

It is also conventional to draw the bottom of the arrow on the optical axis. This does not necessarily mean is it the bottom of the object, just another point on the object. But the optic axis is an easy point to track--because rays along the optic axis strike the interface with the lens perpendicular to its surface, they do not change direction. Therefore, the corresponding point on the image is also on the optic axis.

Take a look at the drawings. From your perspective, the lens is above, or in front of, the book. In the case of a magnifying glass, you also know that the lens is close enough to the object that the object is within the focal distance. If you did not know this result from memory, you would quickly catch your error when you drew principle rays for an object outside the focal point, as you would end up with an inverted image.

Because all rays from a single point on the object are focused to a single point on the image, you actually only need two principle rays. However, drawing three will help you to catch errors.

Note that the definition of focal point is the point at which a ray initally traveling parallel to the axis crosses that axis. Note also that there are two focal points for lenses. For a convex lens, rays go out through the focal point on the far side of the lens (from the object.) You can always check yourself if you don't remember for sure. In air, a convex lens acts to converge the rays--and so the angular separation between the outgoing rays should be less than the angular separation between the incident rays.

This is the most confusing principle ray to draw. Remember that you want to trace light rays that leave the object and get to your eye. A ray traveling to the left will not reach your eye--you will not see that view of the object. Therefore, it can be hard to understand how to draw a ray that goes from the object to the lens and also through the focal point.

One common mistake is to use the wrong focal point. Remember that for a convex lens, the "in" focal point is on the same side of the lens as the object, and the "out" focal point is on the far side of the lens from the object.

Another common mistake is to draw the ray going to the left as discussed above. Clearly this ray does not reach your eye. The correct approach is to draw the ray from the top of the object to the lens as if it left from the focal point. In other words, as shown by the dotted line, draw a guiding straight line that includes the "in" focal point, the top of the object, and the lens. The third principle ray originates at the top of the object but travels in that direction. Also make sure that you do not show the ray changing direction until it gets to the lens.

Note that this is just the reverse of the rule for the drawing the second principle ray. The paths of light are reversible, and so a ray that goes out parallel must be incident as if through the focal point.

The easiest, although slightly too simplistic, definition of image is that it is where your brain thinks the object is located. This definition is based on the idea that multiple rays leave every point of the object and so your brain traces the rays back straight to their apparent point of origin. (The reason this is too simplistic because our brains actually use multiple cues (such as relative size) and not only angle of light rays as they interpret what we see.)

Experience has taught your brain that light travels in straight lines.

Multiple rays of light scatter off of every point on an object. Therefore, if we trace the rays back to where they intersect, we are tracing back to their (apparent) point of origin.

You can see in the drawing that the image is larger that the object as told in the problem. In this case, that is a good double check that you drew the picture correctly. In problems where you are given both the object distance and the focal length, you can make the drawing to scale and measure the size of the image from your drawing. That was not possible here because you did not know the object distance to start.

An infinite number of rays leave every point on the object. As you can see from the drawing below for the top of the arrow, all of the rays from a single point that go through the lens also converge at a single point. Therefore, it doesn't matter which rays we draw--any rays will show us the point of convergence. The principle rays have simple rules that allow us to know their outgoing directions, and so we draw the lens big enough to encompass them. Even if those three rays don't actually go through the lens or don't actually reach your eye, they show us where the rays that do go through the lens to your eye converge.

As long as we know where any two points of the image are, we can locate the entire image. We just need to pick two points separated enough that we can tell if the image is upright or inverted. The top of the arrow may or may not be the top of the object, but it allows us to locate one image point. Our second image point is the part of the object on the optic axis. A ray coming in along the optic axis will go out along the axis, so all rays coming from that point of the object will converge on the axis. This means out of an infinite set of rays coming from every point of the object, we ultimately need to only draw three.

There are two equations that summarize our understanding of geometric optics:

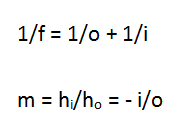
The first equation locates the image for a given lens some distance o from the object, and the second relates the size of the object to the size of the image. In this case, you are asked to relate location to size, and so you will need both equations.
- View Queries
What are o and i? My book s and s'. My book uses p and q.

In this equation, o refers to the distance between the object and the cener of the lens. i refers to the distance between the imge and the center of the lens. Some books use s and s' respectively, and others use p and q. All refer to the same understanding. I like o and i because they name the concept more directly.

o is the distance between the object (in this case, the book) and the center of the lens. When light passes from the object to the lens to your eye, o is positive. Note that this is almost always the case. Negative values for o may arise, however, in situations with multiple lenses.

m refers to magnification (not mass!) If the image is twice as big as the object, magnification is two. If the image is three times as big, it is three. If it is half as big, it is one half, etc. h_i and h_o refer to the heights of the image and object respectively.

The negative sign in this equation tells you if the image is upright (m = +) or inverted (m = -) compared to the object. Note that the statement of the equation does not mean that magnification is always negative. i is negative for a virtual image, and so (-)(-) gives a positive, or upright, image.

i is the distance between the image (where the object appears to be) and the center of the lens. When the image is between the lens and your eye, i is positive and we refer to this as a real image. When the image is on the other side of the lens as your eye, i is negative and we refer to this as a virtual image.
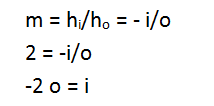
Because we know the magnification of the object, we are able to relate the distance from the object to the lens to the distance from the image to the lens. If you began instead with the 1/f equation, you would quickly see that you had two unknowns and would need to return to this equation before you could go further.

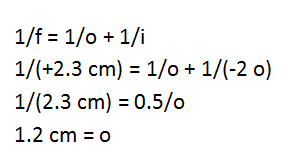
In order to magnify the letters on the book to twice their size, you need to hold the magnifying lens 1.2 cm in front of the book.
- View Queries
Do I have to go to all this work? Can't I just divide the focal length by two?

Be careful with this shortcut. You can certainly see in the magnification equation that the distance to the image is m x the distance to the object, but it is not so straightforward to work the thin lens equation in your head.

Focal length is defined as the distance from the lens at which parallel rays are focused. The sun is very far away and so its rays come in about parallel to each other, and so the focal distance is 2.3 cm. Focal length for a converging lens is positive.

Remember, o is the distance between the center of the lens and the object.

Remember, i is the distance between the center of the lens and the image.

Whether you read the question to mean that magnification is 2 or that h_i = 2 h_o, your answer is the same.

In this step, I multiplied by o and divided by -1.

In this step, I factored out 1/o. Then 1 - 1/2 = 0.5. Be careful not to take short cuts in the math.

If 1/A = 1/B + 1/C, it is not true that A = B + C!

Dividing both sides by 1/2 gives 1/o = 2/2.3 = 1/1.2. (Alternatively, 1/o = 0.87 if you use your calculator and use decimals rather than fractions.) Then taking the inverse of both sides, o = 1.2 cm.
Any time you are asked to understand what you see through a spherical lens or mirror, it is likely to be a geometric optics problem. Ray diagrams help you to visualize how the lens bends the light and how your brain understands those light rays, and also to catch mathematical mistakes. For example, note that the distance between the object and the lens is less than the focal length, as expected. If you were unsure of whether to use i = 2o or i = -2o, for example, you could catch your mistake here. In that case, make sure to understand that you need the negative (your image is upright) before you move on.