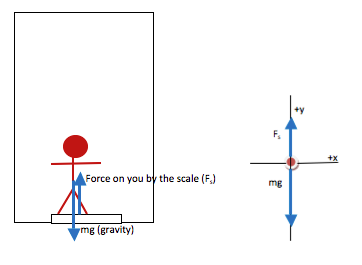
You are standing on a scale in an elevator on the 4th floor of the science building. As the elevator begins to descend to the first floor, you notice that the scale reads only 85% of your weight. What is the acceleration of the elevator during that period of time?
-
In this problem, you are asked to relate motion (the acceleration of the elevator and the objects in it) to force (your weight and the contact between you and the scale). Force and motion of a single object are always related through Newton’s Second Law, so this is a force or 2nd Law problem.
-
The free body diagram is a sketch of the forces on an object, or the causes of motion. Acceleration is the effect of those forces and therefore does not show up on the FBD. It will make an appearance in the equation.
A scale reads the amount of force that it puts on you. In this case, the scale supports you with a contact or normal force, and so the scale will read the size of that force.
Regardless of their motion, all objects near Earth experience a downward force of gravity equal to mass of the object x 9.8 m/s2.
-
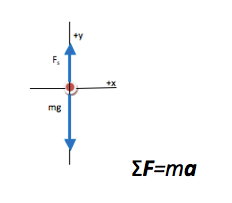
The key equation for any problem that relates forces and motion is Newton's Second Law. Regardless of what quantity you are asked to find, begin with the Second Law. If additional information is needed, it will become apparent as you proceed.
-
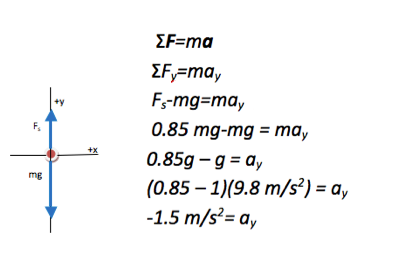
Acceleration (your acceleration is the same as the elevator’s since you move together) is the quantity that was requested in the problem and so no further mathematical steps are needed. Note that the problem would have been worked in exactly the same way if acceleration was given and the reading of the scale was requested.
Can this problem be worked using kinematics?
No. Although you are asked for acceleration you have no information about the speed of the elevator, how far it moves, or how long it takes to cover that distance. Kinematics problems focus on the description of motion (not given here) and force problems focus on the cause of that motion (gravity and the push by the scale.)
Why isn’t acceleration shown on the figure?
The free body diagram is a sketch of the forces on an object, or the causes of motion. Acceleration is the effect of those forces and therefore does not show up on the FBD. It will make an appearance in the equation.
Doesn’t a scale always read your weight?
No. A scale reads the force that it puts on you. (In the case of a bathroom scale, it reads the normal force between you and the scale; in the case of a hanging spring scale, it reads the tension in the spring.) The force that the scale puts on you depends on three things: your weight (the gravitational force on you), other forces acting on you (for example, if someone pushes on your shoulders you push harder into the scale), and your acceleration (if you and the scale were in free fall together, for example, it wouldn’t support you at all.)
Why did you choose down to be negative?
Can I pick the +y direction to be down?
Yes. In that case, mg and a would be in the +y direction, and Fs would be in the –y direction. Your answer will be the same in either case.
The problem didn’t give me any numbers. How can I solve Newton’s Second Law without knowing any values?
As long as you are confident that you correctly identified the key interactions (in this case, force) in the problem, any additional work that you need to do to deal with numbers or calculations will become apparent as you get to the point of solving the problem. Don’t worry about how you will do the calculations at this stage. The clue that it will be ok in this problem is that the two unspecified quantities are given in relative amounts to each other. That suggests that the missing information will divide out, which it does.
What happened to mass in the 5th step?
m appeared in all terms in the equation and therefore could be divided out.
Why is 9.8 m/s2 positive?
The force of gravity acts downward, which is the negative y-direction. Therefore, mg was given a negative sign in the equation. Do not also give 9.8 m/s2 a negative sign, or you will double count the direction.
My numbers are close but not exactly what is shown in the equation. Am I close enough?
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
The scale pushes up on you and therefore Fs is in the positive direction.
All forces on this object act vertically. Therefore, this is a one-dimensional problem and only needs to be solved in the y-direction.
The force of gravity acts downward, which is the negative y-direction. Therefore, mg was given a negative sign in the equation. Do not also give 9.8 m/s2 a negative sign, or you will double count the direction.
The scale exerts a force on you in the upward, or positive, direction. The magnitude of that force is 85% (0.85) of (times) your weight (mg), or 0.85 mg.
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
No. Although you are asked for acceleration you have no information about the speed of the elevator, how far it moves, or how long it takes to cover that distance. Kinematics problems focus on the description of motion (not given here) and force problems focus on the cause of that motion (gravity and the push by the scale.)
As long as you are confident that you correctly identified the key interactions (in this case, force) in the problem, any additional work that you need to do to deal with numbers or calculations will become apparent as you get to the point of solving the problem. Don’t worry about how you will do the calculations at this stage. The clue that it will be ok in this problem is that the two unspecified quantities are given in relative amounts to each other. That suggests that the missing information will divide out, which it does.
m appeared in all terms in the equation and therefore could be divided out.
Why isn’t acceleration included on the free body diagram?
The free body diagram is a stylized drawing to help you visualize the cause of acceleration, and to directly map the drawing into the left hand side (ΣF) of Newton’s Second Law. Acceleration is the effect of the forces, and therefore is not included on the list of forces themselves.
Doesn’t a properly working scale always read your weight?
No. A scale reads the force that it puts on you. (In the case of a bathroom scale, it reads the normal force between you and the scale; in the case of a hanging spring scale, it reads the tension in the spring.) The force that the scale puts on you depends on three things: your weight (the gravitational force on you), other forces acting on you (for example, if someone pushes on your shoulders you push harder into the scale), and your acceleration (if you and the scale were in free fall together, for example, it wouldn’t support you at all.)
Why doesn’t air resistance act on you?
Air resistance depends on the velocity at which you move through the air. In this case, you and the air in the elevator are moving together. You don’t move through it.
Why isn’t buoyant force included on the free body diagram?
It is true that air puts a small buoyant force on you. However, the size of the upward buoyant force compared to the downward force of gravity is very small. (The ratio of the two is given by the ratio of the density of air to the density of you.) So to the number of significant figures included in this problem, we do not need to take buoyant force into account.
Can I pick the +y direction to be down?
Yes. In that case, mg and a would be in the +y direction, and Fs would be in the –y direction. Your answer will be the same in either case.
The problem talks about what the scale reads and asks for the acceleration of the elevator. Why do you find the solution using the person?
The force that is “given” in this problem is the contact force between you and the scale, and it is true that both you and the scale feel that force equally. It is also true that you, the scale, and the elevator all experience the same acceleration. In this case, we don’t have any other information about the forces on the scale (how hard it presses into the elevator floor) or the elevator. But we do know something about the other forces (weight) on you.
-
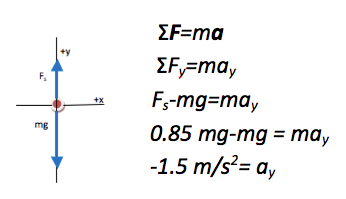
You know from experience that when an elevator first begins to move downward, you feel lighter. This is because during that initial motion, the elevator has an acceleration in the downward direction. (Note that acceleration in your solution has a negative sign, which reflects the fact that the direction is down.) This downward acceleration means the floor (or scale, in this case) does not press into you as hard because it does not fully support you against gravity. That is reflected in this problem by the fact that the force on you by the scale is only 85% or your weight.
If you were in free fall, your acceleration would be -9.8 m/s. In this case, your actual acceleration is much less than that, and so the answer appears reasonable.
- Why isn’t acceleration included on the free body diagram?
- Doesn’t a properly working scale always read your weight?
- Why doesn’t air resistance act on you?
- Why isn’t buoyant force included on the free body diagram?
- Can I pick the +y direction to be down?
- The problem talks about what the scale reads and asks for the acceleration of the elevator. Why do you find the solution using the person?