University of Wisconsin Green Bay

1. Identify the Problem (Definition)

The reason that this website has a separate section for definition problems, rather than putting them as easier problems in other sections (e.g. putting a definition of kinetic energy problem in the energy section) is because the single most important thing you should do as you begin a problem is to identify the best approach to use. Everything else that you do follows from there. Dynamics (force,) conservation of energy, kinematics (motion,) etc. problems all share a common underlying understanding and a common underlying problem-solving approach with each other.

Definition problems all have in common an essentially plug-and-chug approach. Whenever you are given one quantity and asked for a very closely related second quantity, you will approach the problem in the same way. Almost always, the two quantities are, as the category suggests, directly related through the definition of one of the quantities (e.g. density is defined as mass/volume, so mass and density are very closely linked.) A specific category in which you see this close relationship is rate questions (velocity is the rate at which displacement changes so velocity and displacement are very closely linked.)

2. Draw a Picture (Definition)

You seldom need a picture for definition equations—you tend to be told two quantities and asked for a third that is related through a single equation. Exceptions are cases in which you can’t visualize what the equation means or where it came from, or in which you are asked to look at multiple points and need to keep the given information straight. In those cases, the picture tends to be a well-labeled picture of the actual situation, rather than an abstract picture such as a free body diagram.

3. Select the Relation (Definition)

There are many, many relations that are used in definition problems. However, by the process of identifying the problem as being plug-and-chug, you will already have the relationship between your closely related variables in mind. If not, try looking in the index for the first page of your text book where the unfamiliar variable is mentioned.

4. Solve the Problem (Definition)

In most cases, you will just need to put the given information into your equation and algebraically solve for the unknown. There are several notable exceptions:

1. Average velocity: you may need to use v information in the definition of velocity equation for the legs of a trip to find x and t for each leg, and then put those values into the definition of velocity equation one more time for the trip as a whole.

2. Comparing multiple points: In some cases, you are asked to compare values at two different points. It is very common in those cases not to be given information about all of the variables. However, if you divide the definition equation at one point by the definition equation at another point, any unknown quantities that don’t change in value between the two will divide out.

5. Understand the Results (Definition)

For most definition problems, your main goal will be to become comfortable with the close relationship between the two variables—a goal that happens just by identifying the definition nature of, and relation for, the problem. However, you should stop at the end to think about the units and the size of your answer which will also add to your understanding of the variable that the problem explores.

1. Identify the Problem (Vector)

Displacement, velocity, acceleration, force, torque, angular displacement, angular velocity, angular acceleration, momentum, electric and magnetic fields are all vectors. Whenever you work with vectors that are not all along the same straight line, you need to divide the vectors into their x- and y- (and sometimes z-) components. In some cases, you will have explicit practice problems but most of the time you will work with vector components as a preliminary step to solving other problems. In the later case, it is easiest to divide the vectors into components at the "Draw a Picture" stage so that you don’t have to worry about it as you get into the problem itself.

2. Draw a Picture (Vector)

The most visual way to see the components of a vector is to draw that vector alone on your coordinate system. (It doesn’t matter if the vector quantity actually acts at the origin—you can move your coordinate system around as long as you point the axes in the same direction.) Then draw a right triangle with the vector as the hypotenuse and the sides on or parallel to the axes.

3. Select the Relation (Vector)

There are the four relations which describe a right triangle:

The last three relations are often remembered as soh-cah-toa.

If you are given a vector (the hypotenuse) and asked for components (the sides,) use the definitions of sine and cosine. The Pythagorean Theorem (Equation 1) is useful if you know the components and are asked for the vector itself.

4. Solve the Problem (Vector)

Solving vector problems and sub-problems is merely a matter of doing the math. There are three things to watch:

1. It is not true that cosine always goes with the x-axis and sine with the y-axis. It depends on which angle you use. You can always avoid mistakes by going back to the definition equations above.

2. Using this method of drawing the picture, you will need to assign + and – signs for directions of the components explicitly.

3. If you are given the components of a vector and asked for the direction, you will need to “un-do” one of the last three equations. You can do this, for example, by using the “inv tan” or “tan^-1” function on your calculator.

5. Understand the Results (Vector)

A good double check on your math is that no component is greater than the length of the vector, and that the shorter component on your triangle has a value less than the longer one. It is also a good idea to go back to the picture to make sure that you correctly assigned signs to each component.

Note that when you replace a vector with its components you have the same physical effect as for the original vector. For example, if you move either along a displacement vector or along both of its components, you will end up in the same place; if you exert a force at an angle or replace it with one force for each of its components, you will get the same acceleration.

1. Identify the Problem (Dynamics)

Any problem that asks you to relate force and motion is a Newton’s Second Law problem, no matter what was given or requested in the problem. In some cases, Newton’s Second Law is easy to identify—for example, a problem might ask you for the value of a particular force.

In other cases, it is harder to recognize 2nd Law problems. You may know forces that are present without having force ever mentioned in the problem, and you may be asked for things like how fast an object moves in a circle or how much of an object is underwater. Recognizing how to approach these problems comes from experience—taking the time to answer the question “how did I know this was a 2nd Law problem” for every single force example you work will help to build that intuition which you will need on the final exam.

2. Draw a Picture (Dynamics)

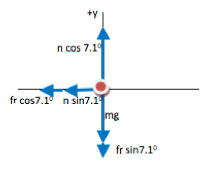
When you approach force problems, a free body diagram will allow you to both picture what is happening and directly map the picture into the equation. All the physics is done in the process of drawing the diagram—only algebra remains after this step.

The first thing that you will need to do is to identify what object(s) will be the focus of the diagram—in other words, what system do you need to consider in order to answer the question. In some cases, you will need to consider several objects as separate systems. In those cases, you will draw free body diagrams and set up equations for each object separately. You will very likely use Newton’s Third Law to relate forces on the two objects.

Once you have identified your system, think about all forces on that system, discard any that are too small to matter. Only forces acting on the object should be shown, since you are trying to understand what causes the motion of the object. The free body diagram maps directly into the left side of ∑F=ma. Acceleration is the result not the cause—if you wish to sketch the acceleration, make sure that you do so off to the side and not on the sketch of forces.

Because Newton’s Second Law is a vector equation, you will need to divide all forces into their x- and y- components in order to work with the equation. Math is always easiest if you pick one axis to be along the direction of acceleration. That way, one component of a will be zero and you will have fewer linked equations.

3. Select the Relation (Dynamics)

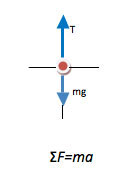All force problems begin with the relation ∑F=ma. This true no matter what you are asked to find. If any additional information is needed, it will become apparent as you work through the problem.

4. Solve the Problem (Dynamics)

∑F=ma is a vector equation and so is set up separately in the x- and directions. Think carefully about the direction of each force and include the appropriate sign. Once you have filled your forces into these equations, you have only algebra left and can solve the equations in any way that works. In general, it is easiest to solve the equation in which a=0 first as you will sometimes need those values in the other expression.

5. Understand the Results (Dynamics)

Once you have completed the problem, look at it again. Does your answer make sense? Did it give the behavior you intuitively expected to find? Can you now do steps that caused you problems earlier? Can you explain in words what is happening? If you only recognized it as a 2nd Law problem because of the section heading in your text book, identify the information that you would use to recognize a problem like this on the final exam.

1. Identify the Problem (Kinematics)

Any problem that asks you to describe the motion of an object without worrying about the cause of that motion is a kinematics problem, no matter what was given or requested in the problem. In some cases, you can use either kinematics or energy to solve a problem. However, if you are asked about time or horizontal motion you most likely will need to use kinematics.

2. Draw a Picture (Kinematics)

Because kinematic problems focus on describing motion, your picture should be a picture of the motion or path of the object of interest. Make sure to mark key points on the picture (any point about which you are given information, any point about which you are asked for information, and any point such as the top of the motion where you know information (like v_y = 0 at the top of the arc) without being explicitly told. Be careful: you do NOT know that v = 0 when an object reaches the ground. As soon as it touches the ground, there is a new force on it and the problem changes. The kinematic equations you will use are valid only up until the point where the object almost touches down.

In addition to marking key points, you should pick an origin. In other words, pick a location where x = 0 and y = 0. All other position values are then measured from that location.

Finally, kinematic variables (x, v, and a) are vectors, and so you will only be able to work with the equations one direction at a time. It is very easy to forget to work with the correct component while you are in the middle of the problem, so taking a few minutes to divide all vectors into components and organize them in a table will save a lot of mistakes and time in the long run.

3. Select the Relation (Kinematics)

There are three key kinematic equations. If you carefully select the equation which most directly describes the situation in your problem, you will not only solve the problem in fewer steps but also understand it better. The three equations, written for motion in the x-direction, are:

1. x = x₀ + v₀Δt + ½ a(Δt)² (relates position and time)
2. v = v₀ + aΔt (relates velocity and time)
3. v² = v₀² + 2a(Δx) (relates velocity and position)

Note that some books give more than three equations. For example, they might reproduce these equations with –g instead of a for motion in the y-direction, or combine them together into a range equation. All of those are special case equations—they are partially solved versions of these three basic equations and only work in certain situations. (The range equation, for example, is only valid if the object lands at the same height from which it was thrown.) It is far better to always start with one of the three basic equations. They always apply and are always used in the same way.

The greatest challenge in kinematic problems is picking the best equation to use to solve your problem. The way to do this is to think about which answer you want. If the problem asks you for position, which position is it? If you want position at a given time, pick equation 1. If you want position at a given velocity, pick equation 2. v₀ and a occur in all equations, and so if you are asked to solve for either of those variables you will need to identify two known quantities and select the equation that relates them.

4. Solve the Problem (Kinematics)

The kinematic equations are vector equations and so must be solved in the x- and y-directions separately. For many problems, you will only need to work in one dimension. If you ever need to relate the two (for example if your question asks for an x-position when the object has a given y-position) you need to go through time. Use what you know to solve for time in that direction, then use time in the other direction for your desired information.

The only tricky algebra in kinematics is if you need to solve equation 1 when v₀ is not equal to zero. In that case, you will need to use the quadratic equation.

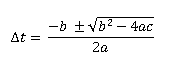
5. Understand the Results (Kinematics)

Once you have completed the problem, look at it again. Does your answer make sense? Did it give the behavior you intuitively expected to find? Can you now do steps that caused you problems earlier or do a better job identifying which equation is best to use? Can you explain in words what is happening? If you only recognized it as a kinematics problem because of the section heading in your text book, identify the information that you would use to recognize a problem like this on the final exam.

1. Identify the Problem (Energy)

Energy is never created or destroyed, although under action of a force it can change in form. Therefore, the idea of conservation of energy always applies. It is only useful for solving a problem, however, when you have enough information to track the changes in energy. You can track changes in mechanical energy (problems involving motion) if either there are no significant non-conservative forces present or if you are given adequate information about those forces.

You can also use the conservation of energy in thermal energy problems if you are asked to relate changes in thermal energy to temperature changes within, or work done by, a system.

2. Draw a Picture (Energy)

Mechanical energy problems ask you to relate the speed of your system at different positions. Therefore, the most useful picture is a sketch of the actual motion, with all known speed and position information labeled.

For thermal energy problems, changes take place in properties that can’t be drawn well (such as temperature) and so a picture is not always relevant to organize the information.

3. Select the Relation (Energy)

There are two ways to begin a mechanical energy problem. The first is to begin with the equation

KE₁ + PE₁ = KE₂ + PE₂ - W_nc

and to fill into all relevant terms. You can also begin with an energy chain (track the energy throughout the problem) and write a term in your equation for each term in the chain. You will arrive at the same results.

For thermal energy problems, you will often begin with Conservation of Energy stated as

ΔQ = ΔU + W

although, again, an energy chain may be useful (especially for problems in which you look at thermal energy going from one part of the system to another.)

4. Solve the Problem (Energy)

Once you have drawn your picture and selected your relation, solving a Conservation of Energy problem is merely a matter of doing algebra. Energy is not a vector, although signs do carry meaning and so cannot be ignored.

5. Understand the Results (Energy)

The best way to understand what is happening in an energy problem is to draw an energy chain. Start with the form(s) of energy at the initial point in the problem, and track that energy at each subsequent point of interest. Make sure to use arrows to the side to show energy leaving the system. You can then relate that chain both to a narrative of the problem and to the equation that you have after all zeros have been filled in. As always, make sure that your answer makes physical sense.

1. Identify the Problem (Momentum)

As a quick rule of thumb, if your problem involves the collision of two objects, or the separation of one system into parts, then the momentum of the combined system of all objects or parts is conserved over the time of the collision or separation.

The physics behind this rule of thumb comes directly from Newton’s Second Law. From the 2nd Law, you can see that change in momentum (Δp) is equal to F_netΔt. So if the net force on a system is zero, or small enough that F_netΔt ≈ 0 for the time period of interest, then Δp ≈ 0 and momentum is conserved. A collision or separation tends to take place over a very short time interval, so for smaller forces like friction and gravity FΔt ≈ 0 is usually true. The force involved in the collision or separation itself, however, is large. That force cancels out (Newton’s Third Law) for the system as a whole, but of course each piece feels the force and has a usually significant change in its momentum.

2. Draw a Picture (Momentum)

In Conservation of Momentum problems, you compare momentum (mv) of a system before and after a collision or separation. Therefore, you want to draw a picture of the system just before the interaction and another picture just after the interaction. Label m and v information for both. Because velocity is a vector, make sure to indicate the direction of motion as well as the speed.

3. Select the Relation (Momentum)

All Conservation of Momentum problems are understood by;

p_{system before the interaction} = p_{system after the interaction}

Momentum terms need to be included for each piece of the system and signs are given by the direction of velocity.

4. Solve the Problem (Momentum)

In many cases, collisions are one dimensional and so solving the problem is just a matter of algebra as long as you have carefully put in the signs of velocity. For two dimensional problems, you need to divide momenta into their x- and y-components and solve each equation separately.

5. Understand the Results (Momentum)

You can best understand momentum problems by tracking the momentum. Which objects sped up? Where did that momentum come from? Which slowed down? Where did it go?

E&M Problems

In many cases, problems that come under Electricity and Magnetism chapters are problems you already know how to solve. These categories include Definition problems, Dynamics (force) problems, and Conservation of Energy problems. Circuit and induction problems, however, are unique to Electricity and Magnetism.

1. Identify the Problem (Circuit)

Circuit problems are very straightforward to identify. You will be given a picture or description of a combination of resistors or capacitors and asked to find the current through (or charge on) each. (Note that if you are given information about the material out of which a resistor or capacitor if made, you have a definition problem rather than a circuit problem.)

2. Draw a Picture (Circuit)

The initial picture of the circuit is typically provided for you. However, unless you choose to use Kirchhoff’s Laws, you will need to draw a series of pictures to reduce the circuit to a single resistor (or capacitor.) Once you know this equivalent resistance (capacitance) for the entire circuit, you can find the overall effect of the battery and begin solving the problem.

The key in circuit problems is to draw enough pictures, so that in any one step you can clearly see how that picture is a reduced version of the previous picture. If you draw the increasingly simple pictures going down the left side of your paper, this leaves you room to work each sub-problem to the right and work your way back up to the original circuit.

To draw useful pictures, look at your current drawing and select the “innermost” combination of elements to reduce. For example, there might be resistors in series within a parallel combination. You must reduce the series of resistors before you can reduce the parallel piece. As you go from picture to picture, make sure to use the equations for equivalent resistance or capacitance to put in the correct value on your new picture.

3. Select the Relation (Circuit)

Circuits of resistors are understood with ΔV = IR. Circuits of capacitors are understood through ΔV = Q/C.

4. Solve the Problem (Circuit)

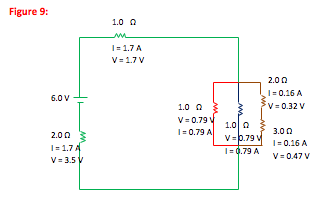You can use the voltage gain by the battery and the equivalent resistance (or capacitance) of the circuit to find I or Q in your simplest drawing. Then remember that current is the same for resistors in series and voltage drop is the same across resistors in parallel to work up to the more complicated drawings. Any voltage drop that you find across a “combined” parallel resistor is the same as the voltage drop across the individual resistors, allowing you to now solve for current across each. Likewise, any current you find for a “combined” series resistor is the same as the current through each of the individual resistors, allowing you to solve for voltage drop across each. Record keeping is important—any time you solve for a value, write it in on all relevant drawings.

5. Understand the Results (Circuit)

The key ideas that you use when you work circuit problems are Conservation of Charge and Conservation of Energy.

Conservation of Charge tells you that electrons are not used up in resistors—they merely give up some of their electric potential energy. Therefore, you can trace the path of the current in a circuit. Any region of the circuit for which there is no alternate path must have the same current, and when there are alternate paths the current in each must add up to the total.

Conservation of Energy tells you that in the steady state of the circuit, electrons gain the same amount of potential energy as they go through the battery as the total they lose going across all resistors in their path. Therefore, as you follow any path in the circuit, you will find that that voltage gains balance the voltage drops.

1. Identify the Problem (Induction)

Any time you are asked about EMF or current in a loop (real or imagined), you have electromagnetic induction during any period of time in which the amount of magnetic flux through the loop changes. If there is no change, there is no induction.

2. Draw a Picture (Induction)

Effective pictures for induction problems show the loop(s), the magnetic field, their relative orientation, and indicate in some way what is causing the flux to change. Because these problems are typically three-dimensional, “X”s are used to indicate any vector pointing into the paper, and “ ∙ “s are used to indicate vectors pointing out of the paper.

3. Select the Relation (Induction)

All induction problems are understood through the relation
EMF = -N ΔΦ/Δt = -N Δ(BA cosθ)/Δt.

If you are asked to find induced current, you will also need to use EMF = IR.

Direction of induced current is such that the induced magnetic field due to that induced current opposes the change in the original magnetic flux.

4. Solve the Problem (Induction)

Typically, magnetic flux through a loop changes because either the magnetic field or the size of the loop or the orientation of the loop changes. Leave that changing quantity inside the Δ (remember, this means final value – initial value) and the math is generally straightforward to solve.

You should relate the direction of the induced current to that of the induced magnetic field through the 2-step right hand rule.

5. Understand the Results (Induction)

Remember that you only have induction if the magnetic flux through a loop changes. Take a look at your problem and identify the source of the magnetic flux. Then identify what happens to cause that flux to change. Your math in solving the EMF equation should directly pair with the cause of the change in flux. If you have a closed loop, the induced EMF will result in a current through the loop, just as a battery would.