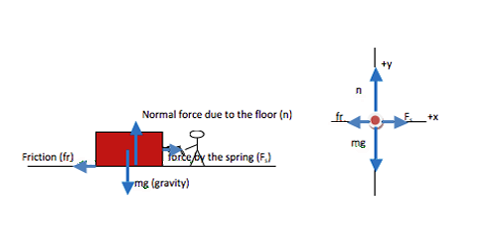
For no apparent reason, you decide to pull a heavy box of books across the floor using a spring. When you get the box moving at a constant velocity, the spring is stretched 0.10 m past its relaxed length. If the box has a mass of 35 kg and if the coefficient of friction between the box and the floor is 0.43, what is the spring constant of the spring? Assume that you pull the spring parallel to the floor.
Hint: The free body diagram and approach to solving the problem are exactly the same as if you push the box directly, or pull it with a rope. Don’t let the spring deter you from using this example with a simpler problem.
-
In this problem, you are provided information about the motion of an object (the box moves at constant velocity) and about the forces causing that motion (the pull by the spring and friction.) Force and motion of a single object are always related through Newton’s Second Law, so this is a force or 2nd Law problem.
-
How does the spring affect how I work the problem?
It doesn’t! Whether you push or pull the box directly or with a spring, you set up the problem in exactly the same way. The only difference will be in the algebra of the problem—which variable you solve for.
Why isn’t acceleration shown on the figure?
The free body diagram is a sketch of the forces on an object, or the causes of motion. Acceleration is the effect of those forces and therefore does not show up on the FBD. It will make an appearance in the equation.
I am pulling the box. Why doesn’t a force by me show up on the FBD?
Do not include a force by you on the box. It is true that you are pulling it, but you do so through the spring. The box has the same motion regardless of what stretches the spring. If you also include a force by you, you will double count your affect on the box’s motion.
How does the fact that the box moves at constant velocity affect the FBD?
If velocity is constant, acceleration is 0. Acceleration does not show up on the FBD, but this information will be useful later in the solution.
I’m asked to find the spring constant rather than a force. How does that affect my picture?
The spring force always acts in the direction needed to restore the spring to its original length. In this case, you stretched the spring, so the left end pulls toward the right and the spring force in the box is to the right.
The magnitude of the spring force is given by |kx|, where k is the spring constant and x is the amount that the spring is stretched (or compressed) from its relaxed length.How do you know what to fill in for x?
In the definition of spring force, x is used to represent the amount the spring is stretched or compressed. In this case, it is stretched 0.10 m.
How do you know what to fill in for acceleration?
The box moves at a constant velocity and so its acceleration is zero.
Why is 9.8 m/s2 positive?
The force of gravity acts downward, which is the negative y-direction. Therefore, mg is given a negative sign in the equation. Do not also give 9.8 m/s2 a negative sign, or you will double count the direction.
My numbers are close but not exactly what is shown in the equation. Am I close enough?
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
If velocity is constant, acceleration is 0. Acceleration does not show up on the FBD, but this information will be useful later in the solution.
The spring force always acts in the direction needed to restore the spring to its original length. In this case, you stretched the spring, so the left end pulls toward the right and the spring force in the box is to the right.
The magnitude of the spring force is given by |kx|, where k is the spring constant and x is the amount that the spring is stretched (or compressed) from its relaxed length.All objects near Earth experience a downward force of gravity equal to mass of the object x 9.8 m/s2.
Friction always opposes the sliding motion of two surfaces across each other. Because the box slides forward across the floor, the friction of the floor pulls backward on the box.
Normal force is present whenever two surfaces are in contact with each other. Its direction is perpendicular to the surfaces and acts to keep them from falling through each other. In this case, the upward normal force from the floor prevents the box from falling downward through the floor.
Do not include a force by you on the box. It is true that you are pulling it, but you do so through the spring. The box has the same motion regardless of what stretches the spring. If you also include a force by you, you will double count your affect on the box’s motion.
Why isn’t acceleration included on the free body diagram?
The free body diagram is a stylized drawing to help you visualize the cause of acceleration, and to directly map the drawing into the left hand side (ΣF) of Newton’s Second Law. Acceleration is the effect of the forces, and therefore is not included on the list of forces.
The problem asks for the spring constant of the spring. Why did you focus the free body diagram on the box rather than the spring?
The spring pulls back on the box with the same force that the box pulls on the spring. You can therefore learn about the spring force by looking at either object. However, Newton’s Second Law requires you to include all significant forces on whatever system you pick. In this case, you don’t know how hard you are pulling on the spring and so do not have the necessary information to examine the problem from the perspective of the spring.
You, the box, and the spring all move together. Why don’t you include all three objects as a single system for analyzing in this problem?
In this case, you are asked a question that requires knowing the force exerted by the spring. If you take all objects together as a single system, that force is internal to the system and won’t show up in your analysis (any more than, for example, intermolecular forces within the box need to be taken into account.)
Why isn’t there air resistance?
There is! However, air resistance depends on velocity (squared) as well as on cross sectional area, and so at low speeds (pulling a heavy box of books) it is much smaller than the other forces on the box and can therefore be ignored for the accuracy required in this problem.
Why isn’t buoyant force included on the free body diagram?
It is true that air puts a small buoyant force on the box. However, the size of the upward buoyant force compared to the downward force of gravity is very small. (The ratio of the two is given by the ratio of the density of air to the density of the box of books.) So to the number of significant figures included in this problem, we do not need to take buoyant force into account.
-
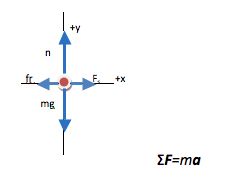
The key equation for any problem that relates forces and motion is Newton’s Second Law. Regardless of what quantity you are asked to find, begin with the Second Law. If additional information is needed, it will become apparent as you proceed.
In this case, you are not asked for either a force or acceleration, but rather for a quantity that is related to a force. That does not affect how you solve the problem. The key interaction is force, and details of what you are asked to find don’t show up until the final algebraic steps.
-
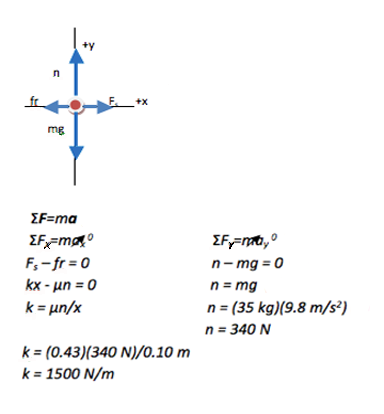
It doesn’t matter whether you start with the x- or the y- equation. If you begin with the x- equation, you will find that you need to solve the y- equation for normal force before you can complete the solution, so you are steered to the information you need regardless of where you begin.
Spring constant, or k, is the quantity that was requested in the problem and so no further mathematical steps are needed. Note that it isn’t until you fill in definitions for the forces (gravity = mg, friction = µn, spring force = kx) that you need to think at all about which information is given and what you are asked to find.
Normal force is upward and therefore in the positive y direction. It is a passive force (its value depends on the other forces present) and so does not have an equation to define it.
The force of gravity acts downward, which is the negative y-direction. Therefore, mg is given a negative sign in the equation. Do not also give 9.8 m/s2 a negative sign, or you will double count the direction.
The box moves at a constant velocity and so its acceleration is zero.
The spring force always acts in the direction needed to restore the spring to its original length. In this case, you stretched the spring, so the left end pulls toward the right or the +x direction.
The magnitude of the spring force is given by |kx|, where k is the spring constant and x is the amount that the spring is stretched from its relaxed length, 0.10 m.Friction always opposes the sliding motion of two surfaces across each other. Because the box slides forward across the floor, the friction of the floor pulls backward on the box which is the –x direction. The magnitude of sliding friction is given by µn.
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
-
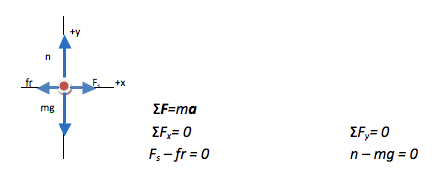
In this problem, the box travels at a constant velocity in the x-direction. This means that the horizontal forces pulling to the right (the spring force) exactly balance the horizontal forces pulling to the left (friction.) Remember Newton’s First Law: when the net force on an object is zero, the velocity of that object doesn’t change. This seems counter-intuitive. In your experience, you always need to provide a force to keep an object moving—because you need to balance the force of friction that acts against it.
In the y-direction, the velocity of the box is also constant (the box remains at rest.) Therefore, the upward normal force from the floor exactly balances the downward pull of gravity.
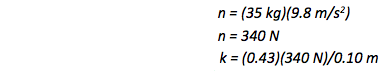
The algebraic process that you use in this problem to arrive at a numerical solution is one that you will use over and over again: solve Newton’s Second Law in the y-direction to find normal force, and then use the normal force to calculate frictional force which acts in the x-direction.
- Why isn’t acceleration included on the free body diagram?
- The problem asks for the spring constant of the spring. Why did you focus the free body diagram on the box rather than the spring?
- You, the box, and the spring all move together. Why don’t you include all three objects as a single system for analyzing in this problem?
- Why isn’t there air resistance?
- Why isn’t buoyant force included on the free body diagram?