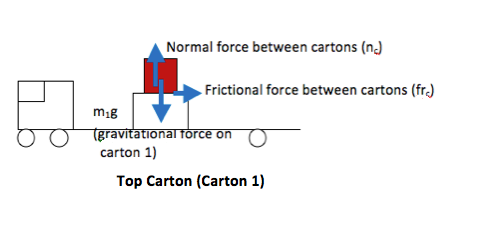
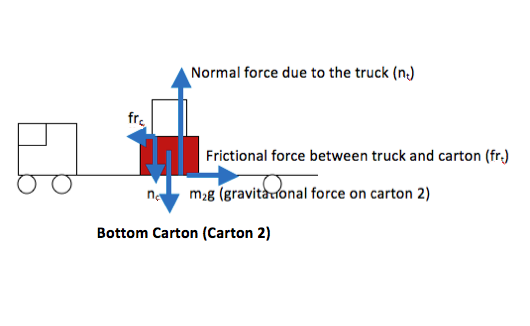
A delivery truck with two stacked cartons in the back brakes quickly. The carton on the bottom just barely stays put on the floor of the truck. Does the top carton stay put or does it fall off? The top carton has a mass of 27 kg and the mass of the bottom carton is 22 kg. The coefficient of static friction between the bottom carton and the truck is 0.42, and the coefficient of kinetic friction for that surface is 0.35. The coefficient of static friction between the cartons is 0.40, and the coefficient of kinetic friction is 0.32.
-
In this problem, you are asked to relate motion (of the cartons) to force (the friction between them). Force and motion of a single object are always related through Newton’s Second Law, so this is a force or 2nd Law problem.
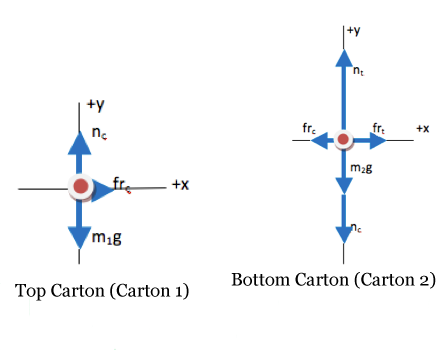
In addition, note that you must treat the two cartons as separate systems. You don’t know if they move together as a single unit or not, and cannot answer that question without examining the forces between them. Therefore, you will need to draw a picture and set up equations for each carton individually.
-
Do I have to go through all this work? The coefficient of friction on the top carton is less than that on the bottom carton, so I already know it won’t stay in place.
It is true that you can do this problem by thinking carefully about all the forces but without all of the math steps. Do notice that there is a forward force on the lower carton in addition to the frictional force acting backwards on it, and so you do need to justify to yourself that it doesn’t affect that answer. Regardless, this problem is provided as a sample because it illustrates how you would apply Newton’s 2nd and 3rd Law in a wide variety of problems that you might be asked to solve on your homework, and so it is worth looking at the mathematical analysis.
What makes the top carton move forward?
Inertia. At the start of the problem, the truck and both cartons are traveling forward. As the truck brakes, each carton will continue to move forward at a constant velocity due to inertia unless there is a net force (such as friction) acting on it. There is no forward force on the top carton.
Why is frc forward on the bottom carton?
The problem statement tells you that there is friction both between the bottom carton and the truck and between the two cartons. Recall that friction acts to oppose sliding motion. As the truck slows down, the bottom carton wants to slide forward (continue at a constant velocity) so the friction that the truck puts on the bottom carton (frt) is backwards.
Similarly, the top carton wants to slide forward across the bottom one (which is slowing down with the truck.) Therefore, friction between the cartons (frc) opposes a motion in which the top carton slides forward relative to the bottom (friction on the top carton is directed backwards) and the bottom carton slides backward with respect to the top (friction on the bottom carton is directed forward.) A good analogy for friction is Velcro—if the bottom tape pulls backward on the top tape, the top tape pulls forward on the bottom one. I used the same symbol for this force (frc) on both free body diagrams, because both cartons feel the strength of the interaction equally (Newton’s Third Law.)Why didn’t you include the weight of the top carton in the FBD of the bottom carton?
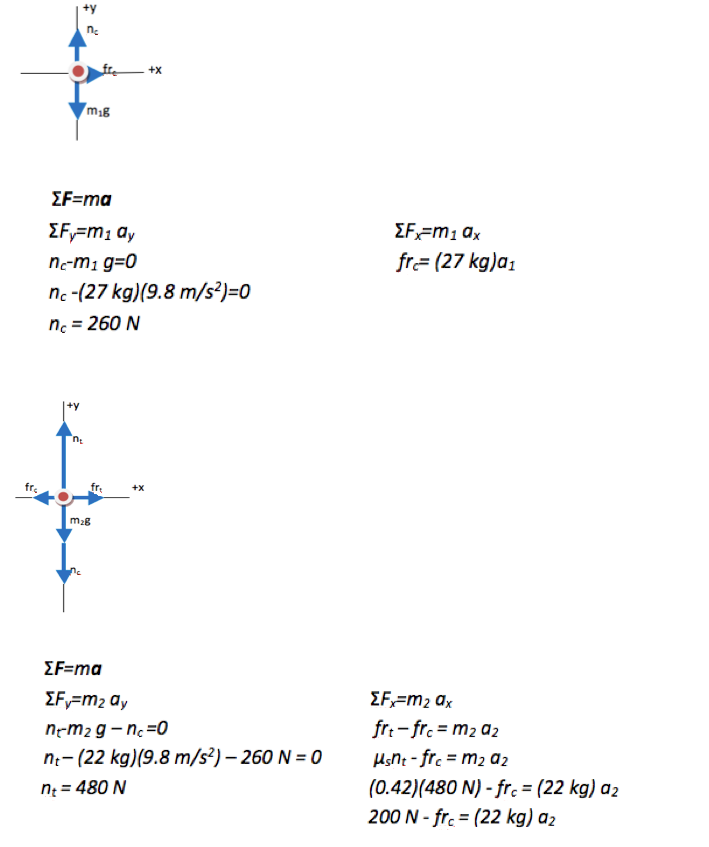
The gravitational force on the bottom carton is due to its mass only. It is true that the bottom carton feels the weight of the top carton. However, that information is transmitted through the force of contact, nc.
Why don’t you show a braking force on the cartons?
Braking acts to slow an object, so acceleration of the truck and the cartons is in the opposite direction as the velocity. The braking force acts directly on the truck and is transmitted to the cartons through friction. If you include a force by the brakes in your FBDs for the cartons, you will double count the retarding force.
Why isn’t acceleration included on the FBDs?
The free body diagram is a sketch of the forces on an object, or the causes of motion. Acceleration is the effect of those forces and therefore does not show up on the FBD. It will make an appearance in the equation.
Why is 9.8 m/s2 positive?
The force of gravity acts downward, which is the negative y-direction. Therefore, mg is given a negative sign in the equation. Do not also give 9.8 m/s2 a negative sign, or you will double count the direction.
My numbers are close but not exactly what is shown in the equation. Am I close enough?
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
Braking acts to slow an object, so acceleration of the truck and the cartons is in the opposite direction as the velocity. The braking force acts directly on the truck and is transmitted to the cartons through friction. If you include a force by the brakes in your FBDs for the cartons, you will double count the retarding force.
The problem statement tells you that there is friction both between the bottom carton and the truck and between the two cartons. Recall that friction acts to oppose sliding motion. As the truck slows down, the bottom carton wants to slide forward (continue at a constant velocity) so the friction that the truck puts on the bottom carton (frt) is backwards.
Similarly, the top carton wants to slide forward across the bottom one (which is slowing down with the truck.) Therefore, friction between the cartons (frc) opposes a motion in which the top carton slides forward relative to the bottom (friction on the top carton is directed backwards) and the bottom carton slides backward with respect to the top (friction on the bottom carton is directed forward.) A good analogy for friction is Velcro—if the bottom tape pulls backward on the top tape, the top tape pulls forward on the bottom one. I used the same symbol for this force (frc) on both free body diagrams, because both cartons feel the strength of the interaction equally (Newton’s Third Law.)The two cartons press against each other. In other words, there is a normal force between the cartons. As understood through Newton’s Third Law, both cartons feel that interaction equally and so I used the same symbol for the force on both FBDs. The bottom carton pushes up against the top carton, and the top carton pushes down against the bottom one.
The gravitational force on the bottom carton is due to its mass only. It is true that the bottom carton feels the weight of the top carton. However, that information is transmitted through the force of contact, nc.
-
The key equation for any problem that relates forces and motion is Newton’s Second Law. Regardless of what quantity you are asked to find, begin with the Second Law. If additional information is needed, it will become apparent as you proceed.
For multiple object problems, you will always need the additional information summarized as Newton’s Third Law (the interaction between two objects is felt by both objects equally and in the opposite direction.) In this example, that understanding has already been used—the contact force between the cartons was given the same symbol for each, and the frictional force between the cartons was given the same symbol for each. If you did not recognize the Third Law as you drew the FBDs, that is ok. When you start to solve the equations, you will find that you have too many unknowns and you can use the Third Law to reduce them at that point.
-
Step 1
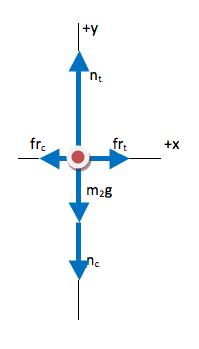
One of the keys to successfully solving a multi-object problem algebraically is to keep track of the variables. I used different symbols for the masses of the two cartons because they are not the same, and I used different symbols for the accelerations of the cartons because we do not know if they move together or not. I used the same symbols for forces that are of equal strength (Third Law pairs.) If you did not recognize the Third Law pairs when you drew the FBDs, this would be the time to note and include that information.
Most two object problems would be algebraically solvable in this step. However, in this case we have three unknowns (a1, a2, and frc) and only two equations. Continue down to step 2 of this problem.
----------------------------------------------------------------------------------------------
Step 2
In this problem, we have three unknowns (a1, a2 and frc) and two equations:
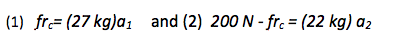
We are asked to determine if the top carton stays on top of the bottom carton. We know conceptually that it does if the force of friction is great enough to provide the same acceleration that the bottom carton experiences. So the simplest solution is to assume that the boxes move together, in other words, that
a1 = a2 = a
and to compare the force of friction required to the maximum friction that is possible between the two boxes. When solving multiple equations in multiple unknowns, you can always solve one equation for one of the variables (I will solve equation (1) for a) and substitute it into the other equation.

So, again, it would require a frictional force of 110 N between the two cartons in order for the top carton to stay on top of the bottom one. The force of static friction between the two cartons is
frstatic ≤ µsn
frstatic ≤ (0.40)(260 N)
frstatic ≤ 100 N (so friction is not strong enough to keep the top carton on top of the bottom and it will slide off)
Static friction is a passive force. In other words, it has a maximum value (frstatic ≤ µsn) but up to that maximum its actual value depends on the motion and other forces present. When problems use words like “barely” or “just” they are typically referring to the point at which friction is at its maximum. In this case, if the acceleration were any greater, the carton would slide—the force of static friction is as large as it can be. Therefore, we know the value of static friction is its maximum: µsn. This is the force between the bottom carton and the truck, so the appropriate normal force is nt.
Static friction is a passive force. In other words, it has a maximum value (frstatic ≤ µsn) but up to that maximum its actual value depends on the motion and other forces present. In this case, we don’t know if static friction on the top carton is at its maximum value or not, and so we can’t fill in an equation for it.
The bottom carton feels the weight of the upper carton through the normal force, nc. Don’t double count the weight by including m1 in the gravitational force.
The force of gravity acts downward, which is the negative y-direction. Therefore, mg is given a negative sign in the equation. Do not also give 9.8 m/s2 a negative sign, or you will double count the direction.
Newton’s Second Law is used for each carton individually. Subscripts are used to keep track of the different masses and accelerations. Identical symbols should only be used for identical values.
The normal force and the frictional force in this equation refer to the same surface. The normal force between the cartons is 260 N.
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
Why isn’t acceleration included on the free body diagrams?
The free body diagram is a stylized drawing to help you visualize the cause of acceleration, and to directly map the drawing into the left hand side (ΣF) of Newton’s Second Law. Acceleration is the effect of the forces, and therefore is not included on the list of forces.
Why didn’t you treat the two cartons together as a single system?
In this case, we don’t know if the cartons move together or not. To answer that question, we need to look at the forces that they put on each other.
How do you work force problems with two objects (systems)?
You follow the same procedure as you do for a single system problem, but do it for each object. In other words, for this problem you will need to make two free body diagrams and set up two sets of equations. In addition, recognize that all forces of interaction between the two objects are Third Law pairs. Each object feels the magnitude of the interaction equally but in the opposite direction. So make sure to give the forces the same symbol on both free body diagrams to reduce the number of unknowns that you have to solve for in the final steps of the problem.
What makes the top carton move forward?
Inertia. At the start of the problem, the truck and both cartons are traveling forward. As the truck brakes, each carton will continue to move forward at a constant velocity due to inertia unless there is a net force (such as friction) acting on it. There is no forward force on the top carton.
Why is frc in the forward direction on the bottom carton?
Frictional force acts to oppose sliding motion. We know that the bottom carton slows down with the truck. The top carton will continue to move forward at a constant velocity unless friction acts to slow it down. Therefore, friction between the cartons opposes a motion in which the top carton slides forward relative to the bottom (friction on the top carton is directed backwards) and the bottom carton slides backward with respect to the top (friction on the bottom carton is directed forward.) A good analogy for friction is Velcro—if the bottom tape pulls backward on the top tape, the top tape pulls forward on the bottom one.
It is true that you can do this problem by thinking carefully about all the forces but without all of the math steps. Do notice that there is a forward force on the lower carton in addition to the frictional force acting backwards on it, and so you do need to justify to yourself that it doesn’t affect that answer. Regardless, this problem is provided as a sample because it illustrates how you would apply Newton’s 2nd and 3rd Law in a wide variety of problems that you might be asked to solve on your homework, and so it is worth looking at the mathematical analysis.
-
In this problem, you were asked to consider the motion of two cartons.
The bottom carton experiences a backward force of friction with the floor of the truck (acting against its motion) and also a forward force of friction due to the upper carton sliding across it. Because the backward friction is greater than the forward friction, the bottom carton slows down and remains in place on the floor of the truck. The amount of friction with the floor is larger than the carton would experience if it did not have another box stacked on top of it. This is seen because nt is equal to the weight of the bottom carton plus the normal force of the upper carton pushing on it.
The top carton experiences only one force of friction, acting backwards across the surface with the lower carton. The maximum value for that force of friction is 100 N. It would require a force of 110 N to hold the top carton in place on top of the bottom carton, and so it will slide off.