A 15 kg block rests on an inclined plane. The plane makes an angle of 25o with the horizontal, and the coefficient of friction between the block and the plane is 0.13. The 15 kg block is tied to a second block (mass=38 kg) which hangs over the end of the inclined plane after the rope passes over an ideal pulley. What is the acceleration of each of the two blocks, and what is the tension in the rope?
-
In this problem, you are asked to relate motion (the acceleration of the two blocks) to force (tension in the rope, friction). Force and motion of a single object are always related through Newton’s Second Law, so this is a force or 2nd Law problem.
In addition, note that you must treat the blocks as separate systems. You are asked to find the tension in the rope between them, and cannot answer that question without examining the interaction between them—in other words, the effect that each has on the other. Therefore, you will need to draw a picture and set up equations for each block individually.
-
Step 1
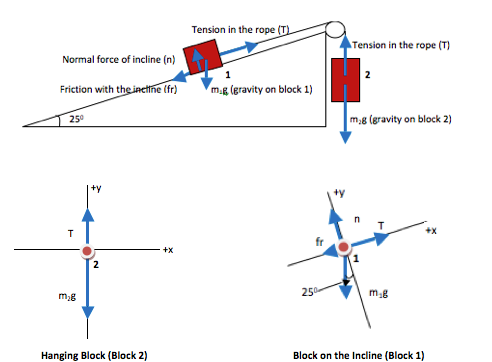
Your FBD for Block 1 is not yet finished, because mg has both x- and y- components. Continue down to step 2 when you are ready to continue.
----------------------------------------------------------------------------------------------
Step 2

In the final FBD drawn here, all forces on Block 1 are divided into components. The contribution each force makes in the x-direction (along the incline) is shown explicitly, as is the contribution each force makes in the y-direction. The FBD is now a visual representation of ∑F=ma in each direction.
Why isn’t acceleration shown on the figure?
The free body diagram is a sketch of the forces on an object, or the causes of motion. Acceleration is the effect of those forces and therefore does not show up on the FBD. It will make an appearance in the equation.
How did you know which direction to pick for friction? You aren’t told if the box slides up or down the incline.
In this problem, you are told that there is friction between Block 1 and the incline. You know that friction acts to oppose sliding motion, but you aren’t told whether the block is moving up or down the incline. I assumed that Block 1 would move up the incline, because Block 2 is significantly more massive. If I am incorrect in this assumption, my answer won’t make sense and I will need to redraw the FBD with friction acting in the other direction.
How did you know where to put the 25oangle?
There are two ways to approach this question. If you think visually, exaggerate the small and large angles on your drawing. In other words, 25o is less than half of a right angle, so draw the slope of the incline to be very small. Then you can see that mg makes a smaller angle with the –y axis than it does with the -x axis, and the smaller angle is 25o.
If you think geometrically, use the fact that the two small angles on a right triangle add up to 90o. The triangle on the first drawing made by the ground, the incline, and mg is a right triangle, so the angle between the incline (the -x axis) and mg must be (90-25)o=65o. It is equally fine to use the 65o angle, just note that sin and cos are reversed (because which side is opposite and which is adjacent depends on the triangle you draw.) You will get the same answer because sin(65o)=cos(25o).
I chose to use the first method simply because that is an easier way to determine the correct angle for most students.
Why did you choose different coordinate systems for the blocks?
The math is always easier if you pick one of your axes along the direction of acceleration. That way, acceleration only has one component and you have fewer linked equations. In this case, Block 2 accelerates downward and Block 1 accelerates along the incline, and so the y-axis for Block 2 was chosen downward and the x-axis for Block 1 was chosen along the incline. If you chose a horizontal/vertical
Why did you use the same symbol for tension on the two different blocks? Won’t that confuse you when you solve the equations?
Tension is the result of the molecular attractions in a rope, holding the rope together. Therefore, it always acts toward the center of a rope. In this case, you have the same rope acting on both blocks, so the magnitude of the tension is the same on each (even though the pulley has changed the direction.) Therefore, I used the same symbol for tension in each FBD—it is a single unknown and not two different values.
Why didn’t you include any forces from the pulley?
The problem stated you have in “ideal pulley.” This is a pulley that is light enough and has low enough friction that you can neglect any effect it has on the tension in the rope. It changes the rope’s direction, but does not affect the magnitude of tension.
How did you divide gravity into its components?

As you can see in the figure, the x- and y-components of a vector make up the sides of a right triangle. The vector itself forms the hypotenuse (h). The side of the triangle opposite the angle that you use is given by h sinθ and the side that touches the angle you use is given by h cosθ (soh cah toa)
In this case, the x-component is opposite to the 25o angle and adjacent to the 65oangle, and so can be given by mg sin(25o) as shown, or by mg cos(65o) if you chose to use that angle instead. Likewise, the y-component is adjacent to the 250 angle and is therefore given by mg cos(25o).
Isn’t the x-component always cosθ and the y-component always sinθ?
No. Cosine goes with the component that is adjacent to θ, and sine goes with the component that is opposite to θ.

The free body diagram is a sketch of the forces on an object, or the causes of motion. Acceleration is the effect of those forces and therefore does not show up on the FBD. It will make an appearance in the equation.
Tension is the result of the molecular attractions in a rope, holding the rope together. Therefore, it always acts toward the center of a rope. In this case, you have the same rope acting on both blocks, so the magnitude of the tension is the same on each (even though the pulley has changed the direction.) Therefore, I used the same symbol for tension in each FBD—it is a single unknown and not two different values.
The problem stated you have in “ideal pulley.” This is a pulley that is light enough and has low enough friction that you can neglect any effect it has on the tension in the rope. It changes the rope’s direction, but does not affect the magnitude of tension.
In this problem, you are told that there is friction between Block 1 and the incline. You know that friction acts to oppose sliding motion, but you aren’t told whether the block is moving up or down the incline. I assumed that Block 1 would move up the incline, because Block 2 is significantly more massive. If I am incorrect in this assumption, my answer won’t make sense and I will need to redraw the FBD with friction acting in the other direction.
There are two ways to know where to put the 25o angle on your FBD. If you think visually, exaggerate the small and large angles on your drawing. In other words, 250 is less than half of a right angle, so draw the slope of the incline to be very small. Then you can see that mg makes a smaller angle with the –y axis than it does with the -x axis, and the smaller angle is 25o.
If you think geometrically, use the fact that the two small angles on a right triangle add up to 90o. The triangle on the first drawing made by the ground, the incline, and mg is a right triangle, so the angle between the incline (the -x axis) and mg must be (90-25)o. It is equally fine to use the 65o angle that mg makes with the -x axis.The math is always easier if you pick one of your axes along the direction of acceleration. That way, acceleration only has one component and you have fewer linked equations. In this case, Block 2 accelerates downward and Block 1 accelerates along the incline, and so the y-axis for Block 2 was chosen downward and the x-axis for Block 1 was chosen along the incline. If you chose a horizontal/vertical coordinate system for Block 1, a1 would have both x- and y-components and you would end up having three linked equations in three unknowns instead of two when it is time to solve the problem.

As you can see in the figure, the x- and y-components of a vector make up the sides of a right triangle. The vector itself forms the hypotenuse (h). The side of the triangle opposite the angle that you use is given by h sinθ and the side that touches the angle you use is given by h cosθ (soh cah toa)
In this case, the x-component is opposite to the 25o angle and adjacent to the 65oangle, and so can be given by mg sin(25o) as shown, or by mg cos(65o) if you chose to use that angle instead. Likewise, the y-component is adjacent to the 250 angle and is therefore given by mg cos(25o).
-
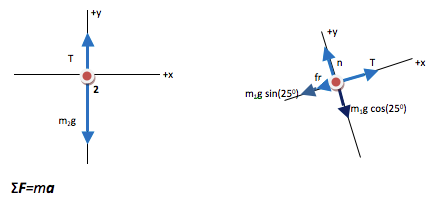
The key equation for any problem that relates forces and motion is Newton’s Second Law. Regardless of what quantity you are asked to find, begin with the Second Law. If additional information is needed, it will become apparent as you proceed.
For multiple object problems, you will always need the additional information summarized as Newton’s Third Law (the interaction between two objects is felt by both objects equally and in the opposite direction.) In this example, that understanding has already been used—the interaction between the two blocks comes through tension in the rope, and tension was given the same symbol for each. If you did not recognize that tension is the same throughout the rope as you drew the FBDs, that is ok. When you start to solve the equations, you will find that you have too many unknowns and you can use this understanding to reduce them at that point.
-
Step 1

One of the keys to successfully solving a multi-object problem algebraically is to keep track of the variables. I used different symbols for the masses of the two blocks because they are not the same, but I used the same symbol for acceleration because they move together. I also used the same symbol for tension on each block.
At this point, you have two unsolved equations and two unknowns (a and T.). Scroll down to continue this solution.
----------------------------------------------------------------------------------------------
Step 2
At this stage in the problem, we have two unknowns, a and T, and two unsolved equations:
T – 370 N = -(38 kg)a
T – 79 N = (15 kg) a
One approach that always works is to solve one equation for one of the variables and substitute it into the other.
T = 370 N – (38 kg)a from the first equation
370 N – (38 kg)a - 79 N = (15 kg) a substituting into the second
290 N = (38 kg + 15 kg)a
5.5 m/s2=a
Now that you have solved for one of the unknown variables, substitute it into either of the original equations to solve for the other variable. I will substitute it into the second equation.
T – 79 N = (15 kg)(5.5 m/s2)
T = 79 N + 83 N = 160 N
Tension in the rope and acceleration of the blocks are the only information requested in this problem. No further mathematical solution is necessary.
Why is 9.8 m/s2 positive?
The force of gravity acts downward, which is the negative y-direction. Therefore, mg is given a negative sign in the equations. Do not also give 9.8 m/s2 a negative sign, or you will double count the direction.
My numbers are close but not exactly what is shown in the equation. Am I close enough?
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
Why did you use the same symbol, but opposite signs, for acceleration of the two blocks?
The two blocks in this problem are connected together and so have the same value (magnitude) for acceleration. Therefore, I used the same symbol for the acceleration of each. For Block 1, this acceleration is up the incline, or in the +x direction. For Block 2, the acceleration is downward, or in the –y direction. “a” as the unknown quantity here is for the magnitude of the acceleration. I have used direction information in understanding that the objects move together, and therefore I must also put direction information into the equations as the sign of the a vector.
Isn’t normal force on Block 1 equal to its weight of 150 N?
Normal force on Block 1 is not the same as the gravitational force on Block 1 because the block is on an incline. Gravity pulls straight down—the y-component of gravity (130 N) pulls into the incline and is balanced by normal force. The x-component of gravity acts to try to pull the block down along the incline.
Doesn’t the tension in the rope equal the weight of Block 2?
No. That would be true if Block 2 did not accelerate, but that is not the case here. You need to solve Newton’s 2nd Law given the forces and acceleration. (For example, if Block 2 accelerates downward, tension is only partially supporting it against gravity and so is less than mg.
Forces in the x-direction are tension and friction in the positive direction and the sin component of gravity in the negative direction.
Forces in the y-direction are normal force in the positive direction and the cos component of gravity in the negative direction.
The two blocks in this problem are connected together and so have the same value (magnitude) for acceleration. Therefore, I used the same symbol for the acceleration of each. For Block 1, this acceleration is up the incline, or in the +x direction. For Block 2, the acceleration is downward, or in the –y direction. “a” as the unknown quantity here is for the magnitude of the acceleration. I have used direction information in understanding that the objects move together, and therefore I must also put direction information into the equations as the sign of the a vector.
The force of gravity acts downward, which is the negative y-direction. Therefore, mg is given a negative sign in the equations. Do not also give 9.8 m/s2 a negative sign, or you will double count the direction.
In this case, the problem implies that the blocks are moving and so the frictional force present is that of kinetic (sliding) friction. Kinetic friction is an active force—its value is given by fr= µn regardless of the acceleration and other forces present.
If the assumption that the blocks is moving is incorrect, this will come out in the problem as an answer that doesn’t make sense. If that happens, you should revisit your assumptions about the magnitude and direction of friction.Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
Normal force on Block 1 is not the same as the gravitational force on Block 1 because the block is on an incline. Gravity pulls straight down—the y-component of gravity (130 N) pulls into the incline and is balanced by normal force. The x-component of gravity acts to try to pull the block down along the incline.
Why isn’t acceleration included on the free body diagram?
The free body diagram is a stylized drawing to help you visualize the cause of acceleration, and to directly map the drawing into the left hand side (ΣF) of Newton’s Second Law. Acceleration is the effect of the forces, and therefore is not included on the list of forces.
Why did you choose different coordinate systems for the two blocks?
The math is always easier if you pick one of your axes along the direction of acceleration. That way, acceleration only has one component and you have less linked equations. In this case, Block 2 accelerates downward and Block 1 accelerates along the incline, and so the y-axis for Block 2 was chosen downward and the x-axis for Block 1 was chosen along the incline. If you chose a horizontal/vertical coordinate system for Block 1, a1// would have both x- and y-components and you would end up having three linked equations in three unknowns instead of two.
Why didn’t you treat the two blocks as a single object?
You are asked to find the tension in the rope connecting the two blocks. If you treat them as a single system, you lose all information about forces that are internal to the system.
How do you work force problems with two objects (systems)?
You follow the same procedure as you do for a single system problem, but do it for each object. In other words, for this problem you will need to make two free body diagrams and set up two sets of equations. In addition, recognize that all forces of interaction between the two objects are Third Law pairs. Each object feels the magnitude of the interaction equally but in the opposite direction. So make sure to give the forces the same symbol on both free body diagrams to reduce the number of unknowns that you have to solve for in the final steps of the problem.
How did you know where to put the 25oangle?
There are two ways to approach this question. If you think visually, exaggerate the small and large angles on your drawing. In other words, 25o is less than half of a right angle, so draw the slope of the incline to be very small. Then you can see that mg makes a smaller angle with the –y axis than it does with the -x axis, and the smaller angle is 25o.
If you think geometrically, use the fact that the two small angles on a right triangle add up to 90o. The triangle on the first drawing made by the ground, the incline, and mg is a right triangle, so the angle between the incline (the -x axis) and mg must be (90-25)o=65o. It is equally fine to use the 65o angle, just note that sin and cos are reversed (because which side is opposite and which is adjacent depends on the triangle you draw.) You will get the same answer because sin(65o)=cos(25o).
I chose to use the first method simply because that is an easier way to determine the correct angle for most students.
My instructor taught us to rotate the FBD so that the y-axis is vertical. Why didn’t you do that?
Rotating the FBD picture is fine. It makes it easier for some people to visualize the x- and y-components of the gravitational force. Leaving the FBD oriented with the line of the incline is easier for other people to visualize how the forces relate to the motion of the block. Use whichever orientation is better for you!
What is an ideal pulley?
This is a pulley that is light enough and has low enough friction that you can neglect any effect it has on the tension in the rope. It changes the rope’s direction, but does not affect the magnitude of tension.
Why isn’t normal force included on the free body diagram of the hanging block?
Normal force is the contact force between two surfaces. It pushes out from the surfaces and keeps them from falling into each other. The hanging block is not resting on any surface.
No. That would be true if Block 2 did not accelerate, but that is not the case here. You need to solve Newton’s 2nd Law given the forces and acceleration. (For example, if Block 2 accelerates downward, tension is only partially supporting it against gravity and so is less than mg.
-
In this problem, we were asked to find the acceleration of two blocks tied together with a rope, and also to find the tension in the rope between them. The problem did not state for sure which direction the blocks are moving, or even if they are moving. Based on the relative masses of the blocks, we made the assumption that the hanging block accelerates downward and the sliding block upwards along the incline.
With that assumption, our solution is:
1.) The hanging block accelerates downward with a=5.5 m/s2 and the block on the incline accelerates upward along the incline, also with a=5.5 m/s2. This is just a little bit more than half the acceleration that the hanging block would have due to gravity alone, which makes sense. You would expect it to have a lower acceleration because of the upward tension in the rope due to the pull of the other block.
2.) The tension in the rope is 160 N. This value is about the same as the gravitational force on a 16 kg mass, again a number that makes sense. The 38 kg block is accelerating downward, and so the tension in the rope does not fully support it against gravity. Therefore, you know the tension in the rope must be less than (38 kg)g or less than 370 N.
Therefore, we correctly chose the direction of acceleration and friction.
- Why isn’t acceleration included on the free body diagram?
- Why did you choose different coordinate systems for the two blocks?
- Why didn’t you treat the two blocks as a single object?
- How do you work force problems with two objects (systems)?
- How did you know where to put the 25oangle?
- My instructor taught us to rotate the FBD so that the y-axis is vertical. Why didn’t you do that?
- What is an ideal pulley?
- Why isn’t normal force included on the free body diagram of the hanging block?
