While driving in the mountains, you notice that when the freeway goes steeply down hill, there are emergency exits every few miles. These emergency exits are straight dirt ramps which leave the freeway and are sloped uphill. They are designed to stop trucks and cars that lose their brakes on the downhill stretches of the freeway even if the road is covered in ice. You are curious, so you stop at the next emergency road. You estimate that the road rises at an angle of 100 from the horizontal and is about 100 yards (300 ft) long. What is the maximum speed of a truck that you are sure will be stopped by this road, even if the frictional force of the road surface is negligible?
This problem was used with permission of Dr. Ken Heller of the University of Minnesota Physics Education Research Group.
-
In this problem, you are asked to relate motion (the truck comes to a stop) to force (gravity). Force and motion of a single object are always related through Newton's Second Law, so this is a force or 2nd Law problem even though you are asked about velocity! You should always approach a problem first by thinking about the key interactions described, regardless of what quantity you are asked to find. Going from acceleration to velocity will be a second step in this problem.
Nowhere in this problem is the word "force" used. However, if you think about the problem you know that the truck comes to a stop as it moves up the slope because of gravity. The angle of the slope affects the stopping distance for any given speed, and so at the heart of the problem you are relating the cause of stopping (component of gravity) to the effect (stopping within a given distance.)
Newton's 2nd Law relates force and motion and describes that motion in terms of acceleration. In this problem, you are asked to describe motion in terms of velocity and distance. Therefore, once you find acceleration you will need to use a kinematic relationship to find the maximum initial speed of the truck. If you recognized the kinematics portion of the problem first, that is fine. You would quickly realize that you need to use Newton's Laws to understand acceleration.
The problem talks about velocity and distance. How do you know it is a force problem?
You may begin this as a kinematics (description of motion) problem and that is fine. If you do so, you will quickly see that you need to use Newton's 2nd Law to find the acceleration of the truck. However, in that case it is good to return to the problem when you have finished and understand that forces are the root of the question. The truck comes to a stop as it moves up a slope because of gravity. The angle of the slope affects the stopping distance for any given speed, and so at the heart of the problem you are relating the cause of stopping (component of gravity) to the effect (stopping within a given distance.)
-
Step 1
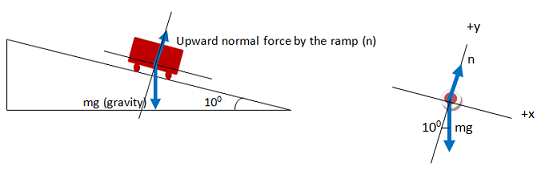
Your free body diagram is not yet complete because mg has both x- and y- components. Scroll down when you are ready to continue.
Why did you pick the x-axis to be along the incline?
The choice of coordinate system is yours. However, the math is always easier of you choose one axis to be in the direction of acceleration. In this case, the truck slows along the incline and so I chose the x-axis to be along the incline.
Why isn't friction included?
This problem explicitly tells you that friction in negligible--you want to know the fastest speed a truck could have and still stop in the worst road conditions. Therefore, you want to approximate friction as zero.
Why isn't there air resistance?
There is, indeed, air resistance on the truck. However, you are asked to estimate how fast you could go in a totally friction-free case, and so the implication is that you want to know how fast you can go with gravity only as the stopping force. Any air resistance present will reduce the stopping distance.
Why isn't buoyant force included on the free body diagram?
It is true that air puts a small buoyant force on the truck. However, the size of the upward buoyant force compared to the downward force of gravity is very small. (The ratio of the two is given by the ratio of the density of air to the density of the loaded truck.) So to the number of significant figures included in this problem, we do not need to take buoyant force into account.
Why isn't acceleration included on the free body diagram?
The free body diagram is a stylized drawing to help you visualize the causeof acceleration, and to directly map the drawing into the left hand side (ΣF) of Newton's Second Law. Acceleration is the effect due to the forces, and therefore is not included on the list of forces. It is certainly fine to include acceleration off to the side if you like.
Why isn't the length of the ramp included on the free body diagram?
Descriptive variables like displacement and velocity are useful for picturing motion. The description of motion is quantized through the kinematic relationships. Displacement and velocity will be useful on the picture for the kinematics part of the problem but do not help you to picture the forces on the truck. You can certainly label them on the initial picture if you wish, but do not include them on the FBD.
Why isn't velocity included on the free body diagram?
Descriptive variables like displacement and velocity are useful for picturing motion. The description of motion is quantized through the kinematic relationships. Displacement and velocity will be useful on the picture for the kinematics part of the problem but do not help you to picture the forces on the truck. You can certainly label them on the initial picture if you wish, but do not include them on the FBD.
Why isn't acceleration shown on the diagram?
The free body diagram is a sketch of the forces on an object, or the causes of motion. Acceleration is the effect of those forces and therefore does not show up on the FBD. It will make an appearance in the equation, and you can certainly draw it to the side if you wish.
This problem explicitly tells you that friction in negligible--you want to know the fastest speed a truck could have and still stop in the worst road conditions. Therefore, you want to approximate friction as zero.
It does not matter if you chose the incline to rise to the right or to the left. In either case, the 100 angle of the incline rises up from the horizontal.
There are two ways to know where to put the 100 angle on your FBD. If you think visually, exaggerate the small and large angles on your drawing. In other words, 100 is less than half of a right angle, so draw the slope of the incline to be very small. Then you can see that mg makes a smaller angle with the -y axis than it does with the +x axis, and the smaller angle is 100.
If you think geometrically, use the fact that the two small angles on a right triangle add up to 90 degrees. The triangle on the first drawing made by the ground, the incline, and mg is a right triangle, so the angle between the incline (the +x axis) and mg must be (90-10)0. It is equally fine to use the 800 angle that mg makes with the +x axis.
Normal force is present whenever two objects are in contact with each other. Its direction is out from the objects and perpendicular to the surfaces. In this case, the incline pushes against the truck at an angle straight out from the surface of the incline.
All objects near Earth experience a downward force of gravity equal to mass of the object x 9.8 m/s2 or 32 ft/ s2 in the English system. Do not worry that you don't know the mass of the truck. Focus on the phsyics of the problem now and you will see that mass divides out in the algebra.
----------------------------------------------------------------------------------------------
Step 2
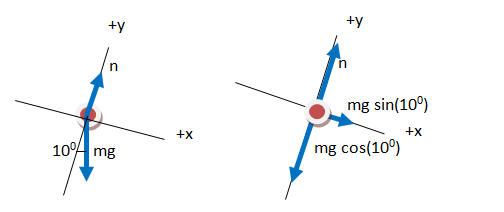
In the final FBD drawn here, all forces are divided into components. The contribution each force makes in the x-direction (along the incline) is shown explicitly, as is the contribution each force makes in the y-direction. The FBD is now a visual representation of ΣF=ma in each direction.
How did you divide the gravitational force into its components?
As you can see in the figure below, the x- and y-components of a vector make up the sides of a right triangle. The vector itself forms the hypotenuse (h). The side of the triangle opposite the angle that you use is given by h sinΘ and the side that touches the angle you use is given by h cosΘ (soh cah toa).
In this case, the x-component is opposite to the 100 angle and adjacent to the 100 angle, and so can be given by mg sin(100) as shown, or by mg cos(800) if you chose to use that angle instead. Likewise, the y-component is adjacent to the 100angle and is therefore given by mg cos(100).
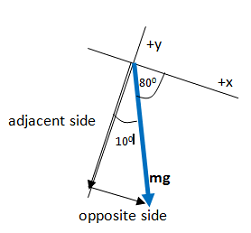
Doesn't the x-component always go with cosine and the y-component with sine?
No. Cosine goes with the component that is adjacent to Θ, and sine goes with the component that is opposite to Θ.
My instructor taught us to rotate the FBD so that the y-axis is vertical. Why didn't you do that?
Rotating the FBD picture is fine. It makes it easier for some people to visualize the x- and y-components of the gravitational force. Leaving the FBD oriented with the line of the incline is easier for other people to visualize how the forces relate to the motion of the truck. Use whichever orientation is better for you!
-
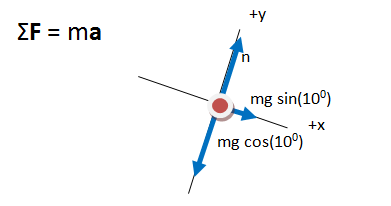
The key equation for any problem that relates forces and motion is Newton's Second Law. The left side of the equation takes into account the forces that act on the object, and the right side shows the effect of those forces. Regardless of what quantity you are asked to find, begin with the Second Law. If additional information is needed, it will become apparent as you proceed even when that additional information is the quantity you are asked to find.
I know this is a two part problem. What additional relation will I use?
Once you know acceleration from Newton's Law, you will be in position to relate velocity and displacement. (In other words, you want to know how fast the truck can move and still stop in a given distance.) The kinematic equation that relates velocity and displacement is
v22 = v12 + 2a(Δx).
If you already recognize that you will follow the force problem with a kinematics problem using acceleration to relate speed and distance, that is great!
-
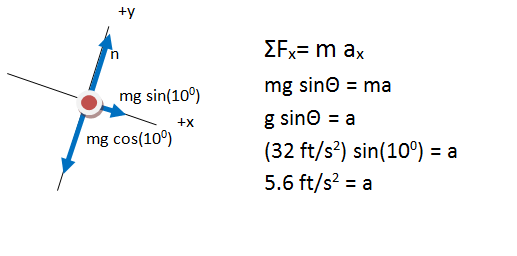
If there is no friction acting on the truck, it will slow with an acceleration of 5.6 ft/s2 because of the gravitational force. The problem asked you to find velocity. Scroll down to use this acceleration as you relate velocity and stopping distance.
Why is 32 ft/s2 positive? Why did you use 32 ft/s2 instead of 9.8 m/s2?
The force of gravity acts downward. For the coordinate system I chose, down has a component in the negative y-direction and a component in the positive x-direction. We always put the sign of the vector into the 2nd Law equation explicitly and then use the abosolute value of g to find magnitude. In this case, information in the problem was given in English units and so I used English units for g.
Why did you only work the problem in the x-direction?
In this case, the x-direction gave me the information that I needed. It is not wrong to also work the problem in y-direction. In that case, you would solve for the magnitude of the normal force.
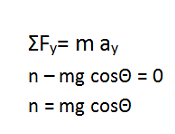
Why is acceleration positive? The truck is slowing down.
Remember, sign of acceleration indicates the direction of the acceleration and not whether it causes faster or slower (or turning) changes. If you have problems seeing the direction of acceleration, remember that it is in the same direction as the net force--in this case, down the ramp. If you drew your ramp sloping in the other direction, then your acceleration would, indeed, be in the negative x-direction.
In this case, you only need to work the problem in the x-direction to find the information that you need. It is not wrong to also work the problem in y-direction. In that case, you would solve for the magnitude of the normal force.
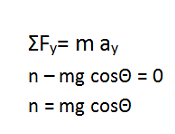
The only x-direction force in this problem is the sine component of gravity. If you drew your slope in the other direction, you would give that force a negative sign.
In this step, I dived both sides of the equation by mass. Because the acceleration of gravity is independent of mass, and because no other x-direction forces act on the truck, your answer is independent of the truck's mass. All trucks with the same initial speed will stop in the same distance.
Because English units were used for the information given in the problem, I used English units to find acceleration. If you used metric units instead, your answer would be 1.7 m/s2. Remember to use the absolute value of g in order to calculate the magnitude of the force--you already put in sign according to the direction.
Remember, sign of acceleration indicates the direction of the acceleration and not whether it causes faster or slower (or turning) changes. Acceleration in this problem is down the ramp, or in the positive direction. If you drew your ramp sloping in the other direction, then your acceleration would be in the negative x-direction.
In this case, the x-direction gives you all the information that you need to solve the problem. It is not wrong to also work the problem in y-direction. In that case, you would solve for the magnitude of the normal force.
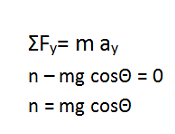
----------------------------------------------------------------------------------------------
Step 2
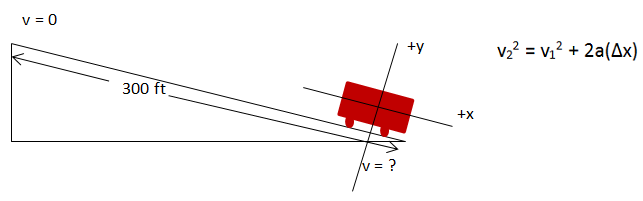
Now that you know the acceleration of the truck, you can use the kinematic (descriptive) equations to related velocity and stopping distance. As for the first step, I made the math easier by choosing one axis along the direction of the truck's acceleration. A useful picture for kinematic problems includes a picture of the motion and values of any descriptive variables that you know.
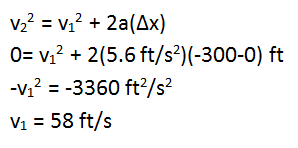
As long as the truck enters the ramp traveling less than 58 ft/s, it will be able to stop by the end of the ramp even without friction.
How did you know which kinematic equation to use?
There are three primary kinematic equations. One relates displacement and time, one relates velocity and time, and one relates displacement and velocity. As always, you should focus your thoughts not on "what does the problem ask for" but rather on the situation described. In this case, you are looking at the maximum velocity of the truck for a given stopping distance--you relate velocity and displacement.
Why is acceleration positive? The truck is slowing down.
Remember, sign of acceleration indicates the direction of the acceleration and not whether it causes faster or slower (or turning) changes. If you have problems seeing the direction of acceleration, remember that it is in the same direction as the net force--in this case, down the ramp. If you drew your ramp sloping in the other direction, then your acceleration would, indeed, be in the negative x-direction.
You are told that the truck continues along the ramp for a distance of 300 ft before coming to rest (v = 0). I chose the origin to be at the initial location of the truck (x = 0) which means that for my chosen coordinate system the final position was x = - 300 ft.
The truck's velocity along the ramp slows to a stop. Therefore, the truck's acceleration is along the ramp, and I chose the x-axis accordingly.
58 ft/s probably does not have much meaning for you. Make sure to go to the Understand page to evaluate your answer.
Make sure to keep track of subscripts and what they mean. The truck's final velocity, or v2 is 0. Its initial velocity (v1) is unknown.
Make sure to keep track of subscripts and what they mean. Δx means (final position - initial position.) As I have chosen my coordinate system, the initial position is 0 and the final position 300 m to the left, or in the negative direction.
There are three primary kinematic equations. One relates displacement and time, one relates velocity and time, and one relates displacement and velocity. As always, you should focus your thoughts not on "what does the problem ask for" but rather on the situation described. In this case, you are looking at the maximum velocity of the truck for a given stopping distance--you relate velocity and displacement.
0 - v12 = - v12
-
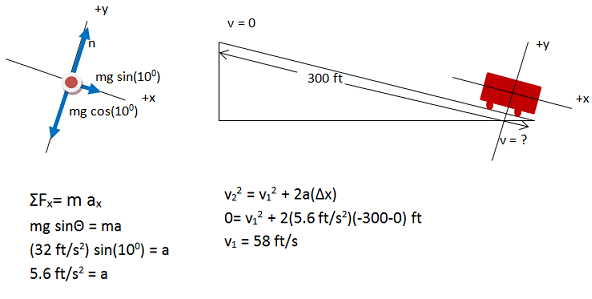
As long as a truck, or any vehicle, travels less than 58 ft/s or 39 mph, it can stop without friction on the upward incline. Although you may not have the experience or intuition to know if this speed makes sense given the length and slope of the incline, you can recognize that it is a reasonable design speed for the situation.
If you did not initially recognize that this is a two part problem (in which you solve Newton's 2nd Law for acceleration and then use that acceleration to describe the motion), make sure to look at the overall solution now to see how the two parts fit together.
Because your solution is independent of mass, it is not limited to only heavy vehicles like trucks.
(58 ft/s)(1 mi/5280 ft)(3600 s/hr) = 39 mi/hr
As you can see in the figure below, the x- and y-components of a vector make up the sides of a right triangle. The vector itself forms the hypotenuse (h). The side of the triangle opposite the angle that you use is given by h sinΘ and the side that touches the angle you use is given by h cosΘ (soh cah toa).
In this case, the x-component is opposite to the 100 angle and adjacent to the 100 angle, and so can be given by mg sin(100) as shown, or by mg cos(800) if you chose to use that angle instead. Likewise, the y-component is adjacent to the 100angle and is therefore given by mg cos(100).

Don't I need to know the mass of the truck?
You should always focus your solution by thinking about the physics of the problem, rather than by what is given or not given. In some cases (such as this one), information that you think you will need cancels out. In other cases, you will be able to look up the information or calculate it from other information in the problem. In any case, begin with a focus on the physics and not on the given or requested quantities.
This problem mixes kinematics and dynamics. Where do I start?
It doesn't matter. On two part problems, you can begin with either part of the problem--whichever is more clear to you. Depending on what you do first, you may need to pause in your solution to work the second part of the problem, and that is ok. For example, if you begin with the description of motion on this problem, you will see that you need to know acceleration. So you can pause in your work, use force to find acceleration, then return to the description of motion knowing the value that you needed. That said, make sure to look at the Identify page to understand that it is conceptually nicer to start with force.
