You are towing a trailer of large rocks up a steep road that is inclined 120 to the horizontal. Although you are careful to drive at a steady speed of 15 m/s, when you get 2400 m along the road one of the rocks slides off the back of the trailer and rolls down the incline. How fast is the rock going when it reaches the bottom? If you find instead that the speed of the rock is 40 m/s at the bottom, what is the average drag force on the rock? Assume that the trailer is low enough to the ground that the rock does not lose any energy as it hits the ground.
-
In this problem, you are asked to find the speed of a rock when you are given its initial speed and position. If non-conservative forces are either known or small and if energy is converted from one form to another between the locations, then any time you relate speed and position of an object at two different points, conservation of energy is the most direct way to understand the problem. It is especially true in this case where some of the energy is converted into rotational motion as well as translational motion.
In this case, you start out with translational kinetic energy and stored energy due to the height of the rock and convert them into translational and rotational kinetic energies.
You are told in the statement of the problem to ignore any energy losses as the rock slides off the trailer. You are also told that the rock rolls along the ground. If an object rolls without slipping, friction does not take any energy out of the system. The first part of the problem implies that the rock rolls with no energy loss. In the second part of the problem, you are asked to find drag force with a known final energy. Therefore, you have the information that you need in order to work this as a conservation of energy problem.
Can this problem be worked using kinematics?
Although it is certainly true that you are asked to describe motion in this problem, it is always easier to use energy when you can. The rotational motion of the rock complicates this problem further, making it very difficult to work with kinematics.
-
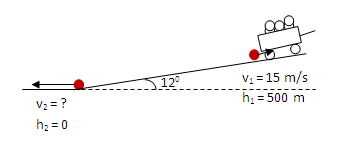
Because energy problems relate motion and position, a useful picture is a picture of the motion with positions and velocities labeled. Energy is a scalar quantity and so you do not need to divide vectors into components.
How did you pick h = 0?
It is only the difference in height that has physical significance. Therefore, you can pick h = 0 at any point. I chose the lowest point in the motion. If you instead chose the starting point, just make sure that you use a negative height for h2.
How do you know h1 = 500 m? Why isn't it 2400 m?
Gravitational energy depends on the height of the object, and not on how the object reached that height. Because I am given the distance along the incline (the hypotenuse) and the angle of the incline, I can calculate height using sine as shown:
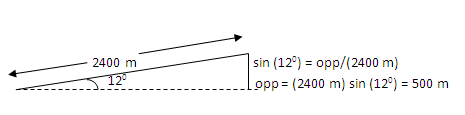
How did you know which way to draw the incline?
It doesn't matter. As long as you show a slope of 120 above the horizontal, your hill can rise in either direction.
Gravitational energy depends on the height of the object, and not on how the object reached that height. Because I am given the distance along the incline (the hypotenuse) and the angle of the incline, I can calculate height using sine as shown:

It is only the difference in height that has physical significance. Therefore, you can pick h = 0 at any point. I chose to make h2 = 0 and h1 positive. If you instead chose h1 = 0, just make sure that you use a negative 500 m for h2.
Because the rock is initially moving with the trailer and does not lose energy as it slides to the ground, it has an initial speed of 15 m/s.
The rock originally moves uphill with the truck. It will roll due to static friction and slow and reverse direction due to gravity.
-
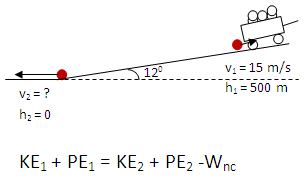
Any time you understand the motion of an object by looking at its energy, you begin with the Conservation of Energy equation.
This is not how my book writes the Conservation of Energy equation. What is Wnc?
Wnc is any work done by non-conservative forces, such as friction or a push, which take energy in or out of the system of interest. Some books teach you to always think about this term, others only add it if it isn't zero. Still others may write it as KE1 + PE1 + Eadded to the system = KE2 + PE2 + Eleaving the system. If there is no significant non-conservative force (as is the case in the first question) then all three versions of the equation are equivalent. Including Wnc in some form is more general and gives an equation that is true in all situations, including those with non-conservative forces. In the second part of the problem when you are asked about drag, you must use this version.
Wnc is any work done by non-conservative forces, such as friction or a push, which take energy in or out of the system of interest.
Some books use K instead of KE for kinetic energy. Note that this is total kinetic energy. In this problem, there will be both translational and rotational terms.
Some books use U instead of PE for potential energy. In this problem, the only potential energy is gravitational potential energy.
-
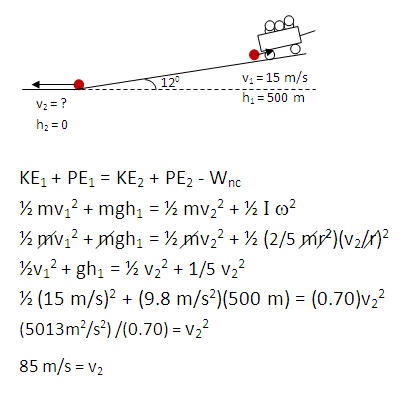
If the rock rolls without slipping, it will have a translational speed of 85 m/s at the bottom of the incline. Scroll down to find how much drag force is required if the block is to only have a speed of 40 m/s at the bottom of the hill.
How did you know to include rotational kinetic energy?
It takes energy to rotate about an axis (to spin) just as it takes energy to move translationally. Because the entire rock is rolling, I know that I can't ignore the rotational kinetic energy as I can, for example, in the case of tires on a car. (In that case, the mass of the tires is very small compared to the mass of the whole car.)
What happened to mass?
Because mass is present in every term, I divided it out in the 3rd line.
Friction only takes energy out of system if an object slides along a surface. If the rock rolls and does not slip, only static friction acts and there is no non-conservative work done on the rock.
When the rock initially slides off the trailer, it is moving with the speed of the trailer and so there is an initial kinetic energy. However, it is not yet rolling and so there is not also a rotational energy term. It will begin to roll due to the friction with the ground.
Because I chose h = 0 at the bottom of the hill, the rock has an initial gravitational potential energy. There are no other forms of potential energy (such as spring or electric) that need to be considered in this problem.
At the bottom of the incline, the rock is not only moving translationally but it is also rotating. Therefore, KE2 includes both translational and rotational terms.
The values for Point 1 can be put into the equation directly from your picture.
The values for Point 2 can be put into the equation directly from your picture.
Height was chosen to be zero at the bottom of the hill, so there is no potential energy there. If you included a mgh term, that is fine. You will just set it to 0 in the next step.
The moment of inertia of an object depends on the mass of the object and on how that mass is distributed. In this case, I assumed that the rock is spherical, and looked up the moment of inertia for a solid sphere. Make sure you don't use moment of inertia of a shell, which means a hollow object. If you assumed a different solid shape, such as a cylinder, that is fine as long as you work the problem in the same way.
Angular velocity is defined as linear velocity divided by radius: ω = v/r
The sign of gravitational potential energy comes from the sign of h. Therefore, make sure to use a positive value for g.
1/2 + 1/5 = 0.50 + 0.20 = 0.70
In this step, I squared ω and divided out the r2s.
----------------------------------------------------------------------------------------------
Step 2
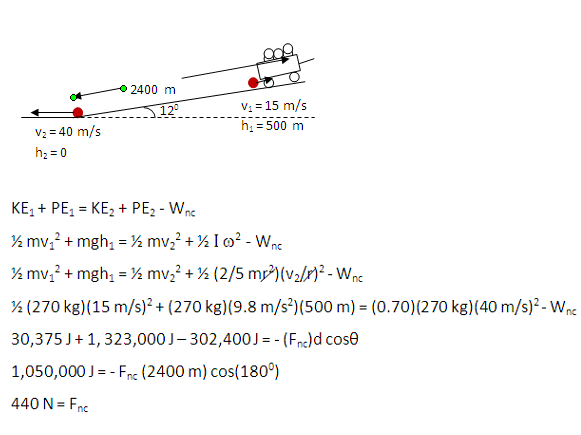
A non-conservative force of 440 N acting against the rock is required if it is to only reach a speed of 40 m/s at the bottom of the hill.
Why didn't you divide out m?
In this case, m was not present in all terms. The Wnc term does not directly contain mass and so it cannot be divided out. In order to cancel a variable, it must be present in every term in an equation.
A non-conservative force is any force that takes energy in or out of the system. In this part of the problem, you are asked to calculate how much drag is required to take energy out of the system. Wnc is not 0.
In the second question, the rock has a speed of 40 m/s at the bottom of the hill.
Because the r2s divide out in the rotational kinetic energy terms, I factored mv2 out of both terms, leaving 1/2 and 1/5. As for part 1, 1/2 + 1/5 = 0.70.
The work done by any force F is equal to that force times the distance over which it acts, times the sine of the angle between the force and the direction of motion. W = Fdcosθ.
Drag acts against the motion of an object. In other words, θ is 180 degrees. Cos(1800) = -1. Therefore, -Wnc is overall positive. This makes sense: if energy leaves the system, that amount of energy must be added to the final energy of the system in order to account for all of the initial energy.
The distance over which a non-consevative force acts is measured along the path of the motion. You want to use the path of the rock and not just the height.
-
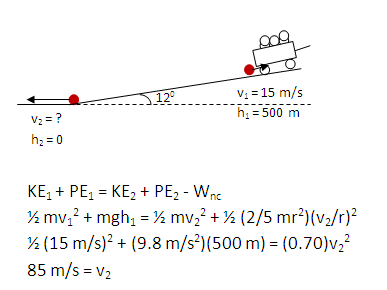
If no drag force is present, the initial kinetic and gravitational energies of the rock remain in the system and are converted into translational and rotational kinetic energies. The energy chain for this process is
translational kinetic energy + gravitational potential energy --> translational and rotational kinetic energy
If drag force is present, as in the second question, then some of the initial energy leaves the system and the energy chain is
translational kinetic energy + gravitational potential energy --> translational and rotational kinetic energy + thermal energy
This results in a slower velocity of the rock at the bottom of the hill.
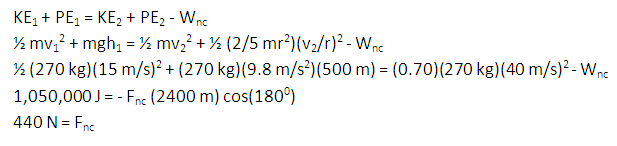
It takes about 700 N or so to lift an adult human, and so this is a reasonable answer for the necessary force.
How did you pick h = 0?
It is only the difference in height that has physical significance. Therefore, you can pick h = 0 at any point. I chose the lowest point in the motion. If you instead chose the starting point, just make sure that you use a negative height for h2.
How big is the rock? What shape is it?
Always begin the problem by thinking about the key physics involved. Once you set up the physics, you can find or estimate any additional information that you might need. In this case, it will turn out that mass and radius of the rock are not needed but I will need to assume a shape for the rock.
Do I need to think about friction in this problem?
If there was no friction present, the rock would slide down the incline. Because it is rolling, you know that static friction acts on the rock. However, as long as the rock rolls without slipping there is no sliding motion and so friction does not take energy out of the system. The implication in the first part of the problem is that there is no slipping. In the second question, you are asked to compare this ideal case with a measurement involving sliding friction or other sources of drag.
Does the rock start from rest at the top of the incline?
No. The rock is originally moving with the truck. You are told that any energy loss as the rock slides off the truck are small enough to ignore.
Does it matter that the rock might originally roll up the incline?
No--the rock will slow to a stop as it rolls uphill, then increase in speed as it rolls back down. Because no energy leaves the system, you know its original translational kinetic energy is still in the system.
What do you mean by "translational" kinetic energy?
This is the energy due to the motion of the center of mass of an object: 1/2 mv2.
