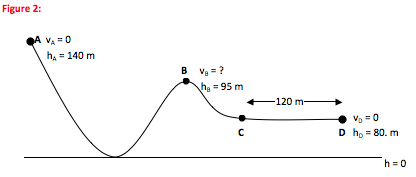
An 850 kg roller-coaster is released from rest at Point A of the track shown in the figure. Assume there is no friction or air resistance between Points A and C. How fast is the roller-coaster moving at Point B? What average force is required to bring the roller-coaster to a stop at Point D if the brakes are applied at Point C?
-
In this problem, you are first asked to find a speed of a roller-coaster when you are given information about how its height changes.
If non-conservative forces are either known or small and if energy is converted from one form to another between the locations, then any time you relate speed and position of an object at two different points conservation of energy is the most direct way to understand the problem.
In this case, you start out with stored gravitational potential energy and convert part of that energy to kinetic energy.
In the second part of this problem, you are asked to find stopping force given stopping distance. In other words, you want to find how much force is required to convert the roller-coaster’s kinetic energy into heat and sound in a given distance. Again, energy is the most direct way to understand this problem.
-
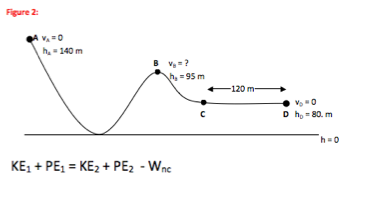
Any time you understand the motion of an object by looking at its energy, you begin with the Conservation of Energy equation. This form of the equation works equally well for the first part of the problem (where Wnc = 0) and for the second question (where you need to solve for Wnc.)
-
Step 1
At Point B, part of the gravitational potential energy of the roller-coaster has been converted to kinetic energy, and the roller-coaster has a speed of 30 m/s. Continue to Step 2 to solve for the stopping force required to bring the roller coaster to rest at Point D.
Step 2
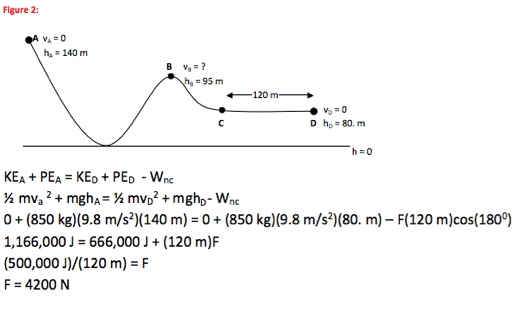
An average force of 4200 N is required to stop the roller-coaster by Point D when the brakes are applied at Point C. No further mathematical solution is required for this problem.
Can this problem be worked using kinematics and dynamics?
Yes, but why would you want to? The Conservation of Energy equation between Point A and Point B reduces to the kinematic equation v2 = v02 + 2a(Δx), although it takes some effort to prove that correctly given that velocity and displacement are vectors. You can solve for the motion between Point C and D through a combination of kinematics and dynamics. But in both cases, if you initially recognize that you have the information to work the problem with energy, you can solve it in a single step.
How do you pick h = 0?
All that matters for describing motion and energy is that you explicitly state where your reference point is. In this case, all heights are given referenced to the ground, and so I chose the ground to be h = 0. It is equally fine to pick the lowest point considered in the problem (Point D) to be h = 0. In that case,
hA = 60. m and hB = 15 m.
Why don’t you need to label information about Point C?
Because there is no friction between Points A and C, the energy of the rollercoaster remains constant over that portion of the motion. Therefore, there is no need to solve for the speed of the rollercoaster at Point C. You can set up the Conservation of Energy equation between Point A and Point D. However, it is perfectly fine to solve the intermediate step of finding the velocity at Point C if you like.
This is not the way my book writes the Conservation of Energy equation. What is “Wnc”?
Wnc is any work done by non-conservative forces, such as friction or a push, which take energy in or out of the system of interest. Some books teach you to always think about this term, others only add it if it isn’t zero. Still others may write it as KE1 + PE1 + Eadded to the system = KE2 + PE2 + Eleaving the system. If there is no significant non-conservative force (as is the case in the first question) then all three versions of the equation are equivalent. Including Wnc in some form is more general and gives an equation that is true in all situations, including those with non-conservative forces such as the second question in this problem.
Why is 9.8 m/s2 positive?
Gravitational potential energy can be either negative or positive, depending on whether the object is below or above the h = 0 point. In other words, the sign for PEg comes from the sign of h. + 9.8 m/s2 is always put in for g.
How did you know which points to compare?
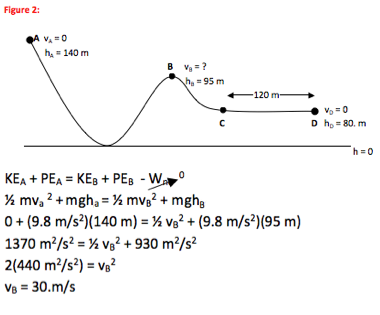
We are given complete information about the energy of the roller-coaster at Point A and are asked about its motion at Point B. Therefore, the first question can be answered by comparing Points A and B.
What happened to mass?
Mass is present in all terms of the equation, and so it can be divided out. It is equally correct to include it.
Why is 9.8 m/s2 positive?
Gravitational potential energy can be either negative or positive, depending on whether the object is below or above the h = 0 point. In other words, the sign for PEg comes from the sign of h. + 9.8 m/s2 is always put in for g.
How did you know which points to compare?
We are given complete information about the energy of the roller-coaster at Point A and are asked about the force required to stop it by Point D. Therefore, the second question can be answered by comparing A and D. Because the energy in the roller-coaster is the same from A to C, it is equally fine to compare B to D or C to D (if you solve for vC first.)
Why did you need to include mass?
Mass cannot be divided out of this equation because it does not appear in all terms. This makes physical sense—the force required to stop the roller-coaster depends on its mass.
At the start of the problem, the roller-coaster is at the top of the hill at Point A. Because it is released from rest, its starting velocity is zero. The force of gravity will cause it to speed up as it moves down the hill.
Because there is no friction between Points A and C, the energy of the rollercoaster remains constant over that portion of the motion. Therefore, there is no need to solve for the speed of the rollercoaster at Point C. You can set up the Conservation of Energy equation between Point A and Point D. However, it is perfectly fine to solve the intermediate step of finding the velocity at Point C if you like.
Some books use PE for potential energy. Others use P.E. and others use U. All are equivalent and refer to the same thing.
Wnc is any work done by non-conservative forces, such as friction or a push, which take energy in or out of the system of interest. Some books teach you to always think about this term, others only add it if it isn’t zero. Still others may write it as KE1 + PE1 + Eadded to the system = KE2 + PE2 + Eleaving the system. If there is no significant non-conservative force (as is the case in the first question) then all three versions of the equation are equivalent. Including Wnc in some form is more general and gives an equation that is true in all situations, including those with non-conservative forces such as the second question in this problem.
There are no significant non-conservative forces (like friction) present between Points A and B, and so the work done by non-conservative forces is about zero.
There are no springs or other conservative forces beyond gravity present, so the only potential energy term at both locations is gravitational potential energy.
We are given complete information about the energy of the roller-coaster at Point A and are asked about its motion at Point B. Therefore, the first question can be answered by comparing Points A and B.
Mass is present in all terms of the equation, and so it can be divided out. It is equally correct to include it.
Gravitational potential energy can be either negative or positive, depending on whether the object is below or above the h = 0 point. In other words, the sign for PEg comes from the sign of h. + 9.8 m/s2 is always put in for g.
The values for Point A can be put into the equation directly from your picture.
The values for Point can be put into the equation directly from your picture.
The values for Point D can be put into the equation directly from your picture.
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
There are no springs or other conservative forces beyond gravity present, so the only potential energy term at both locations is gravitational potential energy.
We are given complete information about the energy of the roller-coaster at Point A and are asked about the force required to stop it by Point D. Therefore, the second question can be answered by comparing A and D. Because the energy in the roller-coaster is the same from A to C, it is equally fine to compare B to D or C to D (if you solve for vC first.)
Mass cannot be divided out of this equation because it does not appear in all terms. This makes physical sense—the force required to stop the roller-coaster depends on its mass.
Gravitational potential energy can be either negative or positive, depending on whether the object is below or above the h = 0 point. In other words, the sign for PEg comes from the sign of h. + 9.8 m/s2 is always put in for g.
WF = Fd cosθ. In this case, the non-conservative force acts between Points C and D, or over a displacement of 120 m as shown in the figure.
WF = Fd cosθ. In this case, the non-conservative force is the stopping force. Displacement (d) is to the right in this drawing and stopping force is to the left, so the angle between them is 1800.
– F(120 m)cos(1800) = - F(120 m)(-1) = +F(120m) This makes physical sense—stopping force takes energy out of the system and so Ein the system at the start = Ein the system at the end + E that left the system
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
How do you pick h = 0?
All that matters for describing motion and energy is that you explicitly state where your reference point is. In this case, all heights are given referenced to the ground, and so I chose the ground to be h = 0. It is equally fine to pick the lowest point considered in the problem (Point D) to be h = 0. In that case,
hA = 60. m and hB = 15 m.
Can this problem be worked using kinematics and dynamics?
Yes, but why would you want to? The Conservation of Energy equation between Point A and Point B reduces to the kinematic equation v2 = v02 + 2a(Δx), although it takes some effort to prove that correctly given that velocity and displacement are vectors. You can solve for the motion between Point C and D through a combination of kinematics and dynamics. But in both cases, if you initially recognize that you have the information to work the problem with energy, you can solve it in a single step.
Don’t I need to know the coefficient of friction to solve for stopping force?
No. Because you are given information about the motion of the roller-coaster, you can solve for force using energy (or Newton’s Second Law) rather than plugging into the definition of friction.
Don’t I need to know the angles the hills make with the horizontal?
No. Because there is no friction over this portion of the track, the only energy conversion that takes place is between kinetic energy and gravitational potential energy. PEg depends on height, but not on distance covered along the track.
-
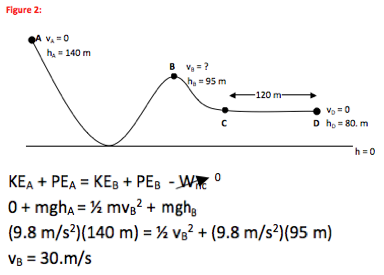
In this problem, you are first asked to find how fast a roller-coaster moves at a given point on the track. The energy conversion chain for this motion is
gravitational potential energy→kinetic energy + gravitational potential energy
Because essentially no energy is lost from the system (you are told friction and air resistance are negligible,) the amount of energy in the system remains constant throughout. This means energy can be compared at any two points. In this case, we are given information about the energy at A and are asked for information B. In other words,
gravitational potential energyA = kinetic energyB + gravitational potential energyB or mghA= ½ mvB2 + mghB as seen in the equation above.
The value of 30 m/s is reasonable for motion of a roller-coaster.
KEA + PEA = KED + PED - Wnc
0 + mghA = 0 + mghD - Wnc
(850 kg)(9.8 m/s2)(140 m) = (850 kg)(9.8 m/s2)(80. m) – F(120 m)cos(1800)
F = 4200 N
In the second part of the problem, you are asked to find the force required to stop the roller-coaster between Points C and D. The energy chain for this motion is
gravitational potential energy→gravitational potential energy + heat and sound or mghA = mghB –Fd cos(1800) as seen in the equation above.
The value of 4200 N is about half the weight of the roller-coaster, so would require a coefficient of friction of about 0.5. Again, a reasonable value.
There are many description of motion problems which can be solved by either kinematics or energy. Energy is almost always the most efficient way to approach these problems as long as enough information is given. (Energy does not require dividing vectors into components, or doing Second Law problems to find acceleration.) In this case, the changing position of the roller-coaster reflected a change in the energy of the system, we are not asked to find time, and there are no significant unknown energy losses from the system. Therefore, we are able to approach this question by tracking the energy.