You pour 320 g (0.32 kg) of boiling tea into an insulated travel mug. How many 12 g (0.012 kg) cubes of ice do you need to add in order to cool the tea to a temperature of no more than 57 oC? Hints: Tea is essentially water and so you can use any constants that you look up for water to apply to tea as well. Don’t worry about any changes to temperature of the travel mug.
-
In this problem, you are first asked about a situation in which the temperature of one substance (tea) changes because of its interaction with another substance (ice). Temperature is a measure of thermal energy, so in other words thermal energy goes from the tea to the ice. This is a Conservation of Energy problem. Because only thermal energies are involved, you do not need to look at mechanical (kinetic, potential) energies.
-
Unlike mechanical energy problems, no figure is needed in this case. All energy changes are from thermal energy going from the tea to the ice. A picture will not add to understanding or organization of this problem.
-
The energy chain for this problem is
Thermal energy of tea → thermal energy of ice or
-ΔQtea = ΔQice
-mteacteaΔTtea = miceLof melting + micecmelted iceΔTice
Any time you understand the motion of an object by looking at its energy, you begin with a statement of Conservation of Energy. You don’t need to track kinetic and potential energies here so it is easiest to begin with an energy chain.
-
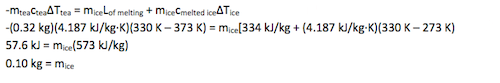
In order for the tea to cool from boiling to 57oC, it must lose 57.6 kJ of thermal energy. This is enough to melt and warm 0.10 kg of ice. (0.10 kg)/(0.012 kg/cube) = 8.3 ice cubes so you must add nine ice cubes to bring the temperature of the tea below 57o degrees.
My text book has separate chapters for thermodynamics and mechanical energy. Why did you call this an energy problem?
The same core physics (energy is never created or destroyed but can change in form) is behind all energy problems, regardless of how the energy changes. Physicists studying motion tend to look at problems in which the key conversions are between kinetic, potential and thermal energies; thermal physicists tend to look at situations in which the key conversions are within thermal energy itself. In all cases, you begin with a statement of conservation of energy, plug in the energy changes for your specific situation, and proceed in the same way.
Can this problem be worked using kinematics or dynamics?
No. All energy changes are to internal energies and not from changes to location or velocity.
You don’t give any information in this problem. How do I begin?
Begin by thinking about what is happening in the problem. Ice cools the tea because thermal energy leaves the tea and melts and warms the ice. So this is an energy problem. Once you set up the correct equation, you can go to the web or your text book to look up any physical constants that you need.
You don’t give any information in this problem. How do I begin?
Begin by thinking about what is happening in the problem. Ice cools the tea because thermal energy leaves the tea and melts and warms the ice. So this is an energy problem. Once you set up the correct equation, you can go to the web or your text book to look up any physical constants that you need.
Why did you convert temperatures to Kelvin?
Remember that ΔT = Tfinal – Tinitial. The tea begins at boiling or 100 oC and the ice begins at 0 oC. Both end up (Tfinal) at 57 oC. If you recognize that the degree size in Celsius is the same as the degree size in Kelvin, you don’t need to convert and can just use (57 – 100) = - 43 K for the tea and (57 – 0) = 57 K for the ice.
ΔQ = change in thermal energy = mcΔT
Mechanical energy problems are those that involve a change in velocity as an object changes its position.
Energy leaves the tea, so its change is negative.
Part of the energy that leaves the tea goes to a state change in melting the ice (mL) and the remaining energy from the tea warms
the melted ice from 0 oC to 57 oC (mcΔT).It is fine to begin with Conservation of Energy as
KE1 + PE1 = KE2 + PE2 – Wnc
You then recognize that KE1 = KE2 and PE1 = PE2, leaving –Wnc = 0. You then need to look deeper into the changes within Wnc, taking you to the equation -ΔQtea = ΔQice .You can find the specific heat of water in your text book or on line. It is fine to use kJ and kg as I did here, or to use J and kg or calories and grams. Just be consistent in your units throughout the problem. You were told in the statement of the problem to use the same value for tea and for water.
Latent heats for different substances can be found in your text book or on line. Make sure to use the latent heat of melting and not of vaporization—it takes more energy to vaporize a kg of water than to melt a kg of ice.
Remember that ΔT = Tfinal – Tinitial. The tea begins at boiling or 100 oC and the ice begins at 0 oC. Both end up (Tfinal) at 57 oC. If you recognize that the degree size in Celsius is the same as the degree size in Kelvin, you don’t need to convert and can just use (57 – 100) = - 43 K for the tea and (57 – 0) = 57 K for the ice.
It takes 573 kJ to bring one kg of ice to 57 oC. 334 kJ of energy are required to melt the ice, and the remaining 239 kJ are required to warm the melted water.
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
You don’t give any information in the problem. How do I begin?
Begin by thinking about what is happening in the problem. Ice cools the tea because thermal energy leaves the tea and melts and warms the ice. So this is an energy problem. Once you set up the correct equation, you can go to the web or your text book to look up any physical constants that you need.
My text book has separate chapters for thermodynamics and mechanical energy. Why did you call this an energy problem?
The same core physics (energy is never created or destroyed but can change in form) is behind all energy problems, regardless of how the energy changes. Physicists studying motion tend to look at problems in which the key conversions are between kinetic, potential and thermal energies; thermal physicists tend to look at situations in which the key conversions are within thermal energy itself. In all cases, you begin with a statement of conservation of energy, plug in the energy changes for your specific situation, and proceed in the same way.
Can this problem be worked using kinematics or dynamics?
No. All energy changes are to internal energies and not from changes to location or velocity.
-
The energy chain for this problem is
Thermal energy of tea → thermal energy in ice
There are no changes in mechanical energy and so no need to track those terms. In equation form,
-ΔQtea = ΔQice
-mteacteaΔTtea = miceLof melting + micecmelted iceΔTice
The first term in this equation represents the amount of energy the tea lost as it cooled, the second term is the amount of energy absorbed by the ice as it melted, and the final term is the amount of energy absorbed by the melted water as it warmed to 570C. Mathematically, the solution
-(0.32 kg)(4.187 kJ/kg∙K)(330 K – 373 K) = mice[334 kJ/kg + (4.187 kJ/kg∙K)(330 K – 273 K)
57.6 kJ = mice(573 kJ/kg)
0.10 kg = mice or 8.3 ice cubes
is physically reasonable.
