According to the website www.zeroto60times.com, a 2010 Ford Mustang GT can acceleration from zero to 60 mph ( 26.8 m/s) in 4.9 s. What is the average acceleration of the car during that period of time? If acceleration on the car is constant, how far does the car travel in those 4.9 s?
-
In this problem, you are asked to describe the motion (acceleration, location) of the car. Whenever you are asked to describe the motion of an object without worrying about the cause of that motion, you have a kinematics problem.
-
There are three key kinematic equations. If you carefully select the equation which most directly describes the situation in your problem, you will not only solve the problem in fewer steps but also understand it better. The three equations, written for motion in the x-direction, are:
1. x = x0 + v0Δt + ½ a(Δt)2 (relates position and time)
2. v = v0 + aΔt (relates velocity and time)
3. v2 = v02 + 2a(Δx) (relates velocity and position)
a) The acceleration of the car is a variable in all three equations, so this question drives home the point that you can’t pick your equation just by what is requested in the problem. In this case, you want to find the acceleration that is needed for the car to reach a velocity of 26.8 m/s in a time interval of 4.9 s. The question relates velocity and time, so you want to use equation 2.
b) You are asked how far (position) the car travels in 4.9 s (time), so you want to use equation 1.
-
Step 1:
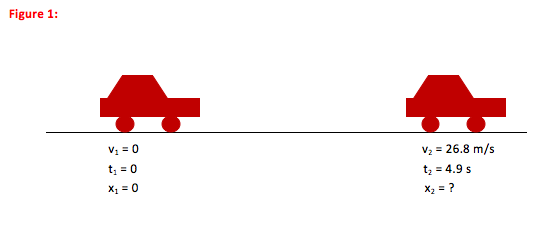

The average acceleration of the car as it moves from Point 1 to Point 2 is the information that was requested in the first of the problem. Scroll down to step 2 to answer the second question.
--------------------------------------------------------------------------------------------
Step 2:

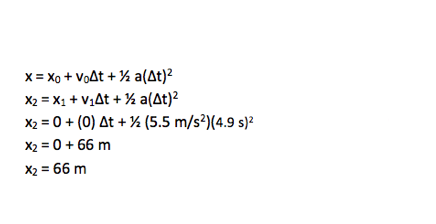
The second part of the problem asked for the distance the car traveled in the 4.9 s. No further mathematical solution is required.
The first point described in the problem is when the car is at rest, or has a velocity of zero. I am free to choose t = 0 and x = 0 whenever and wherever I like, because only the time and distance intervals have physical significance. I chose both time and position to be zero at the starting point of the problem.
The second point described in the problem occurs 4.9 s after the starting point. The car has traveled an unknown distance and reached a speed of 26.8 m/s.
Equation 2 is simply the definition of average acceleration (a = Δv/Δt) rewritten. If you recognized that you just have a definition problem in the first question, you saved yourself one step of algebra!
By convention, we choose x0, v0, and t0 to be the earlier (in time) of the two points considered in the equation. With that convention, Δt is positive. Therefore, in this problem, “v” refers to Point 2 and “v0” refers to Point 1.
The t in the kinematic equations refers to the time interval between the two points in the equation, with x0 occurring at the earlier time. I use Δt rather than t to be explicit that this is a time interval (t – t0) and not a point in time.
Some text books will give more than three kinematic equations—for example, they may provide “range equations” or different versions of the equations for horizontal and vertical motion. Those are just these three equations solved for special cases. In my view, it is better to know and understand three equations that will always work than to memorize many equations which are specific to certain situations only.Remember, multiplying by 0 gives 0.
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution. The answer in this problem is quite sensitive to the stage at which you rounded numbers, so as long as you followed the same procedure don’t worry if your number is a little bit different.
By convention, we choose x0, v0, and t0 to be the earlier (in time) of the two points considered in the equation. With that convention, Δt is positive. Therefore, in this problem, “x” refers to Point 2 and “x0” refers to Point 1.
Remember, multiplying by 0 gives 0.
The acceleration of the car in this case is 5.5 m/s2. It is true that gravity acts on the car, but it is balanced by the upward force from the road. So the car does not experience an acceleration in the vertical direction. In the kinematic equations, acceleration refers to the actual motion of the object and not to effects that any given force would have if it acted alone.
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
(60 miles/hour)(1.609 km/mile) = 96.54 km/hour
(96.54 km/hour)(1000 m/km) = 96,540 m/hour
(96,540 m/hour)(1 hour/3600 s) = 26.8 m/s?
Note that in general, the conversion between mph and m/s is (1.609 km/mile)(1000 m/km)(1 hour/3600 s) = 0.447 m/mile hr/s and so you can save steps by just multiplying speed in mph by 0.447 to get speed in m/s.How do you pick x = 0 and t = 0?
How do you know x1 and t1 are 0?
All that matters for describing motion is that you explicitly state where your reference points are. In this case, I chose to start the clock and measure distance from the starting point in the problem. No matter what I call x1 and t1, the intervals between them and x2 and t2 will be the same.
My book uses variables like x, x0, v, v0, and t. Why do you use 1 and 2 as subscripts, and Δt instead of t?
The kinematic equations relate position and velocity at any two points in the motion. Because many problems provide or ask about information at more than two points, I identify each point with its own subscript to keep them straight. I can then pick any two points to be x0 and x when I use the equations. The t in the kinematic equations refers to the time interval between the two points in the equation, with x0 occurring at the earlier time. I use Δt rather than t to be explicit that this is a time interval (t – t0) and not a point in time.
My book uses “t” rather than “Δt” in the equations. Is that ok?
OrMy book gives more than three equations. Why do you only use these three?
The t in the kinematic equations refers to the time interval between the two points in the equation, with x0 occurring at the earlier time. I use Δt rather than t to be explicit that this is a time interval (t – t0) and not a point in time.
Some text books will give more than three kinematic equations—for example, they may provide “range equations” or different versions of the equations for horizontal and vertical motion. Those are just these three equations solved for special cases. In my view, it is better to know and understand three equations that will always work than to memorize many equations which are specific to certain situations only.Can’t you just use the definition of acceleration for the first question?
Equation 2 is simply the definition of average acceleration (a = Δv/Δt) rewritten. If you recognized that you just have a definition problem in the first question, you saved yourself one step of algebra!
How did you know which point is v and which is v0?
By convention, we choose x0, v0, and t0 to be the earlier (in time) of the two points considered in the equation. With that convention, Δt is positive. Therefore, in this problem, “x” refers to Point 2 and “x0” refers to Point 1.
How did you convert 60 mph into 26.8 m/s?
(60 miles/hour)(1.609 km/mile) = 96.54 km/hour
(96.54 km/hour)(1000 m/km) = 96,540 m/hour
(96,540 m/hour)(1 hour/3600 s) = 26.8 m/s?
Note that in general, the conversion between mph and m/s is (1.609 km/mile)(1000 m/km)(1 hour/3600 s) = 0.447 m/mile hr/s and so you can save steps by just multiplying speed in mph by 0.447 to get speed in m/s.My numbers are close but not exactly what is shown in the equation. Am I close enough?
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution. The answer in this problem is quite sensitive to the stage at which you rounded numbers, so as long as you followed the same procedure don’t worry if your number is a little bit different.
How did you know which point is x and which point is x0?
By convention, we choose x0, v0, and t0 to be the earlier (in time) of the two points considered in the equation. With that convention, Δt is positive. Therefore, in this problem, “x” refers to Point 2 and “x0” refers to Point 1.
Why is acceleration 5.5 m/s2 and not -9.8 m/s2?
The acceleration of the car in this case is 5.5 m/s2. It is true that gravity acts on the car, but it is balanced by the upward force from the road. So the car does not experience an acceleration in the vertical direction. In the kinematic equations, acceleration refers to the actual motion of the object and not to effects that any given force would have if it acted alone.
My numbers are close but not exactly what is shown in the equation. Am I close enough?
Only two significant figures were given in the text of the problem, so only two significant figures are included in the solution.
How do you know x1 and t1 are 0?
All that matters for describing motion is that you explicitly state where your reference points are. In this case, I chose to start the clock and measure distance from the starting point in the problem. No matter what I call x1 and t1, the intervals between them and x2 and t2 will be the same.
My book uses variables like x, x0, v, v0, and t. Why do you use 1 and 2 as subscripts, and Δt instead of t?
The kinematic equations relate position and velocity at any two points in the motion. Because many problems provide or ask about information at more than two points, I identify each point with its own subscript to keep them straight. I can then pick any two points to be x0 and x when I use the equations. The t in the kinematic equations refers to the time interval between the two points in the equation, with x0 occurring at the earlier time. I use Δt rather than t to be explicit that this is a time interval (t – t0) and not a point in time.
-

v2 = v1 + aΔt
26.8 m/s = 0 + a(4.9 s)
5.5 m/s2 = a
In this problem, you were first asked to find the acceleration of the car for the case where it goes from a velocity of 0 to 60 mph in a time of 4.9 s. The answer is a little bit more than half that of gravity (about 0.56g) which is a reasonable answer for the maximum acceleration of a Mustang.
x2 = x1 + v1Δt + ½ a(Δt)2
x2 = 0 + (0) Δt + ½ (5.5 m/s2)(4.9 s)2
x2 = 66 m
In the second part, you were asked to find how far the car traveled in that amount of time, and so the position-time equation gives the answer most directly.
