University of Wisconsin Green Bay

• 
• Problems
• Kinematics

Kinematics (Description of Motion) Problems

Also known as motion problems, these problems ask you to describe motion. Time is a key variable that tells you to work with the kinematic equations. If you are only asked for positions and velocities, you may also be able to work the problem using Conservation of Energy.

How to Solve Kinematic Problems

1. Identify the Problem

Any problem that asks you to describe the motion of an object without worrying about the cause of that motion is a kinematics problem, no matter what was given or requested in the problem. In some cases, you can use either kinematics or energy to solve a problem. However, if you are asked about time or horizontal motion you most likely will need to use kinematics.

2. Draw a Picture:

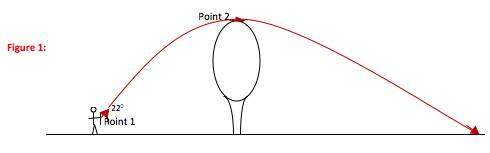
Because kinematic problems focus on describing motion, your picture should be a picture of the motion or path of the object of interest. Make sure to mark key points on the picture (any point about which you are given information, any point about which you are asked for information, and any point such as the top of the motion where you know information (like v_y = 0 at the top of the arc) without being explicitly told. Be careful: you do NOT know that v = 0 when an object reaches the ground. As soon as it touches the ground, there is a new force on it and the problem changes. The kinematic equations you will use are valid only up until the point where the object almost touches down.

In addition to marking key points, you should pick an origin. In other words, pick a location where x = 0 and y = 0. All other position values are then measured from that location.

Finally, kinematic variables (x, v, and a) are vectors, and so you will only be able to work with the equations one direction at a time. It is very easy to forget to work with the correct component while you are in the middle of the problem, so taking a few minutes to divide all vectors into components and organize them in a table will save a lot of mistakes and time in the long run.

3.Select the Relation

There are three key kinematic equations. If you carefully select the equation which most directly describes the situation in your problem, you will not only solve the problem in fewer steps but also understand it better. The three equations, written for motion in the x-direction, are:

1. x = x₀ + v₀Δt + ½ a(Δt)² (relates position and time)
2. v = v₀ + aΔt (relates velocity and time)
3. v² = v₀² + 2a(Δx) (relates velocity and position)

Note that some books give more than three equations. For example, they might reproduce these equations with –g instead of a for motion in the y-direction, or combine them together into a range equation. All of those are special case equations—they are partially solved versions of these three basic equations and only work in certain situations. (The range equation, for example, is only valid if the object lands at the same height from which it was thrown.) It is far better to always start with one of the three basic equations. They always apply and are always used in the same way.

The greatest challenge in kinematic problems is picking the best equation to use to solve your problem. The way to do this is to think about which answer you want. If the problem asks you for position, which position is it? If you want position at a given time, pick equation 1. If you want position at a given velocity, pick equation 2. v₀ and a occur in all equations, and so if you are asked to solve for either of those variables you will need to identify two known quantities and select the equation that relates them.

• 4. Solve the Problem

  The kinematic equations are vector equations and so must be solved in the x- and y-directions separately. For many problems, you will only need to work in one dimension. If you ever need to relate the two (for example if your question asks for an x-position when the object has a given y-position) you need to go through time. Use what you know to solve for time in that direction, then use time in the other direction for your desired information.

  The only tricky algebra in kinematics is if you need to solve equation 1 when v₀ is not equal to zero. In that case, you will need to use the quadratic equation.

  The quadratic equation is of the form aΔt² + bΔt + c = 0, and is solved by

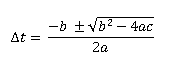
• 5. Understand the Results

  Once you have completed the problem, look at it again. Does your answer make sense? Did it give the behavior you intuitively expected to find? Can you now do steps that caused you problems earlier or do a better job identifying which equation is best to use? Can you explain in words what is happening? If you only recognized it as a kinematics problem because of the section heading in your text book, identify the information that you would use to recognize a problem like this on the final exam.

Help! I can’t find an example that looks like the problem I need to work!

• Are you certain your problem is a kinematics problem?

  A common mistake is to think too hard. If you are told distance and asked for average velocity, or vice versa, the two are directly related through just the definition of average velocity. Check Definition and Ratio problems to see if you can find a useful example.

  It is also possible that your problem is better solved using energy and momentum. There is a lot of overlap between kinematics and energy problems, so check Energy and Momentum problems to see if you can find a useful example there.

• Yes, my problem is definitely a kinematics problem.

  In that case, think more broadly about what makes a useful example. Remember, you were given your assignment to practice the problem solving approach, not because the answers to your problems are particularly interesting. An example in which you merely substitute your numbers for those in the problem will give you practice entering numbers on your calculator but will teach you nothing about physics, and when you take your exam every problem on it will feel new and different to you. So think about your example as support for helping you to practice the problem solving approach.

  And every single problem in this section uses the very same approach, so any problem is an appropriate example to help you approach your problem. It isn’t the way a problem looks that determines how you solve it, it is the type of problem (in this case, kinematics) that you need to consider. That said, different situations require you to do different side problems along the way. If you are asked for time you might need to solve the quadratic equation, and if the problem is two dimensional you might need to go between the x- and y-directions. So if your problem has any of these features, you may find it useful to pick an example that does as well. But don’t worry, you don’t need (or want) an example to look exactly like your problem!