You have designed a merry-go-round with nearly perfect bearings so that it rotates with virtually no friction. If you wanted to apply a constant force of 180 N to the merry-go-round as you ran around the outside, how fast would you have to run after 5.0 s? The radius of your merry-go-round is 1.8 m and its mass of 32 kg is uniformly distributed.
-
In this problem, you are asked to related the kinematic (description of motion) variable velocity to the cause of motion-a dynamic variable. In other words, this is a two part problem. Kinematics and dynamics are linked through acceleration, and so you will work a dynamics problem relating the cause and effect of the motion (force and acceleration) and then you can use the acceleration in a kinematics problem to describe the motion.
Do not worry if you don't recognize both parts of the problem at this point. If you recognize the dynamics problem, you will solve for angular acceleration. At that point, you will see that you are not yet done and need to do another step to find velocity. On the other hand, if you recognize this as a kinematics problem you will quickly see that you need to find angular acceleration before you can begin and so will need to do that pre-step first.
Finally note that in this problem you and the merry-go-round are moving around. In other words, this is an angular motion problem. You can always relate angular and linear variables through the definition of the angular variable.
Regardless of whether you are looking at angular or linear problems, the forces on a system determine the acceleration of the system. All kinematic equations require you to know acceleration order to solve for other variables of motion. So acceleration appears in both dynamics and kinematics problems.
It doesn't matter that the system of interest is spinning around-when you relate either linear or angular descriptive variables and time, you can understand the motion through kinematics.
Because the system of interest in this problem (the merry-go-round) is spinning around, you will work the force and kinematics portions of the problems for angular motion. This means that you will use forces to find torque, and torque is related to angular acceleration.
Don't worry that the problem asks you for linear velocity and you will work this as an angular motion problem. Once you solve the kinematic equations to find angular velocity, you can relate it to linear velocity through the definition of angular velocity (ω = v/r).
Angular dynamics problems are worked through torque. Angular description of motion problems are worked through the angular kinematic equations. In both cases, note that the angular equations are of exactly the same form as, and worked very similarly to, the linear equations-just substitute the angular variable for the corresponding linear variable in the equation.
In this problem, you know about the cause of motion of the merry-go-round and so the merry-go-round is the system of interest. Because it is rotating, you will work with rotational kinematics and dynamics.
I'm told about force and asked about velocity. How do I begin?
This will be a two part problem. Force, the cause of motion, can always be related to descriptive variables such as velocity through acceleration.
Is this an angular or linear problem?
Because you know about forces on the merry-go-round, the merry-go-round is the system you need to understand while working this problem. The merry-go-round is spinning. Therefore, it is a rotational motion problem.
-
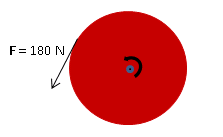
The object whose motion you are understanding is the merry-go-round, and the merry-go-round is rotating. And effective picture for solving dynamics problems in the case of rotational motion shows not only the forces on the object of interest but also their location, and also identifies the axis of rotation.
Why did you focus the picture on the merry-go-round and not on you? The question asks for your velocity.
It is true that you want to know about your velocity. However, you and the merry-go-round move together. In this case, you have information about the cause of the merry-go-round's motion but you do not have information about the forces on you.
Why did you show only one force on the merry-go-round?
Other forces present--such as gravity and the support of the axle--do not act to rotate the merry-go-round. If you do not see that at this stage, it is perfectly find to put them in. When you fill in for torque, you will see that they do not contribute.
It is true that you want to know about your velocity. However, you and the merry-go-round move together. In this case, you have information about the cause of the merry-go-round's motion but you do not have information about the forces on you.
You put a force on the merry-go-round as you push it. Because you are on the outside of the merry-go-round, it is reasonable to assume that your force is located at the outer edge. In addition, you are most likely pushing in the direction of your motion although that was not explicitly stated.
In this case, the merry-go-round spins around a central axis and so that is the clear choice for the axis of rotation.
-
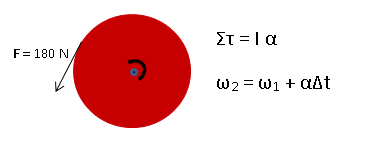
In one part of this problem, you will relate the cause of motion to its effect. Just as you would use ΣF = ma for a linear problem, you add torques to find angular acceleration in a rotational problem.
Once you know angular acceleration, you can use it to describe the motion. In this problem you want to know velocity after a certain amount of time. In other words, you want the velocity-time relationship for angular motion.
Why did you use the rotational formulas? You are given and asked for linear variables.
You always work problems according to the physics of the situation. In this case, you and the merry-go-round are moving around. You can always relate linear and rotational variables through the definition of the rotational variables, and so it doesn't matter what you are given. As always, focus on the physics.
How did you know which rotational kinematic formula to use?
There are three key kinematic formulas--one that relates position and time, one that relates velocity and time, and one that relates velocity and position. It does not matter what you are asked, focus on the situation. In this case, you are asked to examine velocity at a given time. Because the motion is rotational, I used the rotational version of the velocity-time formula.
When forces act to cause circular motion, we understand the motion through torque. Every force puts a torque on the object--larger forces, forces further from the axis of rotation, and forces directed perpendicular to the radius have the greatest effect as shown by the definition of torque: τ = F r sinθ. So even though we were told about force in the problem, the rotational effects of force are understood through torque.
Because the motion in this situation is rotational, we need to understand the problem through rotational kinematics and rotational dynamics. It is fine that the answer requests a linear quantity (velocity.) Velocity and angular velocity (ω) are related through the definition of angular velocity (ω = v/r).
Angular acceleration is labeled by the symbol α and is defined by α = a/r.
There are three key kinematic formulas--one that relates position and time, one that relates velocity and time, and one that relates velocity and position. It does not matter what you are asked, focus on the situation. In this case, you are asked to examine velocity at a given time. Because the motion is rotational, I used the rotational version of the velocity-time formula.
The angular kinematic equations relate angular position and angular velocity at any two points in the motion. Because many problems provide or ask about information at more than two points, I identify each point with its own subscript to keep them straight. I can then pick any two points to be θ0 and θ when I use the equations. The t in the kinematic equations refers to the time interval between the two points in the equation, with t0 occurring at the earlier time. I use Δt rather than t to be explicit that this is a time interval (t - t0) and not a point in time.
-
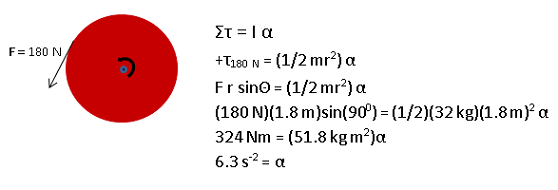
Now that you have found the angular acceleration, you can proceed to the original question--to find your velocity after 5.0 s. If you had not originally recognized that you would need to do this pre-step, you may have started with the kinematics. You would quickly realize that you needed a to solve the problem and so would have done this as a side step at that point.
What do you mean by s-2?
Dimensional analysis for this problem results in a strange unit. Remember that radians are unitless, and rotational problems are worked in radians. So this really represents an angular acceleration in radians/s2.
The direction of torque is always perpendicular to the plane in which the force acts. Direction of torque can be found by the right hand rule. The easiest way to use the right hand rule is to to determine which direction the object would rotate under only the influence of the torque whose direction you want to find. Curl the fingers of your right hand in the direction of the rotation. If your thumb points up, that torque is +. If it points down, it is -.
I always list a torque term due to every force, along with its correct sign, as an intermediate step before I calculate the size of the torques. That way I am sure not to miss any terms, and I focus carefully on direction. If you had included forces such as gravity and a force due to the axis on your drawing, you would list them here as well. You would run into a problem determining the direction of those torques--that would be a cue to you to consider that they might be 0. In this case, those torques are indeed 0 because those forces act at r=0.
The effect that a given net torque can have depends on the mass of the object and on how that mass is distributed. The dependence is reflected by the use of the moment of inertia, I, rather than the mass of the object. You can look up the moment of inertia for different shapes (different distributions of mass) in your text or on line. In this case, I treated the merry-go-round as a disk.
Torque is given the symbol τ and defined by τ = F r sinθ. F is the force that produces the torque, r is the straight line distance from the axis of rotation to the place the force acts, and θ is the angle between F and r.
In this problem, F acts along the tangent to the circle and r is along the radius, so the angle between the two vectors is 900.
N m = (kg m/s2)(m) = (kg m2/s2). Therefore, (N m)/(kg m2) = (kg m2/s2)/(kg m2) = s-2.
This dimensional analysis results in a strange unit. Remember that radians are unitless, and rotational problems are worked in radians. So this really represents an angular acceleration in radians/s2.
----------------------------------------------------------------------------------------------
Step 2
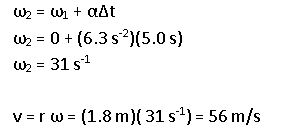
Once you know angular acceleration, it is straightforward to find your final angular velocity. Because you are asked for linear velocity, you need to use the definition of angular velocity to relate the two.
How do you know the system starts from rest?
I don't know for sure. But if I think about pushing a merry-go-round to make it spin, I would typically begin pushing from a stop and nothing in the problem suggests otherwise. In any case, there is no other initial velocity given or implied.
Angular velocity, ω, is defined as ω = v/r.
If I think about pushing a merry-go-round to make it spin, I would typically begin pushing from a stop. Nothing in the problem suggests otherwise, and so I took the starting motion to be at rest. In any case, there is no other initial velocity given or implied.
r in the definition of angular velocity refers to the straight line distance between the axis of rotation and the location at which you want to know the velocity. In this case, we want to know your velocity and you push from the outer edge of the merry-go-round.
-

Even though you were told and asked about linear variables, this is a rotational motion problem because the object whose motion you can best understand, the merry-go-round, is rotating. The cause of motion (torque) was used to find the angular acceleration, after which the motion could be described in terms of other variables. As a final step, the rotational velocity can be related to the requested linear velocity.
There is a second consideration to understanding this problem. 56 m/s is too fast to run--125 mph. Can the number be right? 180 N is about 40 pounds of force, so you aren't pushing that hard. But in this case the resulting acceleration is about an additional rotation every second, and in order to keep exerting that constant force, you need to run faster and faster for 5 seconds. A constant acceleration can require you to get faster pretty quickly. The problem suggests that this might not be possible when it asks "how fast would you have to run..."
My book uses variables like θ, θ0, ω, ω0, and t. Why do you use 1 and 2 as subscripts, and Δt instead of t?
The angular kinematic equations relate angular position and angular velocity at any two points in the motion. Because many problems provide or ask about information at more than two points, I identify each point with its own subscript to keep them straight. I can then pick any two points to be θ0 and θ when I use the equations. The t in the kinematic equations refers to the time interval between the two points in the equation, with θ0 occurring at the earlier time. I use Δt rather than t to be explicit that this is a time interval (t - t0) and not a point in time.
Is this an angular or a linear problem? It asks about linear variables but the merry-go-round spins around.
You should always work problems according to the key physics of the situation you are asked to understand. In this case, the merry-go-round spins and your run around it, so it is a circular motion problem. You can always relate angular and linear variables through the definition of the angular variable.
